Как рассчитать ток в трехфазной сети: Калькулятор перевода силы тока в мощность (амперы в киловатты)
Калькулятор перевода силы тока в мощность (амперы в киловатты)
Мощность — энергия, потребляемая нагрузкой от источника в единицу времени (скорость потребления, измеряется в Ватт). Сила тока — количество энергии, прошедшей за величину времени (скорость прохождения, измеряется в амперах).
Мощность численно равна произведению тока, протекающего через нагрузку, и приложенного к ней напряжения.
Чтобы перевести Ватты в Амперы, понадобится формула: I = P / U, где I – это сила тока в амперах; P – мощность в ваттах; U – напряжение у вольтах.
Если сеть трехфазная, то I = P/(√3xU), поскольку нужно учесть напряжение в каждой из фаз. Корень из трех приблизительно равен 1,73. Чтобы перевести ток в мощность (узнать, сколько в 1 ампере ватт), надо применить формулу:
P = I * U или P = √3 * I * U, если расчеты проводятся в 3-х фазной сети 380 V.
Таблица перевода Ампер – Ватт:
220 В |
| ||
100 Ватт | 0,45 | 0,15 | Ампер |
200 Ватт | 0,91 | 0,3 | Ампер |
300 Ватт | 1,36 | 0,46 | Ампер |
400 Ватт | 1,82 | 0,6 | Ампер |
500 Ватт | 2,27 | 0,76 | Ампер |
600 Ватт | 2,73 | 0,91 | Ампер |
700 Ватт | 3,18 | 1,06 | Ампер |
800 Ватт | 3,64 | 1,22 | Ампер |
900 Ватт | 4,09 | 1,37 | Ампер |
1000 Ватт | 4,55 | 1,52 | Ампер |
Допустим, что вы живете в квартире со старым электросчетчиком, и у вас установлена автоматическая пробка на 16 Ампер. Чтобы определить, какую мощность «потянет» пробка, нужно перевести Амперы в киловатты. Для удобства расчетов принимаем cosФ за единицу. Напряжение нам известно – 220 В, ток тоже, давайте переведем: 220*16*1=3520 Ватт или 3,5 киловатта – ровно столько вы можете подключить единовременно.
Чтобы определить, какую мощность «потянет» пробка, нужно перевести Амперы в киловатты. Для удобства расчетов принимаем cosФ за единицу. Напряжение нам известно – 220 В, ток тоже, давайте переведем: 220*16*1=3520 Ватт или 3,5 киловатта – ровно столько вы можете подключить единовременно.
Сложнее дело обстоит с электродвигателями, у них есть такой показатель как коэффициент мощности. Если полная мощность двигателя 5,5 киловатт, то потребляемая активная мощность 5,5*0,87= 4,7 киловатта. Стоит отметить, что при выборе автомата и кабеля для электродвигателя нужно учитывать полную мощность, поэтому нужно брать ток нагрузки, который указан в паспорте к двигателю. И также важно учитывать пусковые токи, так как они значительно превышают рабочий ток двигателя.
Трёхфазный ток, преимущества трёхфазного тока при использовании
Преимущества трёхфазного тока очевидны только специалистам электрикам. Что такое трехфазный ток для обывателя представляется весьма смутно. Давайте развеем неопределенность.
Давайте развеем неопределенность.
Трехфазный переменный ток
Большинство людей, за исключением специалистов — электриков, имеют весьма смутное представление, что такое так называемый «трёхфазный» переменный ток, да и в понятиях, что такое сила тока, напряжение и электрический потенциал, а также мощность, — часто путаются.
Попытаемся простым языком дать начальные понятия об этом. Для этого обратимся к аналогиям. Начнём с простейшей – протекания постоянного тока в проводниках. Его можно сравнить с водным потоком в природе. Вода, как известно, всегда течёт от более высокой точки поверхности к более низкой. Всегда выбирает самый экономичный (наикратчайший) путь. Аналогия с протеканием тока – полнейшая. Причём количество воды протекающей в единицу времени через какое-то сечение потока будет аналогично силе тока в электрической цепи. Высота любой точки русла реки относительно нулевой точки – уровня моря – будет соответствовать электрическому потенциалу любой точки цепи. А разница в высоте любых двух точек реки будет соответствовать напряжению между двумя точками цепи.
А разница в высоте любых двух точек реки будет соответствовать напряжению между двумя точками цепи.
Используя эту аналогию можно легко представить в уме законы протекания постоянного электрического тока в цепи. Чем выше напряжение – перепад высот, тем больше скорость потока, и, следовательно, количество воды протекающей по реке в единицу времени.
Водный поток, точно так же как электрический ток при своём движении испытывает сопротивление русла – по каменистому руслу вода будет протекать бурно, меняя направление, немного нагреваясь от этого (бурные потоки даже в сильные морозы не замерзают вследствие нагрева от сопротивления русла). В гладком канале или трубе вода потечёт быстро и в итоге в единицу времени канал пропустит гораздо больше воды, чем извилистое и каменистое русло. Сопротивление потоку воды полностью аналогично электрическому сопротивлению в цепи.
Теперь представим закрытую бутылку, в которой налито немного воды. Если мы начнём эту бутылку вращать вокруг поперечной оси, то вода в ней будет перетекать попеременно от горлышка к донышку и наоборот.
Откуда вообще появилось понятие переменный ток? к содержанию
Да с тех самых пор, когда человечество, узнав, что перемещение магнита вблизи проводника вызывает электрический ток в проводнике. Именно движение магнита вызывает ток, если магнит положить рядом с проводом и не двигать – никакого тока в проводнике это не вызовет. Далее, мы хотим получить (генерировать) в проводнике ток, чтобы использовать его в дальнейшем для каких-либо целей. Для этого изготовим катушку из медного провода и начнём возле неё двигать магнит. Магнит можно передвигать возле катушки как угодно – двигать по прямой туда-сюда, но, чтобы не двигать магнит руками, создать такой механизм технически сложнее, чем просто начать его вращать около катушки, аналогично вращению бутылки с водой из предыдущего примера. Вот именно таким образом — по техническим причинам — мы и получили синусоидальный переменный ток, используемый ныне повсеместно.
В дальнейшем оказалось, что законы протекания переменного тока в цепи отличаются от протекания постоянного тока. Например, для протекания постоянного тока сопротивление катушки равно просто омическому сопротивлению проводов. А для переменного тока – сопротивление катушки из проводов значительно увеличивается из-за появления, так называемого индуктивного сопротивления. Постоянный ток через заряженный конденсатор не проходит, для него конденсатор – разрыв цепи. А переменный ток способен свободно протекать через конденсатор с некоторым сопротивлением. Далее выяснилось, что переменный ток может быть преобразован с помощью трансформаторов в переменный ток с другими напряжением или силой тока. Постоянный ток такой трансформации не поддаётся и, если мы включим любой трансформатор в сеть постоянного тока (что делать категорически нельзя), то он неизбежно сгорит, так как постоянному току будет сопротивляться только омическое сопротивление провода, которое делается как можно меньше, и через первичную обмотку потечёт большой ток в режиме короткого замыкания.
Заметим также, что электродвигатели могут быть созданы для работы и от постоянного тока, и от переменного тока. Но разница между ними такая – электродвигатели постоянного тока сложнее в изготовлении, но зато позволяют плавно изменять скорость вращения обычным регулирующим силу тока реостатом. А электродвигатели переменного тока гораздо проще и дешевле в изготовлении, но вращаются только с одной, обусловленной конструкцией скоростью. Поэтому в практике широко применяются и те, и другие. В зависимости от назначения. Для целей управления и регулирования применяются двигатели постоянного тока, а в качестве силовых установок – двигатели переменного тока.
Далее конструкторская мысль изобретателя генератора двигалась примерно в таком направлении – если удобнее всего для генерации тока использовать вращение магнита рядом с катушкой, то почему бы вместо одной катушки генератора не расположить вокруг вращающегося магнита несколько катушек (места-то вокруг вон сколько)?
Получится сразу же, как бы несколько генераторов, работающих от одного вращающегося магнита. Причём переменный ток в катушках будет отличаться по фазе – максимум тока в последующих катушках будет несколько запаздывать относительно предыдущих. То есть синусоиды тока, если их графически изобразить, будут, как бы между собой, сдвинуты. Это важное свойство – сдвиг фаз, о котором мы расскажем ниже.
Причём переменный ток в катушках будет отличаться по фазе – максимум тока в последующих катушках будет несколько запаздывать относительно предыдущих. То есть синусоиды тока, если их графически изобразить, будут, как бы между собой, сдвинуты. Это важное свойство – сдвиг фаз, о котором мы расскажем ниже.
Примерно так рассуждая, американский изобретатель Никола Тесла и изобрёл сначала переменный ток, а затем и трёхфазную систему генерации тока с шестью проводами. Он расположил три катушки вокруг магнита на равном расстоянии под углами 120 градусов, если за центр углов принять ось вращения магнита.
(Число катушек (фаз) вообще-то может быть любым, но для получения всех тех преимуществ, что даёт многофазная система генерации тока, минимально достаточно трёх).
Далее русский учёный электротехник Михаил Осипович Доливо-Добровольский развил изобретение Н. Тесла, впервые предложив трёх — и четырёхпроводную систему передачи трёхфазного переменного тока. Он предложил соединить один конец всех трёх обмоток генератора в одну точку и передавать электроэнергию всего по четырём проводам.
По этой же самой причине (сдвиг фаз на 120 градусов) трехфазные трансформаторы получились значительно менее материалоёмкими, так как в магнитопроводе трансформатора происходит взаимопоглощение магнитных потоков и его можно делать с меньшим сечением.
Сегодня трёхфазная система электроснабжения осуществляется четырьмя проводами, три из них называются фазными и обозначаются латинскими буквами: на генераторе — А, В и С, у потребителя — L1, L2 и L3. Нулевой провод так и обозначается – 0.
Нулевой провод так и обозначается – 0.
Напряжение между нулевым проводом и любым из фазных проводов называется – фазным и составляет в сетях потребителей – 220 вольт.
Между фазными проводами тоже существует напряжение, причём значительно выше, чем фазное напряжение. Это напряжение называется линейным и составляет в цепях потребителей 380 вольт. Почему же оно больше фазного? Да всё это из-за сдвига фаз на 120 градусов. Поэтому, если на одном проводе, к примеру, в данный момент времени потенциал равен плюс 200 вольт, то на другом фазном проводе в этот же момент времени потенциал будет минус 180 вольт. Напряжение – это разность потенциалов, то есть оно будет + 200 – (-180)=+380 В.
Возникает вопрос, если по нулевому проводу ток не протекает, то нельзя ли его вообще убрать. Можно. И мы получим трёхпроводную систему электроснабжения. С соединением потребителей так называемым «треугольником» — между фазными проводами. Однако нужно заметить, что при неравномерной нагрузке в сторонах «треугольника» на генератор будут действовать разрушающие его нагрузки, поэтому данную систему можно применять при огромном количестве потребителей, когда неравномерности нагрузок нивелируются. Передача электроэнергии от больших электростанций при высоких фазных и линейных напряжениях (сотни тысяч вольт) так и осуществляются. Почему же применяется такое высокое напряжение. Ответ простой – чтобы уменьшить потери в проводах на нагрев. Так как нагрев проводов (потери энергии) пропорционален квадрату протекающего тока, то желательно чтобы протекающий ток был минимален. Ну а для передачи необходимой мощности при минимальном токе нужно повышать напряжение. Линии электропередач (ЛЭП) так и обозначаются, к примеру, ЛЭП – 500 – это линия электропередачи под напряжением 500 киловольт.
Передача электроэнергии от больших электростанций при высоких фазных и линейных напряжениях (сотни тысяч вольт) так и осуществляются. Почему же применяется такое высокое напряжение. Ответ простой – чтобы уменьшить потери в проводах на нагрев. Так как нагрев проводов (потери энергии) пропорционален квадрату протекающего тока, то желательно чтобы протекающий ток был минимален. Ну а для передачи необходимой мощности при минимальном токе нужно повышать напряжение. Линии электропередач (ЛЭП) так и обозначаются, к примеру, ЛЭП – 500 – это линия электропередачи под напряжением 500 киловольт.
Кстати потери в проводах ЛЭП можно ещё более снизить, применяя передачу постоянного тока высокого напряжения (перестаёт действовать емкостная составляющая потерь, действующая между проводами), проводились даже такие эксперименты, но широкого распространения пока такая система не получила, видимо вследствие большей экономии в проводах при трёхфазной системе генерации.
Выводы: преимущества трёхфазной системы к содержанию
В заключение статьи подведём итоги, – какие же преимущества даёт трёхфазная система генерации и электроснабжения?
- Экономия на количестве проводов, необходимых для передачи электроэнергии.
 Учитывая немалые расстояния (сотни и тысячи километров) и то, что для проводов используют цветные металлы с малым удельным электрическим сопротивлением, экономия получается весьма существенной.
Учитывая немалые расстояния (сотни и тысячи километров) и то, что для проводов используют цветные металлы с малым удельным электрическим сопротивлением, экономия получается весьма существенной. - Трёхфазные трансформаторы, при равной мощности с однофазными, имеют значительно меньшие размеры магнитопровода. Что позволяет получить существенную экономию.
- Очень важно, что трёхфазная система передачи электроэнергии создаёт при подключении потребителя к трём фазам как бы вращающееся электромагнитное поле. Опять-таки, вследствие сдвига фаз. Это свойство позволило создать чрезвычайно простые и надёжные трёхфазные электродвигатели, у которых нет коллектора, а ротор, по сути, представляет собой простую «болванку» в подшипниках, к которой не нужно подсоединять никакие провода. (На самом деле конструкция короткозамкнутого ротора имеет свои особенности и вовсе не болванка) Это так называемые трёхфазные асинхронные электродвигатели с короткозамкнутым ротором. Очень широко распространённые сегодня в качестве силовых установок.
 Замечательное свойство таких двигателей – это возможность менять направление вращения ротора на обратное простым переключением двух любых фазных проводов.
Замечательное свойство таких двигателей – это возможность менять направление вращения ротора на обратное простым переключением двух любых фазных проводов. - Возможность получения в трёхфазных сетях двух рабочих напряжений. Другими словами менять мощность электродвигателя или нагревательной установки путём простого переключения питающих проводов.
- Возможность значительного уменьшения мерцаний и стробоскопического эффекта светильников на люминисцентных лампах путём размещения в светильнике трёх ламп, питающихся от разных фаз.
Благодаря этим преимуществам трёхфазные системы электроснабжения получили широчайшее распространение в мире.
Калькулятор мощности трехфазного переменного тока • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Однофазный и трехфазный ток
Однофазную сеть можно сравнить с проселочной дорогой — оно не позволяет получить большую мощность. Трехфазную сеть можно сравнить с автомагистралью — она обычно имеется в промышленных зданиях для питания оборудования большой мощности
Установленный на столбе однофазный трансформатор, предназначенный для подачи электроэнергии в индивидуальные жилые дома (Канада)
Термин «фаза» относится к распределению электрической энергии. Для далеких от физики людей однофазную и трехфазную сеть можно сравнить с иллюстрациями выше. Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети.
Для далеких от физики людей однофазную и трехфазную сеть можно сравнить с иллюстрациями выше. Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети.
В однофазной сети используются два или три провода. Всегда имеется один фазный провод и один провод, называемый нейтралью или нулевым проводом. Ток течет между этими двумя проводами. Если однофазная сеть содержит заземляющий провод, то используется трехпроводная сеть. Однофазная сеть хороша в тех случаях, когда типичными нагрузками являются чисто активные потребители, например, традиционные лампы накаливания и электрические обогреватели.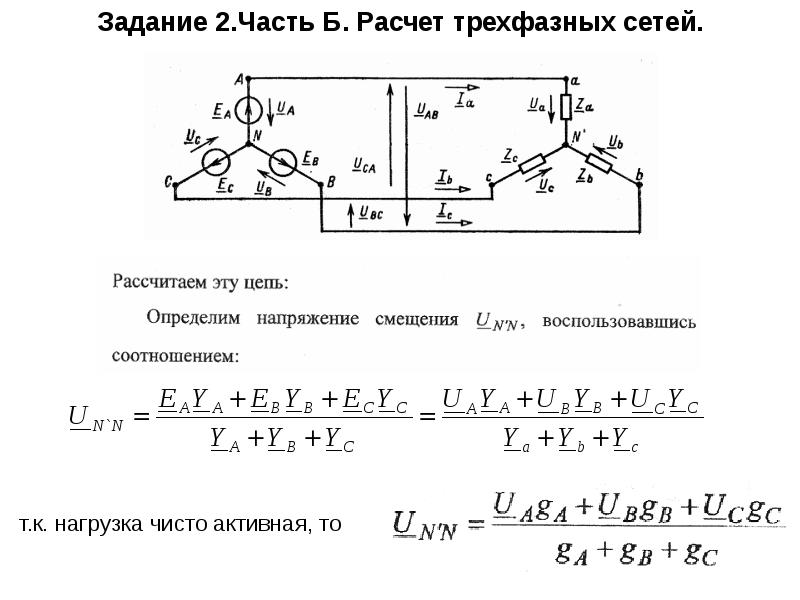 Однофазная система не годится для питания мощных электродвигателей.
Однофазная система не годится для питания мощных электродвигателей.
Установленная на столбе группа из трех трансформаторов, обеспечивающая трехфазное питание небольшой промышленной установки
В трехфазной сети используются три провода, называемые фазными или просто фазами. По этим проводам текут синусоидальные токи со сдвигом фаз относительно друг друга на 120°. В трехфазной системе может быть три или четыре провода. Если имеется четвертый провод, то трехфазную сеть можно использовать для подачи однофазного питания (три линии), например, в индивидуальные жилые дома. При этом от каждой фазы в нагрузку (дом) подается примерно одинаковая мощность. Нейтральный провод часто имеет меньшее сечение, потому что фазные токи взаимно гасятся и по нейтральному проводу обычно течет совсем небольшой ток. Трехфазная система обеспечивает постоянную передачу мощности в нагрузку, что позволяет подключить более высокую нагрузку.
Определения и формулы
Генерация трехфазного тока
В простейшем трехфазном генераторе имеется три идентичных обмотки, расположенных под углом 120° по отношению друг к другу. В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:
В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:
Здесь Up — пиковое значение (амплитуда) напряжения в вольтах, ω — угловая частота в радианах в секунду и t — время в секундах. Напряжение, наведенное в обмотке 2, отстает от напряжения в обмотке 1 на 120°, а напряжение, наведенное в обмотке 3, отстает от напряжения в обмотке 1 на 240°. Ниже на рисунке приведены векторные диаграммы и формы колебаний напряжений генератора:
Если коэффициент мощности равен единице, то в каждой фазе трехфазной системы напряжение, ток и мощность сдвинуты относительно друг друга на 120°; последовательность фаз на этом рисунке U₁, U₂, U₃, потому что U₁ опережает U₂, U₂ опережает U₃, и U₃ опережает U₁.
Преимущества трехфазных систем
- По сравнению с однофазными двигателями, трехфазные двигатели имеют более простую конструкцию, высокий пусковой момент, высокие коэффициент мощности и эффективность, более компактны.

- Передача и распределение трехфазной электроэнергии дешевле в сравнении с однофазной, так как для этого можно использовать провода меньшего сечения при существенном уменьшении стоимости материалов и трудозатрат.
- В отличие от пульсирующей мощности однофазной системы, мгновенная мощность трехфазной системы постоянна, что обеспечивает плавность вращения и отсутствие вибрации двигателей и другого оборудования.
- Размеры трехфазных трансформаторов меньше однофазных трансформаторов аналогичной мощности.
- Трехфазную сеть можно использовать для питания однофазных нагрузок.
- Выпрямление трехфазного тока происходит с меньшей амплитудой пульсаций, по сравнению с выпрямлением однофазного тока.
Последовательность фаз
Последовательность фаз определяется временем, при котором напряжения трех фаз достигают положительного максимума. Последовательность фаз называют также порядком фаз. На рисунке выше последовательность фаз 1-2-3, так как фаза 1 достигает положительного максимума раньше, чем фаза 2, а фаза 3 достигает положительного максимума позже фазы 2. Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.
Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.
Для определения порядка фаз на векторной диаграмме нужно знать, что векторы всегда вращаются против часовой стрелки. Например, на этих трех чертежах последовательность чередования фаз снова U₁, U₂, U₃:
Фазное напряжение и фазный ток
Фазным называется напряжение между каждым из трех фазных проводов и нейтралью. Его также называют напряжением между фазой и нейтралью. Ток, которые течет в нагрузке между фазным проводом и нейтралью, называется фазным током.
Линейное напряжение и ток
Линейным называется напряжение между любыми двумя фазами (линиями). Ток, протекающий в каждой из линий, называется линейным.
Симметричные и несимметричные системы и нагрузки
В сбалансированной (симметричной) трехфазной системе токи во всех трех фазах равны, а сумма всех токов равна нулю, поэтому ток по нейтрали не течет. Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю:
Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю:
То же можно сказать и о токах в симметричной системе:
Если три нагрузки, присоединенные к трем линиям, имеют одинаковую величину и коэффициент мощности, она также называются сбалансированными или симметричными.
Линейные и нелинейные нагрузки
В линейных нагрузках в цепях переменного тока напряжения и токи имеют синусоидальную форму и в любое время ток в нагрузке прямо пропорционален напряжению на ней. Примерами линейных нагрузок являются нагреватели, лампы накаливания. конденсаторы и катушки индуктивности. Все линейные нагрузки подчиняются закону Ома. В линейных нагрузка коэффициент мощности равен cos φ. Подробнее о нелинейных нагрузках — в нашем Калькуляторе активной и реактивной мощности.
В нелинейных нагрузках ток не пропорционален напряжению и содержит гармоники основной частоты 50 или 60 Гц. Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ.
Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ.
Соединение треугольником и звездой
Три обмотки трехфазного генератора можно присоединить к нагрузке шестью проводами, по два на обмотку. Для уменьшения количества проводов обмотки присоединяются к нагрузке тремя или четырьмя проводами. Эти два способа подключения называются треугольником (Δ) и звездой (Y).
В соединении треугольником начало каждой обмотки соединяется с концом следующей обмотки. Таким образом энергию можно передавать только по трем проводам.
Соединение звездой (слева) и треугольником (справа)
В симметричной соединении треугольником напряжения равны по амплитуде, отличаются по фазе на 120° и их сумма равна нулю:
В симметричной четырехпроводной системе соединения звездой с тремя одинаковыми подключенными к каждой фазе нагрузками мгновенное значение тока, текущего по нейтрали, равно сумме трех фазных токов i₁, i₂, и i₃, которые имеют одинаковые амплитуды Ip и сдвинуты по фазе на 120°:
Напряжение и мощность в симметричной трехфазной нагрузке при соединении звездой
Соединение звездой; I₁, I₂, и I₃ — фазные токи, которые равны линейным токам
Полная мощность в трехфазной системе является суммой мощностей, потребляемых нагрузками в каждой из трех фаз. В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна
В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна
Здесь φ — разность фаз между током и напряжением. Поскольку в трехфазном соединении звездой фазное Uph и линейное среднеквадратичное напряжение UL связаны как
а среднеквадратичное значения линейного и фазного токов равны
полная активная мощность определяется следующим уравнением:
Полная реактивная мощность равна
Комплексная мощность:
И, наконец, полная мощность в трех фазах определяется формулой:
Напряжение и мощность в симметричной трехфазной нагрузке при соединении треугольником
Соединение треугольником; I13, I23, и I32 — фазные токи, а I1, I2, и I3 — линейные токи; при этом IL = √3∙Iph
При соединении треугольником нейтральный проводник отсутствует и конец одной обмотки генератора соединяется с началом следующей обмотки. Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать
Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать
При соединении треугольником фазные токи — это токи, текущие через фазные нагрузки. Мы рассматриваем симметричную систему, поэтому фазные среднеквадратичные значения токов Ip1, Ip2 и Ip3 по амплитуде равны (Ip) и отличаются по фазе на 120°:
Как мы уже упоминали, общая мощность в трехфазной системе — это сумма мощностей, потребляемых в нагрузках трех фаз:
где φ — сдвиг фаз между током и напряжением. Поскольку при соединении треугольником среднеквадратичные значения фазного Uph и линейного напряжений UL равны,
а среднеквадратичные значения линейного и фазного токов связаны формулой
активная мощность определяется следующим уравнением:
Полная реактивная мощность равна
Комплексная мощность:
И полная мощность в трех фазах:
Отметим, что приведенные выше уравнения для мощности при соединении звездой и треугольником одинаковые. Мы используем их в этом калькуляторе.
Мы используем их в этом калькуляторе.
То, что эти формулы мощности для звезды и треугольника одинаковые, иногда приводит к ошибочным выводам о том, что можно соединить обмотки одного и того же электродвигателя звездой или треугольником и потребляемая мощность (и ток!) не изменятся. Конечно, это неправильно. И если мы в калькуляторе соединение звездой изменим на треугольник, не изменяя нагрузку, мы увидим, что мощность и потребляемый ток изменятся.
Рассмотрим пример. Трехфазный электродвигатель подключен по схеме треугольника и работает на полной номинальной мощности при линейном напряжении UL и линейном токе IL. Полная мощность в вольт-амперах (ВА) равна
Затем обмотки того же двигателя соединили звездой. Линейное напряжение, приложенное к каждой обмотке, уменьшилось в 1/1,73 раза, при этом сетевое напряжение осталось прежним. Ток в каждой обмотке уменьшился в 1/1,73 раза по сравнению с током, потребляемым при соединении треугольником. Полная мощность также уменьшилась:
Полная мощность также уменьшилась:
Таким образом, полная мощность при соединении звездой равна одной трети мощности при соединении треугольником для нагрузки с тем же импедансом. Очевидно, что полный момент двигателя, обмотки которого соединены звездой, будет в три раза меньше момента того же двигателя при соединении обмоток треугольником.
Иными словами, хотя новая мощность для соединения звездой рассчитывается по той же формуле, что и для треугольника, в расчет нужно вставить другие величины, а именно, напряжение и ток. уменьшенные в 1,73 раза (то есть в квадратный корень из 3).
Расчет симметричной нагрузки по известным напряжению, току и коэффициенту мощности
Для расчета симметричной нагрузки (одинаковой в каждой фазе) по известным напряжению, току и коэффициенту мощности (опережающему или отстающему) используются следующие формулы:
Импеданс нагрузки
ZВ полярной форме:
В комплексной форме:
Расчет тока и мощности по известным напряжению и нагрузке
Фазный ток
По закону Ома, имеем:
Преобразование из прямоугольных координат в полярные и наоборот
Для преобразования из прямоугольных координат R, X в полярные координаты |Z|, φ, используйте следующие формулы:
Треугольник импеданса
В этих формулах R всегда положительно, а X положительно для индуктивной нагрузки (ток отстает от напряжения) и отрицательно для емкостной нагрузки (ток опережает напряжение).
Активное
Rph и реактивное Xph сопротивление нагрузкиИмпеданс конденсатора и катушки индуктивности
Параллельная нагрузка RLC
Параллельное соединение RLC
Для расчета используйте наш Калькулятор импеданса параллельной RLC-цепи.
Последовательная нагрузка RLC
Последовательное соединение RLC
Для расчета используйте наш Калькулятор импеданса последовательной RLC-цепи
Более подробную информацию о нагрузки в форме RLC-цепи вы найдете в наших калькуляторах для расчета импеданса:
Примеры расчетов
Пример 1. Расчет мощности и тока по заданным напряжению и нагрузке
Индуктивная нагрузка из трех цепей с равными импедансами Zph = 5+j3 Ом подключена звездой к трехфазной сети с линейным напряжением 400 В 50 Гц. Рассчитать фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности.
Пример 2. Расчет мощности и тока по заданным напряжению и нагрузке
Индуктивная нагрузка из трех цепей с равными импедансами Zph = 15 ∠60° Ом подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 110 В 50 Гц. Определить тип нагрузки (емкостная или индуктивная) фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности.
Пример 3. Расчет мощности и тока по заданным напряжению и нагрузке
Индуктивная нагрузка из трех обмоток с равными импедансами и эквивалентной схемой в виде включенных последовательно сопротивления Rph = 20 Ом и индуктивности Lph = 440 мГн подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 230 В 50 Гц. Рассчитайте фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Найти линейный ток и потребляемую мощность для той же нагрузки, но соединенной треугольником. Совет: Для определения импеданса каждой обмотки воспользуйтесь Калькулятором последовательной RL-цепи.
Найти линейный ток и потребляемую мощность для той же нагрузки, но соединенной треугольником. Совет: Для определения импеданса каждой обмотки воспользуйтесь Калькулятором последовательной RL-цепи.
Пример 4. Расчет мощности и нагрузки по заданным напряжению и току
Симметричный трехфазный генератор подает фазное напряжение 230 В на включенную звездой нагрузку с отстающим (активно-индуктивным) коэффициентом мощности 0,75. Ток в каждой фазе равен 28,5 А. Рассчитать импеданс нагрузки, активное и реактивное сопротивление в каждой фазе. Также рассчитать полную, активную и реактивную мощности. Описать что произойдет, если для той же нагрузки изменить соединение со звезды на треугольник. Совет: используйте режим определения мощности и нагрузки по заданным току и напряжению, а затем для ответа на последний вопрос воспользуйтесь этим же калькулятором в режиме определения мощности и тока по заданным напряжению и нагрузке.
Пример 5. Расчет мощности и тока по заданным напряжению и нагрузке
Нагрузка, состоящая из трех одинаковых обмоток, имеющих сопротивление Rph = 10 Ом и индуктивность Lph = 310 мГн, подключена треугольником к трехфазной сети с напряжением между фазой и нейтралью 120 В, 60 Гц. Рассчитайте линейное напряжение UL, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор.
Рассчитайте линейное напряжение UL, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор.
Пример 6. Расчет мощности и тока по заданным напряжению и нагрузке
Нагрузка из трех цепей с равными импедансами Zph = 7 – j5 Ом подключена треугольником к трехфазной сети с линейным напряжением (между двумя фазами) 208 В 60 Гц. Определить тип нагрузки (резистивно-емкостная или резистивно-индуктивная) фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности.
Пример 7. Расчет мощности и нагрузки по заданным напряжению и току
Симметричная нагрузка подключена звездой к симметричному трехфазному генератору с линейным (между двумя фазами) напряжением 208 В 60 Гц. В каждом фазном проводе протекает ток Iph = 20 А с запаздыванием относительно напряжения на 15°. Определите фазное напряжение, импеданс нагрузки в каждой фазе в полярной и комплексной форме, активную и реактивную мощности.
Автор статьи: Анатолий Золотков
Как рассчитать максимальную силу переменного тока на входе
Как рассчитать максимальную силу переменного тока на входе
УП-21
Знать максимальный входной ток источника питания полезно при выборе требований к электросети, аварийного выключателя, кабеля питания переменного тока, разъемов и даже изолирующего трансформатора в плавучих блоках. Рассчитать максимальную силу входного тока довольно просто, зная несколько основных параметров и простых математических действий.
Номинальная мощность источника питания высокого напряжения
Для всех источников питания компании Spellman указана номинальная максимальная мощность в ваттах. Это первый нужный нам параметр; получить его можно из техпаспорта изделия. У большей части источников питания компании Spellman максимальная номинальная мощность указана в номере модели. Например, SL30P300/115 — источник питания напряжением 30 кВ с положительной полярностью и максимальной мощностью 300 Вт, работающий от входного напряжения переменного тока 115 В.
КПД источника питания
КПД источника питания — отношение мощности на входе к мощности на выходе. КПД обычно указывается в процентном виде или в виде десятичной дроби меньше 1, например, 80 % или 0,8. Чтобы узнать входную мощность, поделим максимальную выходную мощность на КПД:
300 Вт / 0,8 = 375 Вт
Коэффициент мощности
Коэффициент мощности — отношение реальной мощности к фиксируемой. Обычно он выражается в виде десятичной дроби меньше 1. Реальная мощность указывается в ваттах, а фиксируемая — в вольт-амперах (ВА). У однофазных импульсных источников питания без коррекции коэффициент мощности обычно довольно низок, например, 0,65. Импульсные источники питания без коррекции обладают более высоким коэффициентом мощности, например, 0,85. Блоки питания с активной коррекцией коэффициента мощности могут обладать очень высоким коэффициентом мощности, к примеру, 0,98. В приведенном выше примере используется источник питания без коррекции с питанием от однофазной линии, таким образом:
Реальная мощность указывается в ваттах, а фиксируемая — в вольт-амперах (ВА). У однофазных импульсных источников питания без коррекции коэффициент мощности обычно довольно низок, например, 0,65. Импульсные источники питания без коррекции обладают более высоким коэффициентом мощности, например, 0,85. Блоки питания с активной коррекцией коэффициента мощности могут обладать очень высоким коэффициентом мощности, к примеру, 0,98. В приведенном выше примере используется источник питания без коррекции с питанием от однофазной линии, таким образом:
375 Вт / 0,65 = 577 ВА
Напряжение на входе
Нам необходимо знать входное напряжение переменного тока, для которого предназначен источник питания. В приведенном выше примере оно составляет 115 В. Это номинальное напряжение, в реальности оно указывается с допуском ±10 %. Чтобы предусмотреть наихудший случай с низким напряжением в сети, отнимем 10 %:
115 В – 10 % = 103,5 В
Максимальная сила переменного тока на входе
Взяв 577 ВА и разделив ее на 103,5 В, получаем:
577 ВА / 103,5 В = 5,57 А
Если напряжение на входе однофазное, наш ответ — 5,57 А.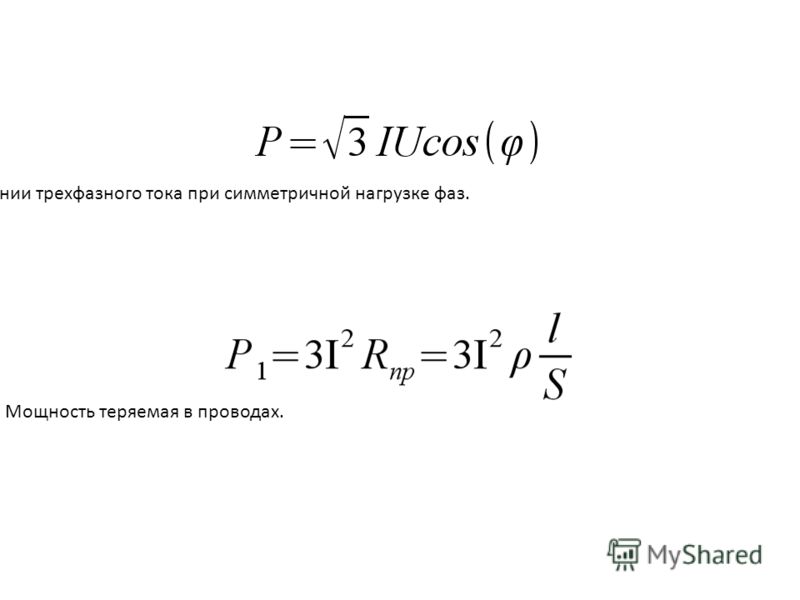
Трехфазное входное напряжение
Источники питания с трехфазным напряжением на входе обладают более высоким коэффициент мощности, чем однофазные. Кроме того, по причине наличия трех фаз, питающих источник, фазовая сила тока будет меньшей. Чтобы узнать силу тока одной фазы, поделим рассчитанную нами силу тока на входе на √3 (1,73).
Рассчитаем данные для следующего примера: STR10N6/208. Из технического паспорта STR узнаем, что максимальная мощность — 6000 Вт, КПД 90 %, а коэффициент мощности 0,85. И хотя STR в силу своей конструкции будет работать с напряжением до 180 В переменного тока, в данном примере его питание будет поступать от трехфазной сети 208 В. Максимальную силу входного тока на одну фазу получаем следующим образом:
КПД источника питания:
6000 Вт / 0,9 = 6666 Вт
Коэффициент мощности:
6666 Вт / 0,85 = 7843 ВА
Напряжение на входе:
208 В – 10 % = 187 В
Максимальная сила переменного тока на входе:
7843 ВА / 187 В = 41,94 А (если бы сеть была однофазной)
Пересчет для трех фаз на входе:
41,94 А / √3 (1,73) = 24,21 А на фазу
Таким образом, у нас есть два уравнения, одно для однофазного и одно для трехфазного напряжения на входе:
Уравнение для максимальной силы однофазного входного тока
Входной ток = максимальная мощность/(КПД)(коэффициент мощности)(максимальное входное напряжение)
Уравнение для максимальной силы трехфазного входного тока
Входной ток = максимальная мощность/(КПД)(коэффициент мощности)(максимальное входное напряжение)(√3)
Данные расчеты входного тока предусматривают наихудший случай, исходя из того, что источник питания работает на максимальной мощности с низким напряжением в линии, а также с учетом КПД и коэффициента мощности.
Как рассчитать ток зная мощность трехфазного двигателя. Какой ток потребляет двигатель из сети при пуске и работе
Идея этого поста родилась после многочисленных доставалок «сильно грамотных» инженеров на тему о том, что на двигатель мощностью, ну например 15 квт надо ставить автомат не ниже 50А, ибо номинал тока 40А + запас на пусковые токи, бла блаблаблабла…Это типичная ошибка тех, кто пытается считать мощность трехфазных асинхронников по стандартной формуле мощности I=P\U, при этом в расчет не берется ни то что двигатель трехфазный, ни то что у него еще есть непонятные почти никому Косинус Фи и КПД.
Кстати при установке новых двигателей ничего и считать не надо, как правило номинальный ток для обоих режимов (звезда 380 и треугольник 220) указан на шильдике, вместе со всеми остальными параметрами.
Так какже, правильно расчитать, грубо или поточнее мощность асинхронного двигателя в стандартной ситуации?
Для начала определимся с это самой «стандартной ситуацией» и с чем ее едят.
Стандартной я называю ситуацию, когда двигатель расчитанный на 380\220 звезда\треугольник, подключается на стандартные 380 звездой, на все три фазы. В промышленности это встречается наиболее часто, и также часто вызывает вопросы по поводу того, какого номинала автоматы ставить, ибо многие, знают стандартную формулу мощности I=P\U и почемуто, видимо от большой грамотности или большого ума, от которого горе по Грибоедову, начинают для трехфазной нагрузки применять ее.
А теперь раскрываю секрет, страааашный секрет….
Для расчета защиты маломощных двигателей на 380В, мощностью до 30 квт вполне достаточно умножить мощность ровно на 2, то есть P*2=~In , автомат все равно выбирается ближайший по номиналу в большую сторону, то есть 63А для 30 квт двигателя, имеющего на валу нагрузкой ну скажем турбину вентилятора типа Циклон. Это страаашный, нигде в учебниках не озвученный секретный экспресс-метод грубого расчета силы тока двигателей на 380В…Почему так? Очень просто при U=380В на один КВТ мощности приходится примерно сила тока в 2 Ампера. (Да меня щас побьют теоретики, которые помнят про КПД и Косинус ФИ…Помолчите Господа, пока помолчите, я же сказал, для МАЛОМОЩНЫХ двигателей до 30 квт, а для низких мощностей, зная модельный ряд наших автоматов, эти 2 значения можно и не учитывать, особенно если нагрузка на вал минимальная)
(Да меня щас побьют теоретики, которые помнят про КПД и Косинус ФИ…Помолчите Господа, пока помолчите, я же сказал, для МАЛОМОЩНЫХ двигателей до 30 квт, а для низких мощностей, зная модельный ряд наших автоматов, эти 2 значения можно и не учитывать, особенно если нагрузка на вал минимальная)
А теперь представим типовой двигатель* со следующими параметрами:
P=30 квт
U=380 В
сила тока на шильдике стерлась…
cos φ = 0,85
КПД=0,9
Как найти его силу тока? Если считать так, как советуют и сами считают упрямые «очень умные» горе-инженера, особенно любящие озадачивать этим вопросом на собеседованиях, то получаем цифру в 78,9А, после чего горе-инженера начинают лихорадочно вспоминать про пусковые токи, задумчиво хмурить брови и морщить лбы, а затем не стесняясь требуют поставить автомат минимум на 100А, так как ближайший по номиналу 80А будет выбивать при малейшей попытке запуска офигенными пусковыми токами…И переспорить их очень тяжело, так как все нижеследующее вызывает у умных дяденек бурю эмоций, недержание мочи и кала, разрыв шаблона, и погружение в глубокий транс с причитаниями и маханием корочками тех универов где они учились считать и жить. .
.
Более полная формула, рекомендованная к применению выглядит несколько иначе.
Мощность в квт переводится в ватты, для чего 30*1000=30000 вт
Затем ватты делим на напряжение, затем делим на корень квадратный из 3(1,73), (у нас же ТРИ ФАЗЫ) и получаем примерную силу тока, которую нужно уточнить, поделив дополнительно на cos φ(коэффициент мощности, ибо всякая индуктивная нагрузка имеет и реактивную мощность Q) и затем, уточнить еще раз, поделив при желании на КПД, итак:
30000вт\380в\1,73=45,63 А\0,85=53,6А
Уточняем расчет: 53,6А\0,9 = 59,65А (Кстати программа электрик, считающая по похожей формуле, выдает более точные данные 59,584 А, то есть немного меньше чем мой проверенный временем расчет…то есть расчет довольно точен, а расхождения в десятые и сотые доли ампера в нашем случае никого особо не волнуют, почему — написано ниже)
59,65 Ампер, — почти полное совпадение с первым грубым расчетом, расхождение составляет всего лишь -0,35А, что для выбора автомата защиты не играет никакой роли в данном случае. Ну и какой же автомат выбрать??
Ну и какой же автомат выбрать??
При условии что нагрузка на валу не велика, скажем какая нибудь турбина вентилятора, можно смело ставить ВА 47-29 на 63А фирмы ИЭК, категории С..наиболее часто встречающиеся.
На вопли о пусковых токах могу смело ответить, что 63А пакетник категории В,С,D выдерживает по току превышение 1,13 раза дольше часа и 1,45 раза меньше часа, то есть если на автомате написано 63А, то это не значит, что при броске до 70А его сразу выбьет…Нифига подобного, нагрузку в 113% (сила тока равна 71,19А) он будет держать минимум час, особенно это касается дорогих автоматов фирм Легранд\АВВ, и даже при силе тока в 145% номинала = 91,35А он гарантированно продержит несколько минут, а для раскрута асинхронника и выхода на номинальный режим достаточно нескольких секунд, как правило от 5 до 20 секунд. За это время тепловой расцепитель автомата тупо не успеет разогрется и отключить нагрузку.
Конечно, умные дяди мне сейчас напомнят, что у автомата есть еще электромагнитный расцепитель, и уж он то, ну уж он то точно отрубит при превышении 63А несчастный двигатель. ..Хахаха, хрен вам и горе умное…
..Хахаха, хрен вам и горе умное…
Буковки B,C,D, и некоторые другие в наименовании автомата как раз характеризуют кратность уставки электромагнитного расцепителя, и равна она
В — 3…5
С — 5…10
D — по ГОСТ Р — 10…50, большинство производителей заявляет диапазон 10…20.
Есть более редко встречающиеся
G — 6,4…9,6 (КЭАЗ ВМ40)
K — 8…14
L — 3,2…4,8 (КЭАЗ ВМ40)
Z — 2…3
То есть автомат категории С на 63А гарантированно отключится электромагнитным расцепителем только в диапазоне 315-630А и выше, чего при запуске исправного асинхронника на 30 квт никогда все равно не будет.
Второй законный вопрос- какой провод положить на наш двигатель. Ответ- кабель 4х16 миллиметров квадратных, с лихвой хватит, при длине до 50 метров, при большей длине лучше 25мм выбирать, ибо потери.
Все цифры проверены многократно, лично мной, и экспериментально. Проверены и по выбранным автоматам и по многократным замерам реальной силы тока токовыми клещами.
*-Единственное примечание и уточнение: У старых двигателей советского производства, вновь вводимых в эксплуатацию могут быть меньшие значения косинуса фи и КПД, тогда сила тока может быть чуть выше чем значение грубого расчета. Просто выбирается следующий по номиналу автомат на 80А. Не ошибётесь!
Второе примечание:
Для грубого расчета силы тока двигателя подключенного треугольником к сети 220 через конденсатор, можно взять мощность двигателя в Киловаттах, ну например теже 30 КВТ и умножить примерно на 3,9 и так: 30*3,9=117А
А для расчета конденсатора можно воспользоваться сайтом
В паспорте электрического двигателя указан ток при номинальной нагрузке на валу. Если, например, указано 13,8/8 А, то это означает, что при включении двигателя в сеть 220 В и при номинальной нагрузке ток, потребляемый из сети, будет равен 13,8 А. При включении в сеть 380 В из сети будет потребляться ток 8 А, то есть справедливо равенство мощностей: √ 3 х 380 х 8 = √ 3 х 220 х 13,8.
Зная номинальную мощность двигателя (из паспорта) можно определить его номинальный ток
. При включении двигателя в трехфазную сеть 380 В номинальный ток можно посчитать по следующей формуле:
При включении двигателя в трехфазную сеть 380 В номинальный ток можно посчитать по следующей формуле:
I н = P н/(√3U н х η х сosφ) ,
Рис. 1. Паспорт электрического двигателя. Номинальная мощность 1,5 кВ, номинальный ток при напряжении 380 В — 3,4 А.
Если не известны к.п.д. и коэффициент мощности двигателя, например, при отсутствии на двигателе паспорта-таблички, то номинальный его ток с небольшой погрешностью можно определить по соотношению «два ампера на киловатт», т.е. если номинальная мощность двигателя 10 кВт, то потребляемый им ток будет примерно равен 20 А.
Для указанного на рисунке двигателя это соотношение тоже выполняется (3,4 А ≈ 2 х 1,5). Более точные значения токов при использовании данного соотношения получаются при мощностях двигателей от 3 кВт.
При холостом ходе электродвигателя из сети потребляется незначительный ток (ток холостого хода). При увеличении нагрузки увеличивается и потребляемый ток. С увеличением тока повышается нагрев обмоток. Большая перегрузка приводит к тому, что увеличенный ток вызывает перегрей обмоток двигателя, и возникает опасность обугливания изоляции (сгорания электродвигателя).
Большая перегрузка приводит к тому, что увеличенный ток вызывает перегрей обмоток двигателя, и возникает опасность обугливания изоляции (сгорания электродвигателя).
В момент пуска из сети электрическим двигателем потребляется так называемый пусковой ток
, который может быть в 3 — 8 раз больше номинального. Характер изменения тока представлен на графике (рис. 2, а).
Рис. 2. Характер изменения тока, потребляемого двигателем из сети (а), и влияние большого тока на колебания напряжения в сети (б)
Точное значение пускового тока для каждого конкретного двигателя можно определить зная значение кратности пускового тока — I пуск/I ном. Кратность пускового тока — одна из технических характеристик двигателя, которую можно найти в каталогах. Пусковой ток определяется по следующей формуле: I пуск = I н х (I пуск/I ном). Например, при номинальном токе двигателя 20 А и кратности пускового тока — 6, пусковой ток равен 20 х 6 = 120 А.
Знание реальной величины пускового тока нужно для выбора плавких предохранителей, проверке срабатывания электромагнитных расцепителей во время пуска двигателя при выборе автоматических выключателей и для определения величины снижения напряжения в сети при пуске.
Большой пусковой ток, на который сеть обычно не рассчитана, вызывает значительные снижения напряжения в сети (рис. 2, б).
Если принять сопротивление проводов, идущих от источника до двигателя, равным 0,5 Ом, номинальный ток I н=15 А, а пусковой ток равным пятикратному от номинального, то потери напряжения в проводах в момент пуска составят 0,5 х 75 + 0,5 х 75 = 75 В.
На зажимах двигателя, а также и на зажимах рядом работающих электродвигателей будет 220 — 75 = 145 В. Такое снижение напряжения может вызвать торможение работающих двигателей, что повлечет за собой еще большее увеличение тока в сети и перегорание предохранителей.
В электрических лампах в моменты пуска двигателей уменьшается накал (лампы «мигают»). Поэтому при пуске электродвигателей стремятся уменьшить пусковые токи.
Для уменьшения пускового тока может использоваться схема пуска двигателя с переключением обмоток статора со звезды на треугольник.
При этом фазное напряжение уменьшится в √
З раз и соответственно ограничивается пусковой ток. После достижения ротором некоторой скорости обмотки статора переключаются в схему треугольника и напряжение ни них становится равным номинальному. Переключение обычно производится автоматически с использованием реле времени или тока.
После достижения ротором некоторой скорости обмотки статора переключаются в схему треугольника и напряжение ни них становится равным номинальному. Переключение обычно производится автоматически с использованием реле времени или тока.
Рис. 3. Схема пуска электрического двигателя с переключением обмоток статора со звезды на треугольник
Сумский государственный университет
Расчетно-практическая
работа №1
«Расчет трехфазного асинхронного двигателя
переменного тока»
по предмету «Электротехника»
Группа МВ-81
Вариант 162
Преподаватель Пузько И.Д.
По данным 3-х фазного асинхронного двигателя и заданной схемой соединения обмоток статора определить:
1.
Линейное напряжение питающей трехфазной цепи U л и синхронную частоту вращения поля статора n 0 , номинальную n Н и критическую n КР частоту вращения ротора, номинальную мощность P 1 ном,
потребляемую двигателем из сети, номинальный и пусковой токи двигателя I НОМ и I ПУС, номинальный и максимальный вращающий моменты двигателя М НОМ и М МАХ.
2. Построить кривую зависимости M(S) при U Л = const и определить
кратность пускового момента K п = М пуск /М ном.
3. Построить механическую характеристику n 2 =f(M) при U C =const и определить диапазон частот вращения ротора, при которых возмодна устойчивая работа двигателя.
4. Построить характеристики M(S) и n 2 =f(M) при U 1 =0.9U C =const.
Исходные данные:
Схема соеди-нения | l М =М МАХ / | m 1 =I ПУСК /I НОМ | |||||
голь-ником |
Расчетная часть.
1. При соединении триугольником линейное напряжение составляет 220
В.
2. Синхронная частота вращения поля статора:
3. Номинальная частота вращения ротора:
4. Критическое скольжение:
5. Критическая частота вращения ротора:
6. Номинальная мощность, потребляемая из сети:
7. Номинальный ток двигателя:
9. Пусковой ток двигателя:
10. Номинальный вращательный момент:
11. Маскимальный вращательный момент:
12. Момент при пуске:
13. Кратность пускового момента:
Расчет мощности трехфазного автомата
Для расчета мощности номинала трехфазного автомата необходимо суммировать всю мощность электроприборов, которые будут подключены через него. Например, нагрузка по фазам одинакова:
L1 5000 W + L2 5000 kW + L3 5000W = 15000 W
Полученные ваты переводим в киловатты:
15000 W / 1000 = 15 kW
Полученное число умножаем на 1,52 и получаем рабочий ток А.
15 kW * 1,52 = 22,8 А.
Номинальный ток автомата должен быть больше рабочего. В нашем случае рабочий ток 22,8 А, поэтому мы выбираем автомат 25 А.
Номинал автоматов по току: 6, 10, 16, 20, 25, 32, 40, 50, 63, 80, 100.
Уточняем сечение жил кабеля на соответствие нагрузке здесь.
Данная формула справедлива при одинаковой нагрузке по трем фазам. Если потребление по одной из фаз значительно больше, то номинал автомата подбирается по мощности этой фазы:
Например, нагрузка по фазам: L1 5000 W; L2 4000 W; L3 6000 W.
Ваты переводим в киловатты для чего 6000 W / 1000 = 6 kW.
Теперь определяем рабочий ток по этой фазе 6 kW * 4,55 = 27,3 А.
Номинальный ток автомата должен быть больше рабочего в нашем случае рабочий ток 27,3 А мы выбираем автомат 32 А.
В приведенных формулах 1,52 и 4,55 – коэффициенты пропорциональности для напряжений 380 и 220 В.
Материалы, близкие по теме:
расчет мощности, схема правильного подключения
Не всякому обывателю понятно, что такое электрические цепи. В квартирах они на 99 % однофазные, где ток поступает к потребителю по одному проводу, а возвращается по другому (нулевому). Трехфазная сеть представляет собой систему передачи электрического тока, который течет по трем проводам с возвратом по одному. Здесь обратный провод не перегружен благодаря сдвигу тока по фазе. Электроэнергия вырабатывается генератором, приводимым во вращение внешним приводом.
Увеличение нагрузки в цепи приводит к росту силы тока, проходящего по обмоткам генератора. В результате магнитное поле в большей степени сопротивляется вращению вала привода. Количество оборотов начинает снижаться, и регулятор скорости вращения подает команду на увеличение мощности привода, например путем подачи большего количества топлива к двигателю внутреннего сгорания. Число оборотов восстанавливается, и генерируется больше электроэнергии.
В результате магнитное поле в большей степени сопротивляется вращению вала привода. Количество оборотов начинает снижаться, и регулятор скорости вращения подает команду на увеличение мощности привода, например путем подачи большего количества топлива к двигателю внутреннего сгорания. Число оборотов восстанавливается, и генерируется больше электроэнергии.
Трехфазная система представляет собой 3 цепи с ЭДС одинаковой частоты и сдвигом по фазе 120°.
Особенности подключения питания к частному дому
Многие считают, что трехфазная сеть в доме повышает потребляемую мощность. На самом деле лимит устанавливается электроснабжающей организацией и определяется факторами:
- возможностями поставщика;
- количеством потребителей;
- состоянием линии и оборудования.
Для предупреждения скачков напряжения и перекоса фаз их следует нагружать равномерно. Расчет трехфазной системы получается примерным, поскольку невозможно точно определить, какие приборы в данный момент будут подключены. Наличие импульсных приборов в настоящее время приводит к повышенному энергопотреблению при их пуске.
Наличие импульсных приборов в настоящее время приводит к повышенному энергопотреблению при их пуске.
Распределительный электрощит при трехфазном подключении берется больших размеров, чем при однофазном питании. Возможны варианты с установкой небольшого вводного щитка, а остальных — из пластика на каждую фазу и на надворные постройки.
Подключение к магистрали реализуется по подземному способу и по воздушной линии. Предпочтение отдают последней благодаря небольшому объему работ, низкой стоимости подключения и удобству ремонта.
Сейчас воздушное подключение удобно делать с помощью самонесущего изолированного провода (СИП). Минимальное сечение алюминиевой жилы составляет 16 мм2, чего с большим запасом хватит для частного дома.
СИП крепится на опорах и стене дома с помощью анкерных кронштейнов с зажимами. Соединение с главной воздушной линией и кабелем ввода в электрощит дома производится ответвительными прокалывающими зажимами. Кабель берется с негорючей изоляцией (ВВГнг) и проводится через металлическую трубу, вставленную в стену.
Воздушное подключение трехфазного питания дома
При расстоянии от ближайшей опоры более 15 м необходима установка еще одного столба. Это необходимо для снижения нагрузок, приводящих к провисанию или обрыву проводов.
Высота места присоединения составляет 2,75 м и выше.
Электрораспределительный шкаф
Подключение к трехфазной сети производится по проекту, где внутри дома производится разделение потребителей на группы:
- освещение;
- розетки;
- отдельные мощные приборы.
Одни нагрузки можно отключать для ремонта при работающих других.
Мощность потребителей рассчитывается для каждой группы, где выбирается провод необходимого сечения: 1,5 мм2 — к освещению, 2,5 мм2 — к розеткам и до 4 мм2 — к мощным приборам.
Проводка защищается от короткого замыкания и перегрузки автоматическими выключателями.
Электрический счетчик
При любой схеме подключения необходим прибор учета расхода электроэнергии. 3-фазный счетчик может подключаться непосредственно к сети (прямое включение) или через трансформатор напряжения (полукосвенное), где показания прибора умножаются на коэффициент.
3-фазный счетчик может подключаться непосредственно к сети (прямое включение) или через трансформатор напряжения (полукосвенное), где показания прибора умножаются на коэффициент.
Важно соблюдать порядок подключения, где нечетные номера – это питание, а четные – нагрузка. Цвет проводов указывается в описании, а схема размещается на задней крышке прибора. Вход и соответствующий выход 3-фазного счетчика обозначаются одним цветом. Наиболее распространен порядок присоединения, когда сначала идут фазы, а последний провод – ноль.
3-фазный счетчик прямого включения для дома обычно рассчитан на мощность до 60 кВт.
Перед выбором многотарифной модели следует согласовать вопрос с энергоснабжающей компанией. Современные устройства с тарификаторами дают возможность подсчитывать плату за электроэнергию в зависимости от времени суток, регистрировать и записывать значения мощности во времени.
Температурные показатели приборов выбираются как можно шире. В среднем они составляют от -20 до +50 °С. Срок эксплуатации приборов достигает 40 лет с межповерочным интервалом 5-10 лет.
Срок эксплуатации приборов достигает 40 лет с межповерочным интервалом 5-10 лет.
Счетчик подключается после вводного трех- или четырехполюсного автоматического выключателя.
Трехфазная нагрузка
К потребителям относятся электрокотлы, асинхронные электродвигатели и другие электроприборы. Преимуществом их использования является равномерное распределение нагрузки на каждой фазе. Если трехфазная сеть содержит неравномерно подключенные однофазные мощные нагрузки, это может привести к перекосу фаз. При этом электронные устройства начинают работать со сбоями, а лампы освещения тускло светятся.
Схема подключения трехфазного двигателя к трехфазной сети
Работа трехфазных электродвигателей отличается высокой производительностью и эффективностью. Здесь не требуется наличие дополнительных пусковых устройств. Для нормальной эксплуатации важно правильно подключить устройство и выполнять все рекомендации.
Схема подключения трехфазного двигателя к трехфазной сети создает вращающее магнитное поле тремя обмотками, соединенными звездой или треугольником.
У каждого способа есть свои достоинства и недостатки. Схема звезды позволяет плавно запускать двигатель, но его мощность снижается до 30 %. Эта потеря отсутствует в схеме треугольника, но при пуске токовая нагрузка значительно больше.
У двигателей есть коробка подключения, где находятся выводы обмоток. Если их три, то схема соединяется только звездой. При наличии шести выводов двигатель можно подключить любым способом.
Потребляемая мощность
Для хозяина дома важно знать, сколько потребляется энергии. Это легко подсчитать по всем электроприборам. Сложив все мощности и поделив результат на 1000, получим суммарное потребление, например 10 кВт. Для бытовых электроприборов достаточно одной фазы. Однако потребление тока значительно возрастает в частном доме, где есть мощная техника. На один прибор может приходиться 4-5 кВт.
Важно спланировать потребляемую мощность трехфазной сети на этапе ее проектирования, чтобы обеспечить симметрию по напряжениям и токам.
В дом заходит четырехжильный провод на три фазы и нейтраль. Напряжение электрической сети составляет 380/220 В. Между фазами и нулевым проводом подключаются электроприборы на 220 В. Кроме того, может быть еще трехфазная нагрузка.
Напряжение электрической сети составляет 380/220 В. Между фазами и нулевым проводом подключаются электроприборы на 220 В. Кроме того, может быть еще трехфазная нагрузка.
Расчет мощности трехфазной сети производится по частям. Сначала целесообразно рассчитать чисто трехфазные нагрузки, например электрический котел на 15 кВт и асинхронный электродвигатель на 3 кВт. Суммарная мощность составит P = 15 + 3 = 18 кВт. В фазном проводе при этом протекает ток I = Px1000/(√3xUxcosϕ). Для бытовых электросетей cosϕ = 0,95. Подставив в формулу числовые значения, получим величину тока I = 28,79 А.
Теперь следует определить однофазные нагрузки. Пусть для фаз они составят PA = 1,9 кВт, PB = 1,8 кВт, PC = 2,2 кВт. Смешанная нагрузка определяется суммированием и составляет 23,9 кВт. Максимальный ток будет I = 10,53 А (фаза С). Сложив его с током от трехфазной нагрузки, получим IC = 39,32 А. Токи на остальных фазах составят IB = 37,4 кВт, IA = 37,88 А.
В расчетах мощности трехфазной сети удобно пользоваться таблицами мощности с учетом типа подключения.
По ним удобно подбирать защитные автоматы и определять сечения проводки.
Заключение
При правильном проектировании и обслуживании трехфазная сеть идеально подходит для частного дома. Она позволяет равномерно распределить нагрузку по фазам и подключить дополнительные мощности электропотребителей, если позволяет сечение проводки.
Трехфазный ток — простой расчет
Расчет тока в трехфазной системе был поднят в отзывах на нашем сайте, и это обсуждение, в которое я, кажется, время от времени участвую. Хотя некоторые коллеги предпочитают запоминать формулы или факторы, я предпочитаю решать проблему поэтапно, используя базовые принципы. Я подумал, что неплохо было бы написать, как я делаю эти расчеты. Надеюсь, это может оказаться полезным для кого-то еще.
Трехфазное питание и ток Мощность, потребляемая цепью (одно- или трехфазной), измеряется в ваттах Вт (или кВт). Произведение напряжения и тока представляет собой полную мощность, измеряемую в ВА (или кВА). Соотношение между кВА и кВт — это коэффициент мощности (pf):
Произведение напряжения и тока представляет собой полную мощность, измеряемую в ВА (или кВА). Соотношение между кВА и кВт — это коэффициент мощности (pf):
что также может быть выражено как:
Однофазная система — с этим проще всего иметь дело. Учитывая кВт и коэффициент мощности, можно легко рассчитать кВА. Сила тока — это просто кВА, деленная на напряжение. В качестве примера рассмотрим нагрузку, потребляющую 23 кВт мощности при 230 В и коэффициенте мощности 0.86:
Примечание: вы можете выполнять эти уравнения в ВА, В и А или в кВА, кВ и кА в зависимости от величины параметров, с которыми вы имеете дело. Чтобы преобразовать ВА в кВА, просто разделите на 1000.
Трехфазная система — Основное различие между трехфазной системой и однофазной системой — это напряжение. В трехфазной системе у нас есть линейное напряжение (V LL ) и фазное напряжение (V LN ), связанные следующим образом:
«Введение в трехфазную электрическую мощность».
или как вариант:
чтобы лучше понять это или получить больше информации, вы можете прочитать статью
Для меня самый простой способ решить трехфазные проблемы — это преобразовать их в однофазную.Возьмем трехфазный двигатель (с тремя одинаковыми обмотками), потребляющий заданную кВт. Мощность в кВт на обмотку (однофазная) должна быть разделена на 3. Точно так же трансформатор (с тремя обмотками, каждая из которых идентична), питающий заданную кВА, будет иметь каждую обмотку, обеспечивающую треть общей мощности. Чтобы преобразовать трехфазную задачу в однофазную, возьмите общую мощность в кВт (или кВА) и разделите ее на три.
В качестве примера рассмотрим сбалансированную трехфазную нагрузку, потребляющую 36 кВт при коэффициенте мощности 0.86 и линейное напряжение 400 В (В LL ):
линия к нейтрали (фаза) напряжение В LN = 400 / √3 = 230 В
трехфазная мощность 36 кВт, однофазная мощность = 36/3 = 12 кВт
теперь просто следуйте описанному выше однофазному методу
Достаточно просто. Чтобы найти мощность при заданном токе, умножьте его на напряжение, а затем на коэффициент мощности, чтобы преобразовать его в W. Для трехфазной системы умножьте на три, чтобы получить общую мощность.
Чтобы найти мощность при заданном токе, умножьте его на напряжение, а затем на коэффициент мощности, чтобы преобразовать его в W. Для трехфазной системы умножьте на три, чтобы получить общую мощность.
Использование формулЛичная записка по методу
Как правило, я запоминаю методику (а не формулы) и переделываю ее каждый раз, когда делаю расчет. Когда я пытаюсь запомнить формулы, я всегда быстро их забываю или неуверен, правильно ли я их запоминаю. Мой совет — всегда старайтесь запоминать метод, а не просто запоминать формулы. Конечно, если у вас есть суперспособность запоминать формулы, вы всегда можете придерживаться этого подхода.
Вывод формулы — Пример
Сбалансированная трехфазная система общей мощностью P (Вт), коэффициентом мощности pf и линейным напряжением В LL
Преобразование в однофазную проблему:
P1ph = P3
Полная мощность одной фазы S 1 фаза (ВА):
S1ph = P1phpf = P3 × pf
Фазный ток I (A) — полная мощность одной фазы, деленная на напряжение между фазой и нейтралью (и дано В LN = В LL / √3):
I = S1phVLN = P3 × pf3VLL
Упрощение (и с 3 = √3 x √3):
I = P3 × pf × VLL
Приведенный выше метод основан на запоминании нескольких простых принципов и манипулировании проблемой, чтобы дать ответ.
Для получения того же результата можно использовать более традиционные формулы. Их можно легко получить из вышеприведенного, например:
I = W3 × pf × VLL, дюйм A
Несбалансированные трехфазные системыВышеупомянутое относится к сбалансированным трехфазным системам. То есть ток в каждой фазе одинаковый, и каждая фаза обеспечивает или потребляет одинаковое количество энергии. Это типично для систем передачи энергии, электродвигателей и аналогичного оборудования.
Часто, когда задействованы однофазные нагрузки, например, в жилых и коммерческих помещениях, система может быть несбалансированной, так как каждая фаза имеет разный ток и доставляет или потребляет разное количество энергии.
Сбалансированные напряжения
К счастью, на практике напряжения имеют тенденцию быть фиксированными или очень небольшими. В этой ситуации, немного подумав, можно распространить вышеупомянутый тип расчета на трехфазные системы с несимметричным током. Ключом к этому является то, что сумма мощности в каждой фазе равна общей мощности системы.
Ключом к этому является то, что сумма мощности в каждой фазе равна общей мощности системы.
Например, возьмем трехфазную систему 400 В (V LL ) со следующими нагрузками: фаза 1 = 80 A, фаза 2 = 70 A, фаза 3 = 82 A
линия к нейтрали (фаза) напряжение В LN = 400 / √3 = 230 В
Полная мощность фазы 1 = 80 x 230 = 18400 ВА = 18,4 кВА
Полная мощность фазы 2 = 70 x 230 = 16100 ВА = 16,1 кВА
Полная мощность фазы 3 = 82 x 230 = 18 860 ВА = 18.86 кВА
Общая трехфазная мощность = 18,4 + 16,1 + 18,86 = 53,36 кВА
Аналогичным образом, учитывая мощность в каждой фазе, вы можете легко найти фазные токи. Если вам также известен коэффициент мощности, вы можете преобразовать его из кВА в кВт, как показано ранее.
Несбалансированные напряжения
Если напряжения становятся несимметричными или есть другие соображения (например, несбалансированный фазовый сдвиг), то необходимо вернуться к более традиционному анализу сети. Системные напряжения и токи можно найти, подробно изобразив схему и используя законы Кирхгофа и другие сетевые теоремы.
Системные напряжения и токи можно найти, подробно изобразив схему и используя законы Кирхгофа и другие сетевые теоремы.
КПД и реактивная мощностьСетевой анализ не является целью данной заметки. Если вас интересует введение, вы можете просмотреть наш пост: Теория сети — Введение и обзор
Другие факторы, которые следует учитывать при проведении расчетов, могут включать эффективность оборудования.Зная, что эффективность энергопотребляющего оборудования — это выходная мощность, деленная на входную, опять же, это легко подсчитать. Реактивная мощность не обсуждается в статье, а более подробную информацию можно найти в других примечаниях (просто воспользуйтесь поиском на сайте).
Сводка Помня, что трехфазная мощность (кВт или кВА) просто в три раза больше однофазной мощности, любую трехфазную задачу можно упростить. Разделите кВт на коэффициент мощности, чтобы получить кВА. ВА — это просто ток, умноженный на напряжение, поэтому знание этого и напряжения может дать ток.При вычислении тока используйте фазное напряжение, которое связано с линейным напряжением квадратным корнем из трех. Используя эти правила, можно решить любую трехфазную задачу без необходимости запоминать и / или прибегать к формулам.
ВА — это просто ток, умноженный на напряжение, поэтому знание этого и напряжения может дать ток.При вычислении тока используйте фазное напряжение, которое связано с линейным напряжением квадратным корнем из трех. Используя эти правила, можно решить любую трехфазную задачу без необходимости запоминать и / или прибегать к формулам.
Трехфазная конфигурация Y и треугольника | Полифазные цепи переменного тока
Трехфазное соединение звездой (Y)
Первоначально мы исследовали идею трехфазных систем питания, соединив вместе три источника напряжения в так называемой конфигурации «Y» (или «звезда»).
Эта конфигурация источников напряжения характеризуется общей точкой подключения, соединяющей одну сторону каждого источника. (Рисунок ниже)
Трехфазное соединение «Y» имеет три источника напряжения, подключенных к общей точке.
Если мы нарисуем схему, показывающую, что каждый источник напряжения представляет собой катушку с проводом (генератор переменного тока или обмотку трансформатора), и произведем небольшую перестановку, конфигурация «Y» станет более очевидной на рисунке ниже.
Трехфазное четырехпроводное соединение «Y» использует «общий» четвертый провод.
Три проводника, идущие от источников напряжения (обмоток) к нагрузке, обычно называются линиями , а сами обмотки обычно называются фазами .
В системе с Y-соединением нейтральный провод может быть или не быть (рисунок ниже) в точке соединения посередине, хотя это, безусловно, помогает облегчить потенциальные проблемы, если один из элементов трехфазной нагрузки выйдет из строя, поскольку обсуждалось ранее.
Трехфазное трехпроводное соединение «Y» не использует нейтральный провод.
Значения напряжения и тока в трехфазных системах
Когда мы измеряем напряжение и ток в трехфазных системах, нам нужно уточнить значение , где мы измеряем .
Напряжение сети означает величину напряжения, измеренного между любыми двумя проводниками линии в сбалансированной трехфазной системе. В приведенной выше схеме линейное напряжение составляет примерно 208 вольт.
В приведенной выше схеме линейное напряжение составляет примерно 208 вольт.
Фазное напряжение относится к напряжению, измеренному на любом одном компоненте (обмотка источника или сопротивление нагрузки) в сбалансированном трехфазном источнике или нагрузке.
Для схемы, показанной выше, фазное напряжение составляет 120 вольт. Термины линейный ток и фазный ток следуют той же логике: первый относится к току через любой один линейный проводник, а второй — к току через любой один компонент.
Источники и нагрузки, подключенные по схеме Y, всегда имеют линейные напряжения выше фазных, а линейные токи равны фазным токам.Если источник или нагрузка, подключенные по схеме Y, сбалансированы, линейное напряжение будет равно фазному напряжению, умноженному на квадратный корень из 3:
. Однако конфигурация «Y» не единственная допустимая для соединения трехфазного источника напряжения или элементов нагрузки.
Трехфазная конфигурация, треугольник (Δ)
Другая конфигурация известна как «Дельта» из-за ее геометрического сходства с одноименной греческой буквой (Δ). Обратите внимание на полярность каждой обмотки на рисунке ниже.
Трехфазное, трехпроводное соединение Δ не имеет общего.
На первый взгляд кажется, что три таких источника напряжения могут вызвать короткое замыкание, электроны текут по треугольнику, и ничто, кроме внутреннего сопротивления обмоток, сдерживает их.
Однако из-за фазовых углов этих трех источников напряжения это не так.
Закон Кирхгофа о напряжении в соединении треугольником
Одной из быстрых проверок этого является использование закона Кирхгофа по напряжению, чтобы увидеть, равны ли три напряжения вокруг контура нулю.Если они это сделают, тогда не будет доступного напряжения для проталкивания тока вокруг этого контура и, следовательно, не будет циркулирующего тока.
Начиная с верхней обмотки и двигаясь против часовой стрелки, наше выражение KVL выглядит примерно так:
В самом деле, если мы сложим эти три векторные величины вместе, они в сумме дадут ноль. Другой способ проверить тот факт, что эти три источника напряжения могут быть соединены вместе в петлю без возникновения циркулирующих токов, — это разомкнуть петлю в одной точке соединения и рассчитать напряжение на разрыве: (рисунок ниже)
Напряжение на открытии Δ должно быть нулевым.
Начиная с правой обмотки (120 В ∠ 120 °) и продвигаясь против часовой стрелки, наше уравнение KVL выглядит следующим образом:
Конечно, на разрыве будет нулевое напряжение, что говорит нам о том, что ток не будет циркулировать в треугольной петле обмоток, когда это соединение будет выполнено.
Установив, что трехфазный источник напряжения с Δ-соединением не сгорит до корки из-за циркулирующих токов, перейдем к его практическому использованию в качестве источника питания в трехфазных цепях.
Поскольку каждая пара линейных проводов подключается непосредственно к одной обмотке в цепи Δ, линейное напряжение будет равно фазному напряжению.
И наоборот, поскольку каждый линейный провод присоединяется к узлу между двумя обмотками, линейный ток будет векторной суммой двух соединяющихся фазных токов.
Неудивительно, что результирующие уравнения для Δ-конфигурации выглядят следующим образом:
Анализ цепи примера соединения треугольником
Давайте посмотрим, как это работает на примере схемы: (Рисунок ниже)
Нагрузка на источнике Δ подключена по схеме Δ.
Когда каждое сопротивление нагрузки получает 120 В от соответствующей фазной обмотки источника, ток в каждой фазе этой цепи будет 83,33 А:
Преимущества трехфазной системы Delta
Таким образом, каждый линейный ток в этой трехфазной системе питания равен 144,34 А, что значительно больше, чем линейные токи в системе с Y-соединением, которую мы рассматривали ранее.
Можно задаться вопросом, не потеряли ли мы все преимущества трехфазного питания здесь, учитывая тот факт, что у нас такие большие токи в проводниках, что требует более толстого и более дорогостоящего провода.
Ответ — нет. Хотя для этой схемы потребуется три медных проводника калибра 1 (на расстоянии 1000 футов между источником и нагрузкой это составляет чуть более 750 фунтов меди для всей системы), это все же меньше, чем 1000+ фунтов меди, необходимых для Однофазная система, обеспечивающая одинаковую мощность (30 кВт) при одинаковом напряжении (120 В между проводниками).
Одним из явных преимуществ системы с Δ-соединением является отсутствие нейтрального провода. В системе с Y-соединением нейтральный провод был необходим на случай, если одна из фазных нагрузок выйдет из строя (или отключится), чтобы не допустить изменения фазных напряжений на нагрузке.
Это не обязательно (или даже возможно!) В схеме с Δ-соединением.
Когда каждый элемент фазы нагрузки напрямую подключен к соответствующей обмотке фазы источника, фазное напряжение будет постоянным независимо от обрывов в элементах нагрузки.
Пожалуй, самым большим преимуществом источника с Δ-подключением является его отказоустойчивость.
Возможен отказ одной из обмоток трехфазного источника, подключенного по схеме Δ (рисунок ниже), без влияния на напряжение или ток нагрузки!
Даже при выходе из строя обмотки источника линейное напряжение по-прежнему составляет 120 В, а напряжение фазы нагрузки по-прежнему составляет 120 В. Единственная разница заключается в дополнительном токе в оставшихся функциональных обмотках источника.
Единственным последствием разрыва обмотки источника для источника, подключенного по схеме Δ, является увеличение фазного тока в остальных обмотках. Сравните эту отказоустойчивость с системой с Y-соединением, имеющей обмотку с открытым исходным кодом, как показано на рисунке ниже.
Разомкнутая обмотка источника «Y» снижает вдвое напряжение на двух нагрузках по Δ, подключенных к нагрузке.
При подключении нагрузки по схеме Δ два сопротивления испытывают пониженное напряжение, в то время как одно остается при исходном линейном напряжении, 208. Нагрузка, подключенная по схеме Y, постигает еще худшую судьбу (рисунок ниже) из-за того же отказа обмотки в источнике, подключенном по схеме Y.
Нагрузка, подключенная по схеме Y, постигает еще худшую судьбу (рисунок ниже) из-за того же отказа обмотки в источнике, подключенном по схеме Y.
Обмотка с открытым источником в системе «Y-Y» снижает вдвое напряжение на двух нагрузках и полностью теряет одну нагрузку.
В этом случае два сопротивления нагрузки испытывают пониженное напряжение, а третье полностью теряет напряжение питания! По этой причине источники с Δ-соединением предпочтительнее для надежности.
Однако, если требуется двойное напряжение (например,г. 120/208) или предпочтительнее для более низких линейных токов, предпочтительной конфигурацией являются системы с Y-соединением.
ОБЗОР:
- Проводники, подключенные к трем точкам трехфазного источника или нагрузки, называются линиями .
- Три компонента, составляющие трехфазный источник или нагрузку, называются фазами .
- Напряжение линии — это напряжение, измеренное между любыми двумя линиями в трехфазной цепи.

- Фазное напряжение — это напряжение, измеренное на отдельном компоненте трехфазного источника или нагрузки.
- Линейный ток — это ток через любую линию между трехфазным источником и нагрузкой.
- Фазный ток — это ток через любой компонент, содержащий трехфазный источник или нагрузку.
- В симметричных Y-цепях линейное напряжение равно фазному напряжению, умноженному на квадратный корень из 3, а линейный ток равен фазному току.
- В симметричных схемах Δ линейное напряжение равно фазному напряжению, а линейный ток равен фазному току, умноженному на квадратный корень из 3.
- Трехфазные источники напряжения с Δ-соединением обеспечивают большую надежность в случае выхода из строя обмотки, чем источники с соединением по схеме Y. Однако источники, подключенные по схеме Y, могут выдавать такое же количество энергии при меньшем линейном токе, чем источники, подключенные по схеме Δ.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Еще раз о расчетах трехфазного переменного тока — Dataforth
Преамбула
Это примечание по применению является продолжением публикации Dataforth Указания по применению AN109, которые содержат систему переменного тока определения и основные правила расчетов с примерами.Читателю предлагается ознакомиться с AN109, Ссылки 3, 4 и 5 в качестве фона для данной инструкции по применению.Трехфазная система напряжения
Системы трехфазного напряжения состоят из трех синусоидальные напряжения равной величины, равной частоты и разделены на 120 градусов.На рисунке 1 показаны функции косинуса в реальном времени и соответствующее обозначение вектора для трехфазного межфазного система напряжения с линейным напряжением V12 в качестве эталона.
Обзор свойств системы трехфазного напряжения
Трехфазные сети питания и нагрузки имеют два базовые комплектации; 4-проводная звезда и 3-проводная «Дельта». На рисунке 2 показан базовый трехфазный четырехпроводной звездой.
сконфигурированная система напряжения с V1N в качестве эталона и
На рисунке 3 показана трехпроводная система напряжения, настроенная по схеме «треугольник».
с V12 в качестве ссылки соответственно.
На рисунке 2 показан базовый трехфазный четырехпроводной звездой.
сконфигурированная система напряжения с V1N в качестве эталона и
На рисунке 3 показана трехпроводная система напряжения, настроенная по схеме «треугольник».
с V12 в качестве ссылки соответственно.Важные определения, условные обозначения и правила расчета как для 3-фазной 4-проводной схемы «звезда», так и для 3-проводной схемы «треугольник» сконфигурированные системы напряжения описаны в следующих список без «беспорядочной» векторной математики.
Ориентация фазора:
По определению, все синусоидальные векторы вращаются в
против часовой стрелки с {1-2-3} или {3-2-1}
последовательность и углы измеряются как положительные в
против часовой стрелки.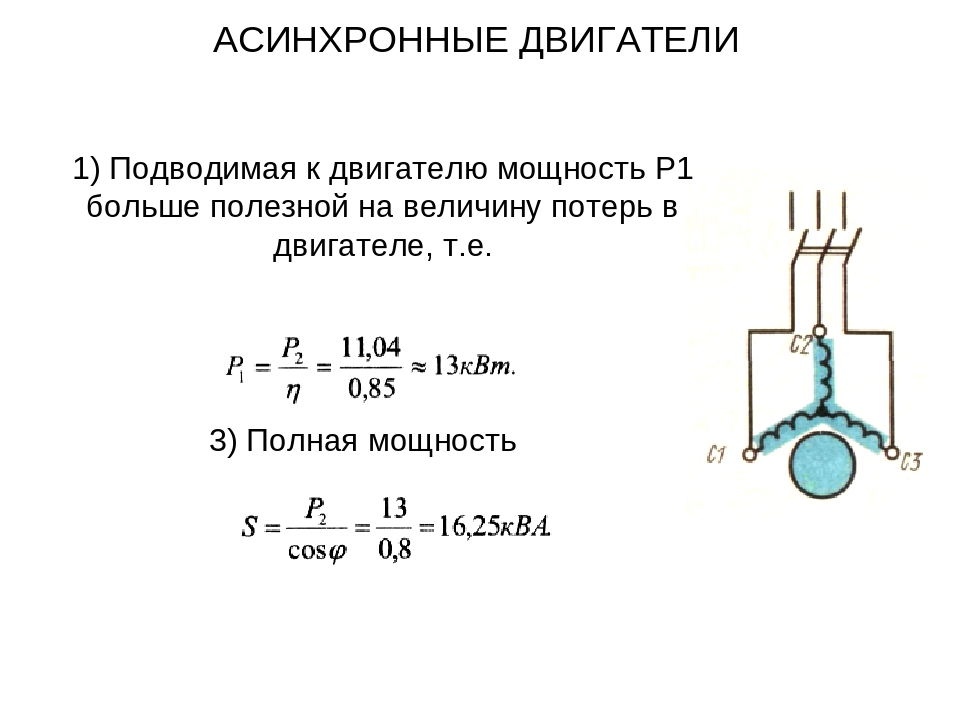 4-проводная 3-фазная система звезды
показан на рисунке 2 с V1N, выбранным в качестве эталона. В
линейные напряжения составляют V12, V23 и V32 с линейно-
нейтральные напряжения показаны как V1N, V2N и V3N.Фигура
3 показаны правильные линейные векторные напряжения для 3-х фазного преобразователя.
фаза 3-проводная конфигурация треугольника с выбранным вектором V12
в качестве ссылки. Примечание: любой вектор может быть выбран как
ссылка, выбор совершенно произвольный.
4-проводная 3-фазная система звезды
показан на рисунке 2 с V1N, выбранным в качестве эталона. В
линейные напряжения составляют V12, V23 и V32 с линейно-
нейтральные напряжения показаны как V1N, V2N и V3N.Фигура
3 показаны правильные линейные векторные напряжения для 3-х фазного преобразователя.
фаза 3-проводная конфигурация треугольника с выбранным вектором V12
в качестве ссылки. Примечание: любой вектор может быть выбран как
ссылка, выбор совершенно произвольный.
Последовательность фаз:
Последовательность фаз определяет последовательную синхронизацию, по которой
каждый вектор линейного напряжения отстает друг от друга линейное напряжение
вектор против часовой стрелки.Рисунки 1, 2 и
3 показана последовательность фаз {1-2-3}. Последовательность {1-2-3}
означает, что V12 опережает V23 на 120 градусов, а V23 опережает
V31 на 120 градусов. Кроме того, V1N опережает V2N на 120
градусов, а V2N опережает V3N на 120 градусов. это
необходимо установить последовательность фаз перед выполнением
любые вычисления для того, чтобы вычисленный вектор вектора
углы могут быть правильно расположены друг относительно друга.
Кроме того, V1N опережает V2N на 120
градусов, а V2N опережает V3N на 120 градусов. это
необходимо установить последовательность фаз перед выполнением
любые вычисления для того, чтобы вычисленный вектор вектора
углы могут быть правильно расположены друг относительно друга.
Есть только две допустимые последовательности фаз; {1-2-3}
последовательность и последовательность {3-2-1}. Обе эти фазы
последовательность определяется тем, как 3-фазный трансформатор
линии питания (L1, L2, L3) подключены и промаркированы.
На рисунке 4 показана последовательность {3-2-1} относительно
{1-2-3} последовательность. Примечание: последовательность фаз может быть
можно изменить, просто поменяв местами соединения любых двух
из трех (L1, L2, L3) линий питания; однако это
следует делать только в соответствии со всеми надлежащими
нормы, правила и одобрение заводского инжиниринга
штат сотрудников.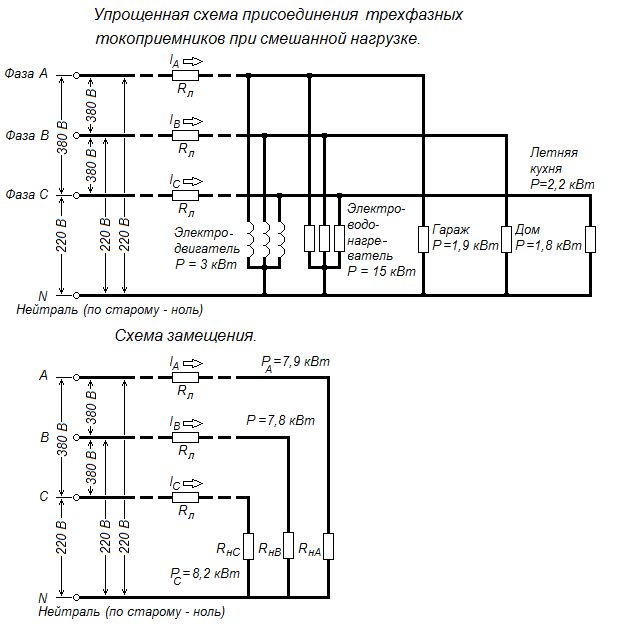
Индексы:
Соблюдение правильного порядка нижних индексов для всех векторов
количество — один из важнейших ключей к успеху
3-х фазные расчеты. На рисунке 4 показан правильный нижний индекс
порядок для каждой из двух различных фазовых последовательностей. За
последовательность {1-2-3}, правильный порядок индексов [12],
[23] и [31]; тогда как правильный порядок нижнего индекса для
последовательность {3-2-1} — это [32], [21] и [13].
Нижний индекс:
После определения последовательности фаз и правильного
индексы обозначены, расчеты по этим
индексов вместе с условными обозначениями, принятыми для
Версия закона Ома для переменного тока предотвратит угловые ошибки.
По соглашению, V12 — это падение напряжения вектора плюс (1) к
минус (2) в направлении тока, протекающего из точки
(1) к точке (2) и равен этому току, умноженному
импедансом переменного тока между точками (1) и (2). За
пример в векторной записи;
За
пример в векторной записи;
Сложение / вычитание векторов:
Правильная запись в нижнем индексе устанавливает правильный метод
для векторного сложения / вычитания векторов. На рисунке 2
фазоры линейного напряжения в этой трехфазной {1-2-3}
Последовательная 4-проводная система «звезда» состоит из линейно-нейтральной
векторные напряжения следующим образом;
Если среднеквадратичные напряжения между фазой и нейтралью равны (стандарт сбалансированной системы), то приведенные выше уравнения показывают, что все линейное напряжение питания фазора — фаза-нейтраль. напряжения, умноженные на 3, и подводят фазу к нейтрали векторы напряжения на 30 градусов .Например, стандартный 4-проводная 3-фазная система звезды с линейным напряжением 120 вольт и V1N, выбранный в качестве опорного вектора на ноль градусов имеет линейное напряжение;
V12 = 208∠ 30 °; V23 = 208∠ -90 °; V31 = 208∠ 150 °.
Важная концепция: Конфигурация трехфазного трехпроводного треугольника система уравновешивания напряжений фактически не имеет линейно- нейтральные напряжения, такие как звездочка.Тем не менее дельта-фазное напряжение, как показано на Рисунке 3, все еще может быть построенный из теоретического набора сбалансированных 3-фазных линейные напряжения, как показано выше. В отношения с этими теоретическими напряжениями чрезвычайно полезно для определения углов дельта-фазора.
Процедуры, инструкции и формулы расчетов
Следующий список процедур, рекомендаций и формул проиллюстрируйте схему расчета трехфазного фазора количества с использованием типовых данных на паспортной табличке, взятых из отдельные единицы нагрузки.Расчеты производятся следующим образом;
- Идентификация чередования фаз; {1-2-3} или {3-2-1}
- Определить индексы; [12], [23], [31] или [32], [21], [13]
- Предположим, что линейные токи L1, L2, L3 текут к нагрузкам.
 и нейтральный (обратный) ток течет к источнику питания.
и нейтральный (обратный) ток течет к источнику питания. - Ток нагрузки и падение напряжения должны соответствовать обозначения подстрочных индексов, как определено ранее.
- Используйте «Закон Ома для переменного тока» для расчета величин и углы каждой отдельной однофазной нагрузки Текущий. Просмотрите AN109 Dataforth, ссылка 1.
- Важные понятия: Линейные токи как для звезды, так и для
3-фазные нагрузки, сбалансированные по схеме треугольника, рассчитываются с использованием
следующие отношения;
- Входная мощность переменного тока = 3 x (Vline) x (Iline) x PF
- PF — косинус угла, на который прямая
токи опережают или отстают от линейного напряжения.Фактическое трехфазное напряжение фаза-нейтраль
существуют в конфигурациях звезды; тогда как они
теоретический в дельта-конфигурациях.
 Например,
принять любую сбалансированную 3-фазную нагрузку на 10 ампер
линейного тока и коэффициент мощности запаздывания 0,866 (30 °). Если
системная последовательность {1-2-3} и V12 является справочным,
тогда I1 = 10∠ -60 °; I2 = 10∠ 180 °; I3 = 10∠ 60 °.
Например,
принять любую сбалансированную 3-фазную нагрузку на 10 ампер
линейного тока и коэффициент мощности запаздывания 0,866 (30 °). Если
системная последовательность {1-2-3} и V12 является справочным,
тогда I1 = 10∠ -60 °; I2 = 10∠ 180 °; I3 = 10∠ 60 °.
- Определите количество треугольников мощности; Вт «P» и VARs «Q» для каждой нагрузки. Ссылка на обзор 1.
- Суммировать ранее рассчитанную индивидуальную нагрузку токи с использованием правильной записи индекса для определения каждая отдельная строка тока
- Наконец, просуммируйте все отдельные треугольники мощности нагрузки.
количества (Вт «P» и VAR «Q») для определения
количество треугольников мощности системы; P, Q и PF.Это
этот последний шаг, который определяет, как загружается система
население ведет себя.

Примеры расчетов
В следующих примерах предполагается типичное напряжение 208–120 вольт. трехфазная конфигурация 4 звезды с чередованием фаз из {1 2 3}, и V12 выбран в качестве ссылки. Это звёздочка система; однако нагрузки, подключенные между каждым из три отдельные линии питания (L1, L2, L3) составляют 208-вольтная 3-проводная конфигурация, треугольник.Три категории однофазные нагрузки принимаются для следующих расчеты. Эти категории идентичны тем определено в Руководстве по применению AN109 (Ссылка 1) и перечисленные ниже с необходимыми данными паспортной таблички.- Выходные киловатты; КВт, КПД (опция), PF = 1
- Выходная мощность в лошадиных силах; HP, КПД, P
- Входная кВА; КВА, ПФ, КПД 100%.
В таблице 1 приведены расчетные значения для предполагаемого население этих нагрузок.
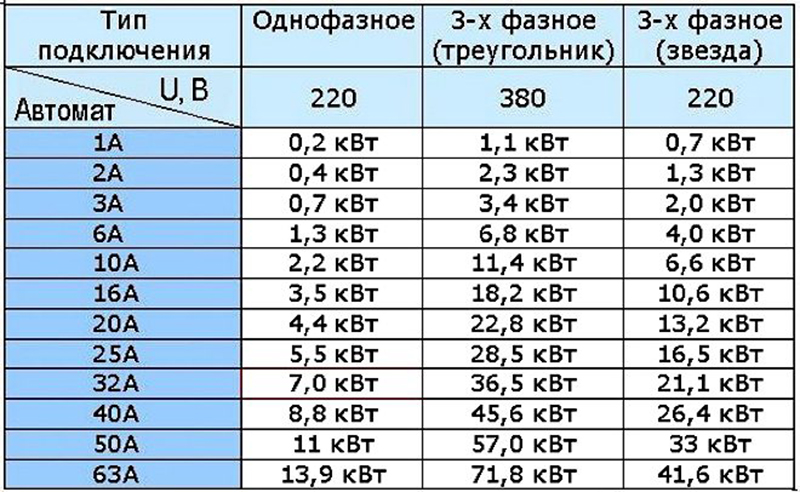 Читатели должны проверить эти
расчеты. Dataforth предлагает интерактивный Excel
рабочая тетрадь, аналогичная Таблице 1, которая автоматически
рассчитывает все величины трехфазной системы. Видеть
Ссылка 2 для загрузки загрузите этот файл Excel.
Читатели должны проверить эти
расчеты. Dataforth предлагает интерактивный Excel
рабочая тетрадь, аналогичная Таблице 1, которая автоматически
рассчитывает все величины трехфазной системы. Видеть
Ссылка 2 для загрузки загрузите этот файл Excel. Пример расчета для нагрузок между фазой и нейтралью
Трехфазные звездообразные системы с нейтралью могут иметь одинаковые или
неравные отдельные однофазные нагрузки, подключенные между
любой из линий питания (L1, L2, L3) и нейтраль.Системы
сбалансированы, если все нагрузки между нейтралью идентичны.
На рисунке 5 показаны три группы однофазных линейно-нейтральных нагрузки, подключенные по трехфазной системе «звезда». Эта конфигурация однофазных нагрузок может быть рассматривается как составная несбалансированная звездообразная нагрузка
На рисунке 6 показаны три группы однофазных межфазных
нагрузки, подключенные по трехфазной системе «звезда». Этот
конфигурацию однофазных нагрузок можно рассматривать как
композитная несбалансированная дельта-нагрузка
Этот
конфигурацию однофазных нагрузок можно рассматривать как
композитная несбалансированная дельта-нагрузка
На рисунке 7 показаны группа сбалансированных нагрузок звездой и группа сбалансированных дельта-нагрузок, обе из которых (могут быть) подключен по трехфазной системе звезды.
Таблица 1 представляет собой составной набор расчетных результатов для конфигурации, показанные на рисунках 5, 6 и 7.Эти расчеты предполагают произвольную популяцию типа загружает ранее определенные и использует все правила, процедуры и определения, как показано выше. В Результаты системы из расчетов Таблицы 1 показаны ниже. в таблицах 2 и 3.
Напряжение сети V12 (208 при нулевом градусе) является опорным для указанные выше текущие углы.
Читателям предлагается проверить эти расчеты.
Как упоминалось выше, Dataforth предоставляет интерактивный Файл Excel, предназначенный для помощи энтузиастам-исследователям. при расчете системных токов и сопутствующей мощности уровни. Этот файл позволяет исследователю ввести паспортную табличку. данные по всем системным нагрузкам; после чего ток всей линии векторов и мощности рассчитываются автоматически. «Интерактивная рабочая тетрадь Excel для трех- Расчет фаз переменного тока »можно загрузить с Веб-сайт Dataforth, см. Ссылку 2.
Рисунок 8 — иллюстрация изолированного истинного значения Dataforth.
Модуль ввода RMS, SCM5B33. Эта функция также
доступен в упаковке на DIN-рейку; DSCA33. Dataforth
имеет набор модулей преобразования сигналов, спроектированных
специально для измерения переменного среднеквадратичного значения высокого напряжения
параметры с использованием встроенного затухания. Читатель
рекомендуется посетить ссылки 1, 6, 7 и 8.Ссылки на Dataforth Читателю предлагается посетить веб-сайт Dataforth и
изучить их полную линейку изолированного преобразования сигнала
модули и соответствующие примечания по применению, см. ссылки
показано ниже.
Читатель
рекомендуется посетить ссылки 1, 6, 7 и 8.Ссылки на Dataforth Читателю предлагается посетить веб-сайт Dataforth и
изучить их полную линейку изолированного преобразования сигнала
модули и соответствующие примечания по применению, см. ссылки
показано ниже.
- Dataforth Corp., http://www.dataforth.com
- Dataforth Corp., AN110 Excel Интерактивная работа Книга для расчетов трехфазного переменного тока
- Dataforth Corp., Примечание по применению AN109, Измерения однофазного переменного тока
- Dataforth Corp., AN109 Excel Интерактивная работа Книга для расчетов однофазного переменного тока
- Национальный электротехнический кодекс контролируется Национальной пожарной службой Агентство по охране, NFPA
- Dataforth Corp.
 , Система аттенюатора напряжения SCMVAS,
, Система аттенюатора напряжения SCMVAS, - Dataforth Corp., серия модульных формирователей сигналов с истинным среднеквадратичным значением SCM5B33
- Dataforth Corp., серия DSCA33 формирователей сигналов True RMS для монтажа на DIN
Какова формула трехфазной цепи?
Введение
Трехфазная цепь состоит из трехфазного источника, трехфазной нагрузки и трехфазной линии передачи.Самая основная характеристика этой схемы — наличие одной или нескольких групп источников питания. Каждая группа состоит из трех источников питания синусоидальной формы с одинаковой амплитудой, одинаковой частотой, разностью фаз 120 °, а источник питания и нагрузка соединены определенным образом. Трехфазные цепи широко используются в энергосистемах, таких как производство, передача, распределение и электрическое оборудование большой мощности.
Что означает 3 фазы?
Каталог
Ⅰ Основы трехфазной схемы
Три фазы могут быть запитаны по шести проводам, причем два провода зарезервированы для исключительного использования каждой фазы.Однако они обычно поставляются только по трем проводам , а фазное или линейное напряжение — это напряжения между тремя возможными парами проводов. Фазные или линейные токи — это токи в каждом проводе. Напряжения и токи обычно выражаются как действующие или действующие значения, как в однофазном анализе.
1.1 Характеристика трехфазной цепи
Специальное питание
Специальная нагрузка
Специальное соединение
Специальное решение
1.2 Условия трехфазной цепи
1) Концевой провод (пожарный)
2) Нейтраль
3) Линейный ток
4) Линейное напряжение
5) Фазный ток
6) Фазное напряжение
7) Трехфазная трехпроводная система и трехфазная четырехпроводная система проводов
1.
 3 Трехфазное напряжение и ток
3 Трехфазное напряжение и ток Резюме: линейное напряжение в зависимости от фазового напряжения
1) Линейный ток равен соответствующему фазному току.
2) Если фазное напряжение симметрично, линейное напряжение также симметрично.
3) Напряжение сети в √3 раз больше фазного напряжения.
4) Фаза сетевого напряжения опережает соответствующее фазное напряжение на 30 ° .
Резюме: Линейный ток против фазного тока
1) Линейное напряжение равно соответствующему фазному напряжению.
2) Если фазные токи симметричны, линейные токи также симметричны.
3) Линейный ток в √3 в раз больше фазного напряжения.
4) Фаза сетевого тока отстает от соответствующего фазного напряжения на 30 ° .
1.4 Преимущества трехфазной цепи
Выработка электроэнергии: трехфазная мощность увеличивается на 50% по сравнению с однофазной мощностью.
Коробка передач: На 25% на меньше материала, чем при передаче по однофазной цепи. То есть при определенных условиях для передачи определенного количества мощности по трехфазной сети требуется только 75% меди для однофазной передачи.
Распределение энергии: более экономично, чем однофазные трансформаторы, и легче подключается к нагрузке.
Транспортировка: простая конструкция, низкая стоимость, надежная работа, удобство обслуживания.
Кроме того, три провода обычно используются в высоковольтных линиях электропередачи, будь то на опорах или столбах, со штыревыми или подвесными изоляторами. Некоторые высоковольтные линии теперь являются постоянным током, поскольку твердотельные устройства упрощают преобразование в переменный ток и обратно. В линиях постоянного тока отсутствуют проблемы, связанные с фазой, а также устранен скин-эффект, который уменьшает эффективную площадь проводников.Управлять передачей электроэнергии на большие расстояния не так просто, как может показаться.
Ⅱ Симметричный и асимметричный
2.1 Симметричная трехфазная цепь
Симметричный трехфазный источник питания обычно генерируется трехфазным синхронным генератором, как показано на рисунке (а). Среди них трехфазные обмотки различаются по пространству на 120 °. Когда ротор вращается с равномерной угловой скоростью ω, в трехфазной обмотке генерируется индуцированное напряжение, тем самым образуя симметричный трехфазный источник питания, как показано на рисунке (b).Среди них три конца A, B и C называются начальным концом, а три конца X, Y и Z называются концом. Когда вы подключаете нагрузку к трем проводам, это нужно делать так, чтобы это не нарушало симметрию.
Мгновенное напряжение Расчет трехфазной мощности
В формуле возьмем напряжение фазы A u A в качестве опорной величины синуса. Диаграмма формы трехфазного напряжения показана на рисунке (а).
Ключ к пониманию трехфазного тока — это понимание векторной диаграммы напряжений или токов. Вектор трехфазного источника питания можно представить на рисунке (б).
Характеристики симметричного трехфазного источника питания могут быть получены из приведенной выше формулы:
Из приведенной выше формулы сумма мгновенного значения трехфазного источника питания и сумма векторов всегда равны нулю.
Последовательность, в которой каждая фаза трехфазной мощности проходит через одно и то же значение (например, максимальное значение), называется последовательностью фаз трехфазной мощности, а последовательность фаз упомянутого выше трехфазного напряжения называется положительной последовательностью.И наоборот, если фаза B превышает 120 ° фазы A, а фаза C превышает 120 ° фазы B, эта последовательность фаз называется обратной последовательностью. Если нет специальных инструкций, обычно по умолчанию используется положительный порядок.
2.2 Трехфазная асимметрия
1) В трехфазной цепи, если имеется асимметричная часть, это называется трехфазной асимметрией.
2) Комплексная мощность, потребляемая трехфазной нагрузкой, равна сумме различных комплексных мощностей.
3) Мгновенная мощность трехфазной цепи — это сумма мгновенной мощности каждой фазной нагрузки.
4) В трехфазной трехпроводной схеме, симметричной или несимметричной, для измерения трехфазной мощности можно использовать два измерителя мощности.
Когда напряжение источника питания в трехфазной цепи асимметрично или параметры в цепи асимметричны, ток в цепи обычно асимметричен. Такая схема называется трехфазной асимметрией. В трехфазных цепях очень много деталей несимметрии, и причины разные. Например, в трехфазной цепи много маломощных однофазных нагрузок, их сложно объединить в полностью симметричную цепь.Когда трехфазная цепь разрывается или замыкается накоротко, это также трехфазная цепь асимметрии. Кроме того, в некотором электрическом оборудовании и инструментах формально для работы используется трехфазная асимметрия.
Например, самая распространенная низковольтная трехфазная четырехпроводная система. Из-за большого количества однофазных нагрузок в низковольтной системе эквивалентные импедансы Z A , Z B и Z C трехфазной цепи обычно отличаются друг от друга, а мощность напряжение питания в целом можно считать симметричным.Таким образом, симметричный трехфазный источник питания преобразуется в асимметричную трехфазную нагрузку.
Схема, показанная на рисунке, имеет два узла, и напряжение между двумя узлами может быть вычислено напрямую в соответствии с методом узлового напряжения.
Хотя напряжение источника питания в приведенной выше формуле является симметричным, напряжение между нейтральной точкой источника питания и нейтральной точкой нагрузки не равно нулю из-за асимметрии нагрузки, то есть U NN ≠ 0.Согласно закону Кирхгофа о напряжении , фазное напряжение нагрузки можно получить как:
Векторная диаграмма каждого напряжения, соответствующего приведенной выше формуле, выглядит следующим образом:
Ⅲ Формулы мощности в трехфазной цепи
1. Средняя мощность
Средняя мощность
Предположим, что мощность, потребляемая фазной нагрузкой в симметричной трехфазной цепи, равна P p = U p I p cosφ , где U p — фазное напряжение, а I p — фазный ток нагрузки.Тогда общая трехфазная мощность составляет: P = 3U p I p cosφ
Обратите внимание на
1) φ в приведенной выше формуле — это угол разности фаз (угол импеданса) фазного напряжения и фазы. Текущий.
2) cosφ — коэффициент мощности каждой фазы в симметричной трехфазной системе:
cosφA = cosφB = cosφC = cosφ
3) Формула рассчитывает мощность цепи (или мощность, потребляемую нагрузкой) .
Когда нагрузка подключена звездой, линейное напряжение и линейный ток на конце нагрузки подставляются в приведенную выше формулу:
Когда нагрузка подключена треугольником, линейное напряжение и линейный ток на конце нагрузки подставляются в приведенную выше формулу:
2. Реактивная мощность
Реактивная мощность
Реактивная мощность, потребляемая нагрузкой в симметричной трехфазной цепи, равна сумме реактивной мощности каждой фазы:
3. Полная мощность
4. Мгновенная мощность
Предположим, что напряжение и ток фазы A трехфазной нагрузки равны:
Тогда мгновенная мощность каждой фазы равна:
Можно доказать, что их сумма равна
Приведенная выше формула показывает, что мгновенная мощность симметричной трехфазной цепи постоянна и равна средней мощности.Это одно из преимуществ симметричной схемы. Например, в трехфазном двигателе достигается сбалансированный электромагнитный момент и устраняется механическая вибрация, чего нет в однофазных двигателях.
Ⅳ Часто задаваемые вопросы о трехфазной цепи1. Что такое трехфазная цепь?
Трехфазное питание — это трехпроводная силовая цепь переменного тока, в которой каждый фазный сигнал переменного тока разнесен на 120 электрических градусов. … трехфазный — это то, что трехфазный источник питания лучше выдерживает более высокие нагрузки. Однофазные источники питания чаще всего используются, когда типичными нагрузками являются освещение или обогрев, а не большие электродвигатели.
… трехфазный — это то, что трехфазный источник питания лучше выдерживает более высокие нагрузки. Однофазные источники питания чаще всего используются, когда типичными нагрузками являются освещение или обогрев, а не большие электродвигатели.
2. Сколько проводов в 3 фазе?
четыре провода
Трехфазная система состоит из четырех проводов. Три — проводники, а один — нейтральный.
3. Какова формула 3-фазной мощности?
Трехфазные расчеты.Для трехфазных систем мы используем следующее уравнение: кВт = (В × I × PF × 1,732) ÷ 1000.
4. В чем преимущество трехфазной системы?
Трехфазная цепь обеспечивает большую удельную мощность, чем однофазная, при той же силе тока, что позволяет уменьшить размер проводки и снизить затраты. Кроме того, трехфазное питание упрощает балансировку нагрузок, сводит к минимуму токи гармоник и необходимость в больших нейтральных проводах.
5.Что подразумевается под трехфазной сбалансированной нагрузкой?
Сбалансированное трехфазное напряжение или ток — это напряжение, в котором размер каждой фазы одинаков, а фазовые углы трех фаз отличаются друг от друга на 120 градусов. … При такой сбалансированной нагрузке, если применяется сбалансированное трехфазное питание, токи также будут сбалансированы.
Альтернативные модели
| Деталь | Сравнить | Производителей | Категория | Описание | |
| ПроизводительЧасть #: EP1S10F780C7 | Сравнить: EP1S10F780C5N VS EP1S10F780C7 | Производитель: Altera | Категория: ПЛИС | Описание: FPGA Stratix Family 10570 Cells 420. 17 МГц, 130 нм, 1,5 В, 780 контактов, FC-FBGA 17 МГц, 130 нм, 1,5 В, 780 контактов, FC-FBGA | |
| Номер детали: EP1S10F780C7N | Сравнить: Текущая часть | Производитель: Altera | Категория: ПЛИС | Описание: FPGA Stratix Family 10570 Cells 420.17 МГц, 130 нм, 1,5 В, 780 контактов, FC-FBGA | |
| Номер детали: EP1S10F780C5 | Сравнить: EP1S10F780C7N VS EP1S10F780C5 | Производитель: Altera | Категория: ПЛИС | Описание: FPGA Stratix® Family 10570 Cells 500MHz 130nm Technology 1. 5V 780Pin FC-FBGA 5V 780Pin FC-FBGA | |
| Номер детали: EP1S10F780C6 | Сравнить: EP1S10F780C7N VS EP1S10F780C6 | Производитель: Altera | Категория: ПЛИС | Описание: FPGA Stratix® Family 10570 Cells 450.05 МГц, 130 нм, 1,5 В, 780 контактов, FC-FBGA |
— обзор
7.
 2.3 Метод модуляции прямого матричного преобразователя
2.3 Метод модуляции прямого матричного преобразователяВ этом разделе будет описана матрица рабочего цикла для управления каждым переключателем трехфазного прямого матричного преобразователя и метод модуляции трехфазного прямого матричного преобразователя с использованием матрицы рабочего цикла. Входное фазное напряжение и выходной фазный ток прямого матричного преобразователя даны как независимые переменные в формуле. (7.12).
(7.12) vi = vsavsbvsc = Vimcosωitcosωit − 2π / 3cosωit + 2π / 3, io = ioAioBioC = Iomcosωot − ϕocosωot − ϕo − 2π / 3cosωot − ϕo + 2π / 3.
В этом случае предположим, что операция генерирует выходное фазное напряжение и входной фазный ток в формуле. (7.13) контролем.
(7,13) vo = voAvoBvoC = Vomcosωotcosωot − 2π / 3cosωot + 2π / 3, ii = isaisbisc = Iimcosωit − ϕicosωit − ϕi − 2π / 3cosωit − ϕi + 2π / 3,
где cos ( ϕ ) и cos ( ϕ i ) — коэффициенты мощности нагрузки и входного каскада, соответственно, а ω i и ω o — входная и выходная угловые частоты, соответственно. Опорный потенциал выходного фазного напряжения v oA , v oB и v oC является нейтральной точкой трехфазного источника напряжения входного каскада, как показано на рис. 7.3. .
Опорный потенциал выходного фазного напряжения v oA , v oB и v oC является нейтральной точкой трехфазного источника напряжения входного каскада, как показано на рис. 7.3. .
Входная мощность прямого матричного преобразователя должна быть равна выходной мощности. Следовательно, уравнение. (7.14) определяется из v i T i i = v o T i o .
(7.14) VimIimcosϕi = VomIomcosϕo.
Когда коэффициент усиления по напряжению прямого матричного преобразователя определяется как q = V om / V im , Eq. (7.15) определяется как
(7.15) Vom = qVim, Iim = qIomcosϕocosϕi.
Когда уравнения. (7.12), (7.13) подставляются в уравнение. (7.10) матрица T скважности, которая удовлетворяет ограниченному условию продолжительности включения, как в уравнении. (7.11) рассчитывается с использованием уравнения. (7.16).
(7.11) рассчитывается с использованием уравнения. (7.16).
(7.16) T = dAadAbdAcdBadBbdBcdCadCbdCc = p13d1d2d3d3d1d2d2d3d1 + p23d1′d2′d3′d2′d3′d1′d3′d1′d2 ′,
, где d d39 1 39 , d 1 ‘, d 2 ‘ и d 3 ‘выражаются в уравнении. (7.17).
(7.17) d1 = 1 + 2qcosω1t, d2 = 1 + 2qcosω1t + 2π3, d3 = 1 + 2qcosω1t − 2π3, d1 ′ = 1 + 2qcosω2t, d2 ′ = 1 + 2qcosω2t − 2π3, d3 ′ = 1 + 2qcosω2t + 2π3,
, где ω 1 и ω 2 составляют ω o — ω i и ω o + ω i , соответственно, и p 1 и p 2 являются переменными управления коэффициентом мощности положительного и отрицательного направления, соответственно, которые выражены в формуле.(7.18).
(7.18) p1 = 121 + p, p2 = 121 − p, p = tanϕitanϕo.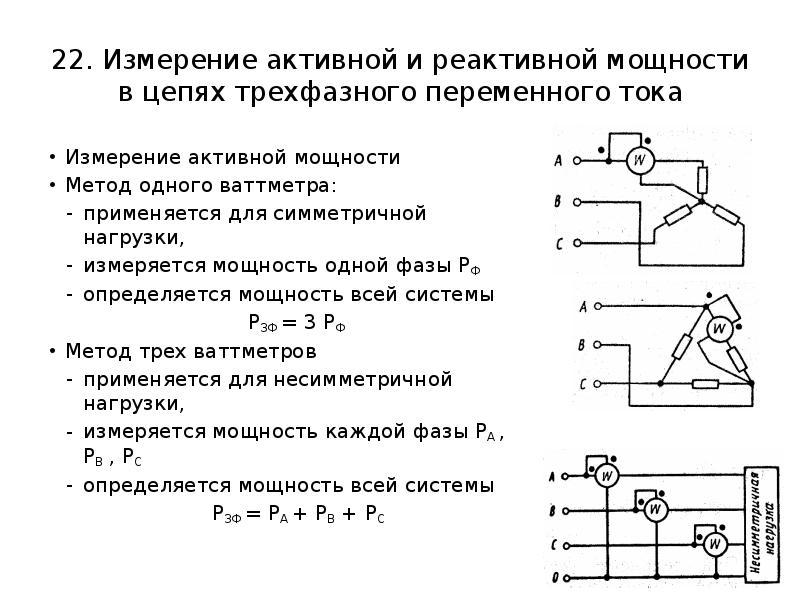
Из уравнения. (7.18), p 1 + p 2 = 1 и p 1 — p 2 = p . Кроме того, p — это коэффициент передачи фазы между входом и выходом прямого матричного преобразователя. Среди переменных, которые определяют p , ϕ o определяется характеристиками нагрузки, а ϕ i определяется желаемым значением команды.
Если входной каскад матричного преобразователя работает с единичным коэффициентом мощности ( ϕ i = 0), уравнение. (7.16) можно просто переписать, как это дает Ур. (7.19).
(7,19) djk = 131 + 2vojvskVim2j = ABCk = abc.
На рис. 7.10 показан диапазон значений трехфазного входного напряжения источника и выходного фазного напряжения прямого матричного преобразователя. Трехфазное выходное фазное напряжение не может выходить за пределы диапазона входного фазного напряжения, поскольку выходное фазное напряжение прямого матричного преобразователя синтезируется из входного напряжения. Следовательно, максимальная величина выходного фазного напряжения ограничена 50% от входного фазного напряжения. Другими словами, максимальное значение управляющего параметра q составляет 0,5 в матрице скважности уравнения. (7.16).
Следовательно, максимальная величина выходного фазного напряжения ограничена 50% от входного фазного напряжения. Другими словами, максимальное значение управляющего параметра q составляет 0,5 в матрице скважности уравнения. (7.16).
Рис. 7.10. Входное напряжение и выходное фазное напряжение ( q макс. = 0,5).
На рис. 7.11 показан способ получения большего выходного фазного напряжения, чем выходное фазное напряжение на рис. 7.10, путем добавления синфазного напряжения к выходному фазному напряжению по формуле.(7.13). Как упоминалось ранее, синфазное напряжение, приложенное к выходному фазному напряжению, не влияет на линейное напряжение выходного каскада прямого матричного преобразователя, поскольку опорные потенциалы выходного фазного напряжения v oA , v oB и v oC являются нейтральными точками трехфазного источника напряжения входного каскада.
Рис. 7.11. Входное напряжение и выходное фазное напряжение ( q макс. = 0.866) с использованием синфазного напряжения в модуляции.
= 0.866) с использованием синфазного напряжения в модуляции.
Следовательно, фазные напряжения на выходе выражаются в формуле. (7.20) как
(7.20) vo = voAvoBvoC = Vomcosωot + vcmtcosωot − 2π / 3 + vcmtcosωot + 2π / 3 + vcmt,
, где v cm — синфазное напряжение, выраженное в уравнении . (7.21) как
(7.21) vcmt = −16cos3ωot + 36cos3ωit.
В результате максимальное значение q увеличивается до √ 3/2 (= 0,866). Дополнительно q max = 0.866 — это уникальная характеристика прямого матричного преобразователя, которая определяется независимо от метода модуляции управления прямого матричного преобразователя.
Если выходное фазное напряжение уравнения. (7.20) вместо уравнения. (7.13) окончательное решение обычно выражается комплексным уравнением, полученным с помощью оптимального метода Вентурини. Кроме того, этот метод необходим для многих расчетов в реальном приложении. Однако, если входной каскад прямого матричного преобразователя работает с единичным коэффициентом мощности ( ϕ i = 0), окончательное решение может быть легко реализовано, как показано в уравнении.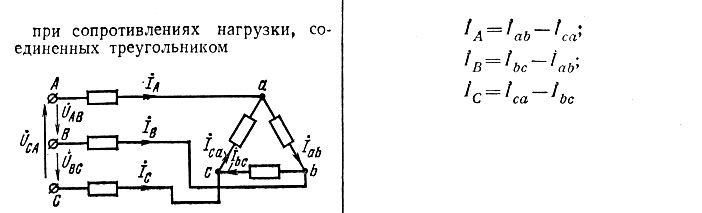 (7.22).
(7.22).
(7.22) djk = 131 + 2vojvskVim2 + 4q33sinωit + βksin3ωit, j = A, B, C, k = a, b, c, βa = 0, βb = −2π / 3, βc = 2π / 3.
В зависимости от оптимального анализа метода Вентурини, соотношение между передаточным отношением фазы на входе и выходе p прямого матричного преобразователя и коэффициентом усиления по напряжению q выбирается из уравнения. (7.23).
(7,23) 2qp⋅1 − signλ3 + sgnλ3≤1,
, где λ и sgn ( λ ) выражаются следующим образом в уравнении. (7.24).
(7.24) λ = 2q31 − p, signλ = 1, λ≥0−1, λ <0.
На рис. 7.12 показано изменение максимального усиления по напряжению q max в зависимости от значения p . Если p управляется для управления коэффициентом мощности входного каскада прямого матричного преобразователя, необходимо соблюдать осторожность, поскольку максимальное усиление напряжения q max изменяется, как показано на рис. 7.12.
7.12.
Рис. 7.12. Максимальное усиление напряжения q max в зависимости от значения p .
Если требуется, чтобы q max было> 0,5, диапазон p должен быть ограничен в диапазоне — 1 < p <1. Кроме того, в диапазоне - 1 < p <1, диапазон регулировки угла коэффициента мощности входного каскада ограничен как - | ϕ o | < ϕ i <| ϕ o | из уравнения. (7.18).
На рис. 7.13 показан пример метода, который генерирует стробирующие сигналы, которые являются функцией присутствия переключателя ( S jk ), с использованием каждого матричного элемента ( d jk ) матрицы заполнения . Т матричного преобразователя.Стробирующие сигналы переключателей S Aa , S Ab и S Ac , подключенных к выходному каскаду фазы A, определяются путем сравнения несущего сигнала v tri треугольной формы. форма с d Aa и ( d Aa + d Ab ) мгновенно. Кроме того, они выражаются следующим образом в формуле. (7.25):
форма с d Aa и ( d Aa + d Ab ) мгновенно. Кроме того, они выражаются следующим образом в формуле. (7.25):
Рис. 7.13. Формирование стробирующих сигналов из дежурного сигнала (переключение фазы А).
(7.25) sAasAbsAc = 100,0≤vtri , где s ij = 0 представляет состояние выключения переключателя и s ij = 1 представляет состояние включения. Методы, которые генерируют стробирующие сигналы переключателей ( S Ba , S Bb и S Bc ), подключенных к выходному каскаду B-фазы и переключателям ( S Ca , S Cb и S Cc ), подключенные к выходному каскаду C-фазы, аналогичны методу для переключателей, подключенных к выходному каскаду A-фазы. Дельта или сетчатое соединение ( Δ ) Система также известна как Трехфазная трехпроводная система ( 3-фазная 3-проводная ) и является наиболее предпочтительной системой для передачи электроэнергии переменного тока, а для распределения — звездой. обычно используется. В системе соединения Delta (также обозначаемой Δ ) начальные концы трех фаз или катушек соединены с конечными концами катушки. Или начальный конец первой катушки соединен с конечным концом второй катушки и так далее (для всех трех катушек), и это выглядит как замкнутая сетка или цепь, как показано на рис. (1). Проще говоря, все три катушки соединены последовательно, образуя тесную сеть или цепь. Из трех переходов вынуты три провода, и все токи, исходящие из перехода, считаются положительными. В соединении треугольником соединение трех обмоток выглядит как короткое замыкание, но это не так, , если система сбалансирована, тогда значение алгебраической суммы всех напряжений вокруг сетки равно нулю в соединении треугольником. Когда клемма разомкнута в Δ, то нет возможности протекать токи с базовой частотой вокруг замкнутой ячейки. Также читают: На заметку: В конфигурации «Дельта» в любой момент значение ЭДС одной фазы равно результату ЭДС двух других фаз, но в противоположном направлении. Теперь мы найдем значения линейного тока, линейного напряжения, фазного тока, фазных напряжений и мощности в трехфазной системе переменного тока треугольником. На рис.2 видно, что между двумя выводами имеется только одна фазная обмотка (т.е.е. между двумя проводами имеется одна фазная обмотка). Следовательно, в соединении Delta, напряжение между (любой парой) двух линий равно фазному напряжению фазной обмотки , которая подключена между двумя линиями. Поскольку последовательность фаз R → Y → B, следовательно, направление напряжения от фазы R к фазе Y положительное (+), а напряжение фазы R опережает напряжение фазы Y на 120 °. Аналогично, напряжение фазы Y опережает фазное напряжение B на 120 °, а его направление положительно от Y к B. Если линейное напряжение между; Тогда мы видим, что V RY опережает V YB на 120 °, а V YB опережает V BR на 120 ° . Допустим, В RY = В YB = В BR = В L …………… (Напряжение сети) Затем V L = V PH И.е. при соединении треугольником, линейное напряжение равно фазному напряжению . Из нижеприведенного (рис. 2) следует отметить, что полный ток каждой линии равен разности векторов между двумя фазными токами в соединении треугольником , протекающем по этой линии. т.е. {Vector Difference} Ток линии 1 можно найти, определив разность векторов между I R и I B , и мы можем сделать это, увеличив I B. Вектор в обратном порядке, так что I R и I B образуют параллелограмм. Диагональ этого параллелограмма показывает разность векторов I R и I B , которая равна току в строке 1 = I 1 .Более того, изменяя вектор I B на противоположное, он может указывать как (-I B ), следовательно, угол между I R и -I B (I B , при обратном изменении = -I B ) составляет 60 °. Если, I R = I Y = I B = I PH …. Фазные токи Тогда; Текущий по Линии 1 ток будет; I L или I 1 = 2 x I PH x Cos (60 ° / 2) = 2 x I PH x Cos 30 ° = 2 x I PH x (√3 / 2) …… Так как Cos 30 ° = √3 / 2 I L = √3 I PH и.е. При соединении по схеме треугольник линейный ток в √3 раза больше фазного тока. Точно так же мы можем найти два расширяющих линейных тока, как указано выше. т.е. I 2 = I Y — I R … Векторная разность = √3 I PH I 3 = I B — I Y … Разность векторов = √3 I PH As, все линейные токи равны по величине, т.е. I 1 = I 2 = I 3 = I L Отсюда IL = √3 I PH Это видно на рисунке выше; Связанное сообщение: Осветительные нагрузки, соединенные звездой и треугольником Мы знаем, что мощность каждой фазы; Мощность / фаза = В PH x I PH x CosФ А суммарная мощность трех фаз; Общая мощность = P = 3 x V PH x I PH x CosФ … ..(1) Мы знаем, что значения фазного тока и фазного напряжения при соединении треугольником; I PH = I L / √3… .. (Начиная с I L = √3 I PH ) V PH = V L Ввод этих значений в уравнение мощности ……. (1) P = 3 x V L x (I L / √3) x CosФ …… (I PH = I L / / √3) P = √3 x√3 x V L x (I L / √3) x CosФ… {3 = √3x√3} P = √3 x V L x I L x CosФ … Следовательно доказано; Питание в соединении треугольником , P = 3 x V PH x I PH x CosФ ….или P = √3 x V L x I L x CosФ Где Cos Φ = коэффициент мощности = фазовый угол между фазным напряжением и фазным током (не между линейным током и линейным напряжением). То же самое объясняется в MCQ трехфазной цепи с пояснительным ответом (MCQ № 1) Полезно помнить: При подключении по схеме «звезда» и «треугольник» общая мощность при сбалансированной нагрузке равна . Т.е. Общая мощность в трехфазной системе = P = √3 x V L x I L x CosФ Полезно знать: Сбалансированная система — это система, в которой: Также читают: % PDF-1.6
%
106 0 объект
>
эндобдж
165 0 объект
>
эндобдж
104 0 объект
> поток
Акробат Дистиллятор 5.0.5 (Windows) 2004-07-07T15: 23: 25Z2013-08-22T07: 29: 22-05: 002013-08-22T07: 29: 22-05: 00PScript5.dll, версия 5.2application / pdf 3-фазное питание, значения напряжения и тока
Трехфазное соединение треугольником: линия, фазный ток, напряжение и мощность в Δ конфигурации
Что такое соединение треугольником (Δ)? C: \ files \ курсы \ 3414 \ ece3414notes1a.wpd


 Учитывая немалые расстояния (сотни и тысячи километров) и то, что для проводов используют цветные металлы с малым удельным электрическим сопротивлением, экономия получается весьма существенной.
Учитывая немалые расстояния (сотни и тысячи километров) и то, что для проводов используют цветные металлы с малым удельным электрическим сопротивлением, экономия получается весьма существенной. Замечательное свойство таких двигателей – это возможность менять направление вращения ротора на обратное простым переключением двух любых фазных проводов.
Замечательное свойство таких двигателей – это возможность менять направление вращения ротора на обратное простым переключением двух любых фазных проводов.



 и нейтральный (обратный) ток течет к источнику питания.
и нейтральный (обратный) ток течет к источнику питания.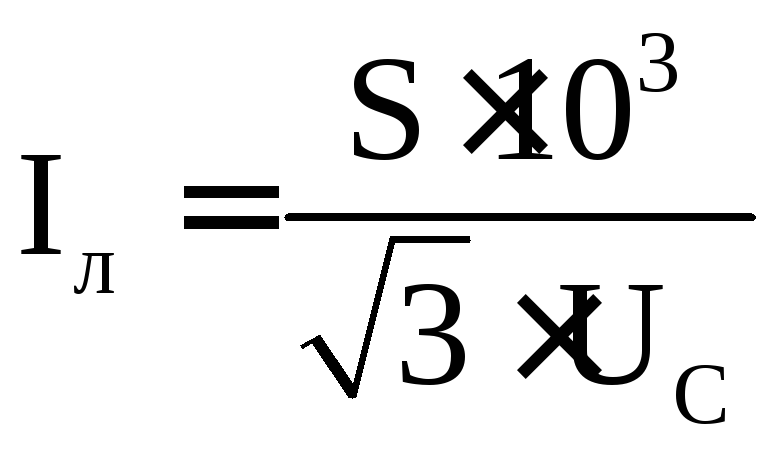 Например,
принять любую сбалансированную 3-фазную нагрузку на 10 ампер
линейного тока и коэффициент мощности запаздывания 0,866 (30 °). Если
системная последовательность {1-2-3} и V12 является справочным,
тогда I1 = 10∠ -60 °; I2 = 10∠ 180 °; I3 = 10∠ 60 °.
Например,
принять любую сбалансированную 3-фазную нагрузку на 10 ампер
линейного тока и коэффициент мощности запаздывания 0,866 (30 °). Если
системная последовательность {1-2-3} и V12 является справочным,
тогда I1 = 10∠ -60 °; I2 = 10∠ 180 °; I3 = 10∠ 60 °.
 , Система аттенюатора напряжения SCMVAS,
, Система аттенюатора напряжения SCMVAS,