Аргументы против покупки

● Это неоправданные расходы
Действительно, посудомойка стоит недешево, при этом расходы ждут владельцев и после покупки. Вместо обычного средства для мытья посуды придется покупать различные уходовые препараты.

Однако владельцы ПММ уверяют, что расходники стоят не так уж и дорого, а затраты на покупку компенсируются экономией времени и, как ни странно, воды. Экспериментально доказано, что при мытье посуды вручную воды можно использовать даже больше.

Что касается дополнительных трат на электроэнергию, они не так велики, если, конечно, не включать агрегат для каждой грязной тарелки, а дожидаться полной загрузки.

● ПММ занимает много места, ее придется встраивать
Действительно, такая техника довольно объемна и требует определенной площади для установки. Если размер кухни не превышает 5-6 м2, это действительно становится проблемой. Кроме того, место необходимо выбирать таким образом, чтобы машину можно было подключить к водоподводящим трубам, канализации, электросети.

Для тесной кухни можно найти компактный вариант, однако и вместительность у него будет соответствующая: такая техника подойдет для семьи численностью не более 3-4 человек.

Некоторые производители предлагают модели, совмещенные с другой техникой, такой вариант «3 в 1» или «2 в 1». Например, есть посудомойки, совмещенные с варочной панелью или духовым шкафом.

● Не всякую посуду можно мыть в ПММ
Действительно, предметы из дерева, алюминия, меди, тонкого стекла и хрусталя лучше в посудомойку не ставить. Не стоит также рисковать и мыть там посуду с ручной росписью, неглазурованную керамику. Однако если в семье не используют эти виды изделий для сервировки и готовки, то причин отказываться от ПММ нет.

● Не имеет смысла покупать ПММ, если в доме мало посуды
Действительно, большинство агрегатов довольно объемны и для полной загрузки придется копить посуду чуть ли не целый день. Такой подход совершенно не подходит минималистам, привыкшим обходиться одной кастрюлей и парой тарелок.

С другой стороны, такие люди могут найти совсем небольшие, настольные модели, которые рассчитаны на мытье одного-двух комплектов посуды.

● ПММ плохо отмывает загрязнения
Многие владельцы жалуются, что в машине плохо отмываются жирные сковороды, да и остатки пищи лучше удалять с посуды перед загрузкой. Все это так, однако качество мытья зависит от класса агрегата. Если уж решили приобрести такую технику, не стоит останавливать выбор на самой бюджетной модели.

● Помыть посуду руками быстрее
Да, цикл работы ПММ довольно длительный. Если семья небольшая, помыть несколько тарелок и чашек вручную можно гораздо быстрее.

С другой стороны, техника ведь работает сама, не требуя вашего участия — почему бы не расслабиться и не заняться в это время чем-то более приятным.

● Посудомойка требует ухода
Действительно, как и любая другая техника, ПММ требует некоторого внимания: пару раз в месяц рекомендуется мыть фильтры и разбрызгиватели, а также регулярно заправлять в машинку моющие средства — не так уж сложно, правда?

Почему ПММ — это здорово?

● Экономия времени
Пожалуй, это главный аргумент, который приводят сторонники покупки. На самом деле, количество сэкономленных минут прямо пропорционально количеству грязной посуды, которое необходимо вымыть в течение дня, и уровню дисциплинированности хозяев.

Если в доме живут взрослые люди, которые привыкли мыть за собой посуду сразу после использования, никакой экономии времени от покупки посудомойки они не заметят. А вот мама трех-четырех ребятишек, несомненно, почувствует немалое облегчение, если в доме появится такая помощница.

● Отличное качество мытья и дезинфекция
Если вы купили модель с несколькими режимами, в том числе с замачиванием и ополаскиванием, на качество мытья вам жаловаться не придется. Наоборот, посуда в ПММ отмывается при температуре около 100 градусов — ни одни руки не выдержат такого, а значит, в процессе обработки в машине она еще и дезинфицируется.

● Не нуждается в горячей воде
Как и стиральная машина, агрегат сам нагревает воду, то есть проблем с его использованием не будет даже в период отключения централизованного горячего водоснабжения.

● Чистота мойки и столешниц
При использовании ПММ гораздо проще сохранять в чистоте мойку, рабочую поверхность стола и фасады прилегающей к мойке мебели. При мытье посуды вода, мыльный раствор и частички загрязнений не разлетаются по кухне, поэтому времени на наведение порядка уйдет меньше.

● Посуда служит дольше
В процессе мытья поверхность посуды не страдает от воздействия абразивных материалов, нет риска случайно выронить намыленную тарелку или чашку из рук и разбить.

Кроме того, посудомойка имеет встроенную защиту от протечек, работает тихо, а функция отложенного старта позволяет мыть посуду ночью или в ваше отсутствие.

Таким образом, посудомоечная машина чаще всего необходима
● семье с большим количеством детей, особенно маленьких;
● пожилым одиноким людям, которым сложно выполнять даже обычные домашние дела;
● тем, кто ненавидит мыть посуду руками.

Но есть люди, которые вполне могут обойтись без такой техники, даже если могут себе ее позволить:
● аккуратные взрослые одиночки и семейные пары, привыкшие сразу убирать посуду за собой;
● те, кто слишком занят, чтобы часто готовить и есть дома;
● те, кто воспринимает мытье тарелок как определенный тип медитации (такие люди встречаются, хотя и редко).

В любом случае, решение о покупке стоит принимать, исходя из реалий вашей жизни, а не ориентироваться на популярность техники.

Факультет прикладной математики и механики

Дорогие абитуриенты факультета прикладной математики и механики!

Вы уже вошли в историю как первые поступающие на ФПММ во времена коронавируса!

Вы на себе ощутили, в какое нестабильное время мы живем!

Во всем мире происходит сокращение рабочих мест, растет конкуренция, теряется опора в жизни в виде стабильных и понятных профессий, появляются новые виды деятельности! Нефть теряет цену, автомобили Тесла уже в городе, во многих профессиях роботы и искусственный интеллект заменяют людей!

А вам предстоит сделать очень непростой выбор своего будущего. Вам необходимо рискнуть, сделать сегодня ставку на 6 лет вперед! Как же в этой ситуации не промахнуться?

Оглянитесь на прошлый опыт — всегда получалось так, что те, кто выбирал фундаментальную подготовку, лучше справлялись с любой непредвиденной ситуацией!

Мы предлагаем вам именно это — получить классное фундаментальное образование, ощутить твердую опору под ногами, фундамент, которому не страшен никакой экономический кризис!

Из чего складывается фундаментальная подготовка? — Из физики, математики, механики, информационных технологий! И всему этому учат у нас!

Сейчас во всем мире переходят на использование цифровых двойников при проектировании, создании и эксплуатации объектов: в строительстве — от жилых зданий до атомных станций, в инженерной работе — от кроссовок и велосипедов до автомобилей и самолетов, в науках о человеке — от отдельных зубов до взаимодействия всех систем человека в целом!

Это то, что ждет всех нас и очень скоро!

Что же для этого будущего вы сможете найти на ФПММ?

Профиль “Вычислительная механика и компьютерный инжиниринг” (ВМ, направление “Прикладная механика”) — создание и применение компьютерных моделей сложных инженерных систем! Компьютерное моделирование бионического дизайна и аддитивных технологий! Но для компьютерных моделей или цифровых двойников нужны математические модели! А, значит, — математика, физика, механика, химия.

Профиль “Математическое моделирование” (ММ, направление “Прикладная математика и информатика”) — разработка математических моделей, как новых материалов, так и процессов их создания, математических моделей сложных систем от деформируемых конструкций из металлов, магнитомягких полимеров, астрофизических систем до иммунитета человека в его борьбе с вирусами!

Профиль “Динамика и прочность машин” (ДПМ, направление “Прикладная механика”) — анализ пригодности математических моделей материалов, проведение экспериментов, исследование и предсказание прочности и долговечности материалов и конструкций, деталей двигателя самолета, оптоволоконных датчиков под действием агрессивных сред, температур, лазеров! ДПМ-щиков ждут на всех промышленных предприятиях нашей страны!

“Фотоника и оптоинформатика” — направление, которое пронизывает все новые технологические сферы — передача информации, квантовые вычисления, оптоволоконные датчики, системы управления, интегральные оптические схемы! Датчики нужны везде — в атомных реакторах, в скважинах на огромной глубине, в двигателе самолета или автомобиля, на опасных химических производствах! Спрос на специалистов с такими знаниями постоянно растет! И мы готовим таких специалистов!

Датчики постоянно передают чудовищные объемы информации, их надо обрабатывать, принимать быстрые решения. Но компьютерное моделирование не всегда успевает! Что делать? — нужны системы искусственного интеллекта! А этим занимаются на ФПММ?

Да, есть целая научная школа, опытный коллектив! Где же этому можно научиться? На направлении “Информационные системы и технологии”!

На наших глазах происходит распространение беспилотного транспорта, как мирного, даже бытового, так и военного. Нужны новые решения, нужно опередить в научно-технологическом соревновании Китай и США. Где этому можно научиться? — На таком нашем направлении, как “Системы управления движением и навигация”! Здесь нужно и программировать на уровне железа, и собирать сложные электрические схемы, и применять математические методы, и разбираться в физике и механике!

Математическим методам в экономике тоже учат на ФПММ! Профиль “Математическое и информационное обеспечение экономической деятельности” (МИЭ, направление “Прикладная математика и информатика”) — разработка математических моделей для прогнозирования последствий принимаемых решений, использование информационных технологий для управления экономическими процессами предприятия и региона.

Наука о человеке тоже находит свое отражение на ФПММ в виде Биомеханики — это создание математических моделей систем человеческого организма, предсказание развития различных заболеваний и патологий, проектирование последствий хирургического вмешательств в организм! Но здесь вас ждет только магистратура! Для поступления на “Биомеханику” вам нужно будет 4 года учиться в баклавриате на любом из наших направлений!

Теперь вы знаете — ФПММ устремлен в будущее, ориентирован на высокие технологии!

У вас есть шанс учиться у лучших — учиться на ФПММ!

Делайте правильную ставку на свое будущее, поступайте правильно — поступайте на ФПММ!

Хочешь добиться успеха в жизни — научись решать трудные задачи! Самые трудные задачи учат решать на ФПММ!

Мы не оказываем образовательных услуг, мы создаем будущее — готовим ученых, инженеров, IT-специалистов!

До встречи на 1 курсе!

Декан ФПММ Иван Юрьевич Зубко

Пена в посудомоечной машине после мойки — причины, что делать

Бытовая техника создана для того, чтобы упрощать жизнь. Посудомоечная машина — не исключение. Она экономит силы и время, существенно облегчает быт. К тому же посуда, вымытая специальной техникой, намного чище, чем при ручном мытье приборов, тарелок, чашек, кастрюль.

Во время использования посудомоечной машины можно заметить, что после мытья посуды остается много пены. Это может указывать на неправильную эксплуатацию техники или ее неисправность. Если проблема несерьезная, вернуть ПММ в строй получится и самостоятельно. Но для начала нужно определить причину, почему в посудомоечной машинке остается пена.

Почему повышается пенообразование: распространенные причины

Если в новой посудомоечной машинке периодически или постоянно остается пена на дне после окончания цикла, нужно отключить прибор от сети и перекрыть подачу воды. Чтобы предотвратить вытекание воды на пол, нужно сразу заняться ее удалением из прибора. И только потом можно начинать выяснять, почему случилась такая неполадка или обращаться в ремонт посудомоечных машин.

Вот основные причины появления пены в посудомоечной машине после мойки:

• плохое качество моющего препарата. Хороший «расходник» обеспечивает бесперебойное функционирование техники. Можно выбрать такие формы выпуска, как таблетки, капсулы, моющий порошок или гель. При покупке препарата нужно обратить внимание на его стоимость, качество, дату выпуска;
• неверно подобранная дозировка. Если средство выбрано правильно, но из посудомоечной машины течет пена, это может быть признаком неправильной дозировки. Порошок нужно засыпать сухой мерной ложкой, иначе будут образовываться небольшие комки. Они оседают на дно, а при запуске нового цикла усиливают пенообразование ;
• неправильно настроенный цикл. Если выбрана не та программа, таблетка может не успеть растаять за отведенное время, в результате она оказывается на дне и включается в работу при следующем запуске мойки — появляется много пены. Чтобы таблетка полностью растворялась, нужно использовать режим, при котором вода нагревается до 50 градусов и выше;
• неправильный выбор средства. Если в посудомоечной машине стоит пена, это могло случиться из-за применения простого геля для ручного мытья посуды, а не специального препарата. Посудомоечная машинка не может правильно работать с такими средствами;
• остатки еды. В ПММ нельзя мыть посуду с большими кусками еды, иначе пена будет появляться даже без моющего средства. Некоторые продукты, например, сметана, яичный белок, некоторые виды теста, способны вступать в реакцию с моющим порошком и водой, из-за чего будет оставаться пена после цикла. Чтобы предотвратить это, нужно очищать тарелки или кастрюли от любой еды.

Если самостоятельно не получается установить, по какой причине идет пена из посудомоечной машины, стоит обратиться к мастеру, который проведет диагностику и отремонтирует технику.

Как исправить засор

Частая причина того, что остается пена после работы прибора, — засор на сетке мусорного фильтра. Такое случается при постоянной загрузке ПММ мисками и кастрюлями, покрытыми застывшим жиром. Он забивает отверстия, расположенные на дне камеры, из-за чего вода постепенно начинает уходить все хуже. В результате даже по окончании цикла в посудомоечной машинке можно увидеть остатки таблеток или геля.

Что нужно делать, если в посудомоечной машинке остается пена по причине возможного засора? Важно каждые пару недель прочищать фильтр — это предотвратит появление подобных проблем. Но если засор уже обнаружен, нужно сделать следующее:

1. Открыть дверцу камеры.
2. Извлечь корзину, размещенную внизу.
3. Выкрутить фильтр из поддона, достать металлическую сеточку.
4. Промыть все детали фильтрующего узла водой.
5. Установить элементы на место.

Пена в посудомоечной машине после мойки больше не будет появляться при условии регулярной прочистки фильтра.

Как очистить посудомоечную машину

Если пошла пена из ПММ, нужно строго следовать рекомендациям специалистов. Поэтапная инструкция, как избавиться от пены при поломке или неправильном применении посудомоечной машины :

1. Отключить устройство от сети. Достать посуду из камеры и удалить пену, вычерпывая ее ковшом в тазик.
2. При наличии моющего пылесоса можно удалить остатки с его помощью.
3. Вытереть дно камеры губкой.
4. Удалить остатки влаги сухой тряпкой. Работать нужно осторожно, чтобы не обжечься о нагревающиеся элементы.

Если в камере осталась пена, после выполнения вышеуказанных рекомендаций, важно использовать средство для поглощения пенной среды. Это может быть соль с уксусом или растительное масло. Нужно налить половину стакана уксуса на дно камеры и присыпать двумя горстями соли или использовать полстакана масла. Запустить ПММ. Процедуру можно повторить до полного очищения прибора.

Если принятые меры не помогли, пена все равно остается или устройство прекратило работать, нужно обратиться в ремонт посудомоечных машин. Такие неполадки сможет устранить только специалист. Опытные сотрудники компании «Топ Рефит» быстро установят причину поломки, проведут ремонт на дому, предоставят гарантию на свою работу. В сервисном центре есть возможность заказа срочного выезда мастера.

Проволока медная прямоугольная ПММ, ПМТ (М1), Cu-ETP

Есть ли у вас средства для дезинфекции посуды в посудомоечных машинах (ПММ)?

15.06.2020

В последнее время появились запросы на поставку дезинфицирующих средств (ДС) для ПММ.  Связано это с Письмом Роспотребнадзора  от 30 мая 2020 года «Рекомендации по организации работы предприятий общественного питания в условиях сохранения рисков распространения COVID-19». Чтобы сэкономить Вам время отвечаем сразу – доступное решение есть, «волшебного” средства нет. Теперь подробно почему.

1. Обратите внимание, что это РЕКОМЕНДАЦИИ, а не требования.
2. Если ПММ у Вас работает нормально – температура обработки посуды при ополаскивании составляет примерно 85°С, что само по себе обладаем дезинфицирующим эффектом. Но не даёт 100% гарантии удаления всей вредной микрофлоры.
3. Каждое ДС имеет рекомендованное время экспозиции в среднем 15 минут (в зависимости от концентрации рабочего раствора). В то же время, цикл полной мойки в профессиональной ПММ составляет в зависимости от режима 3 минуты. Вывод –дезинфицировать посуду в ПММ невозможно.
4. Существуют специализированные ПММ, которые могут применяться для дезинфекции посуды. Но стоят они дорого, цикл обработки достаточно продолжителен и использование их в предприятиях общепита в целом нецелесообразно.

Что же тогда делать? Всё просто – работайте в соответствии с существующими правилами и нормами учитывающие сложившуюся эпидемиологическую обстановку. Компания Долфин рекомендует следующее решение:

1. Предварительное замачивание посуды в растворе средства Prime. Задача – убрать остатки пищи.
2. Мойка посуды в ПММ средствами Regular и Dry если у вас вода мягкая или средней жёсткости, или Hard и Acid Dry, если у Вас вода жёсткая.
3. Замачивание посуды в 5% дезинфицирующем растворе K 001 Петролайт на время пандемии COVID-19 или 0,4% в обычное время.
4. Помните, для ополаскивания обработанной посуды необходимо использовать «чистые» продезинфицированные кассеты или решётки. Так же при работе с продезинфицированной посудой необходимо менять перчатки или обработать руки антисептиком К 002 Septo-Max.
5. При желании Вы можете добиться дополнительного дезинфицирующего эффекта используя для ополаскивания посуды в ПММ средство Promnova Acid LF M2. В качестве действующего вещества здесь используется смесь перекиси водорода и надуксусной кислоты, они не оставляют на поверхности разводов и опасных веществ (сами разлагаются на безопасные компоненты или испаряются с неё), эффективны уже в концентрации сотых долей процента, хорошо зарекомендовали себя на пищевых производствах. Однако надо помнить что средства, содержащие эти действующие вещества, требуют строгого выполнения мер безопасности: обязательно использовать СИЗ, так как оставляют сильные ожоги если неправильно обращаться с концентратом; имеют запах, поэтому надо следить что бы канистры были закрыты, хранились в помещении с хорошей вентиляцией и желательно при температуре до 20⁰С.

Наши инженеры готовы провести аудит Вашей ПММ и если это возможно — перенастроить ее на новый режим.

Обращайтесь за консультациями в компанию Долфин по бесплатному телефону 8 800 5508038

Скрытая марковская модель — обзор

3.2.2 Скрытые марковские модели

HMM — это популярный метод анализа траекторий сигнала во времени, полученных в результате биофизических экспериментов (Andrec, Levy, & Talaga, 2003; Bronson et al., 2009; Chung , Moore, Xia, Premkumar, & Gage, 1990; McKinney, Joo, & Ha, 2006; Qin, Auerbach, & Sachs, 2000; van de Meent et al. , 2014) — подробные описания можно найти в других источниках (Bishop, 2006). ; Colquhoun & Hawkes, 1995). Вкратце, в HMM предполагается, что усредненный по времени сигнал, зарегистрированный в течение каждого периода измерения, τ , на траектории сигнала, представляет некоторое «скрытое» состояние (т.е., траектория состояния). Затем предполагается, что лежащая в основе скрытая траектория состояния, которая не наблюдается напрямую, ведет себя как марковский процесс, управляемый в соответствии с вероятностями перехода. Как обсуждалось ранее, вероятности перехода одиночной молекулы в марковской системе связаны со стохастическими константами скорости, управляющими биомолекулярной системой. С помощью HMM вероятность того, что сигнал исходит из определенного скрытого состояния, рассчитывается с учетом скрытого состояния предыдущего периода времени, чтобы явно учесть вероятность перехода.Примечательно, что в HMM обычно предполагается, что значения сигнала, которые наблюдаются, когда одна молекула находится в определенном скрытом состоянии, распределяются в соответствии с нормальным распределением PDF (т. Е. Наблюдаемые сигналы будут моделью смеси Гаусса). Используя этот подход, можно «оценить» HMM, который описывает сигнал в терминах дискретного числа состояний и предоставляет в качестве параметров вероятности излучения сигнала для каждого состояния, а также вероятности перехода в виде матрицы вероятности перехода . P , из каждого штата.

При оптимальной оценке HMM, описывающей траекторию сигнала, можно использовать два разных метода для расчета стохастических констант скорости. В первом методе идеализированная траектория состояния может быть получена из HMM, а затем количественно определена, как описано, для использования с подходами распределения времени пребывания или анализа расширения вероятности перехода. Эта идеализированная траектория состояния получается путем применения алгоритма Витерби к HMM для создания пути Витерби (Viterbi, 1967).Путь Витерби, который напрямую дает траекторию идеализированного состояния, является наиболее вероятной последовательностью скрытых состояний, которые не только давали бы наблюдаемые значения сигнала при оптимальных вероятностях излучения сигнала, но и, скорее всего, возникали бы из оптимальных вероятностей перехода. Таким образом, важно отметить, что при использовании HMM для идеализации траектории сигнала результирующая идеализированная траектория состояния, а также вероятности испускания и перехода должны быть как можно более марковскими.Следовательно, если в исследуемой биомолекулярной системе присутствует какое-либо немарковское поведение, оно будет замаскировано и будет выглядеть как марковское. Чтобы избежать этого недостатка HMM, идеализированная траектория состояния может быть сгенерирована с использованием другого подхода, такого как определение порога.

Второй метод расчета стохастических констант скорости на основе оптимальной оценки НММ предполагает непосредственное использование вероятностей перехода, полученных на основе НММ. Хотя на первый взгляд кажется, что этот метод обходит использование идеализированных траекторий состояний, процесс оценки оптимального МММ, описывающего данные, по своей сути включает оценку скрытых состояний, сгенерировавших траекторию сигнала, и, следовательно, включает использование идеализированных траекторий состояний. траектории.Из HMM отдельные стохастические константы скорости могут быть рассчитаны с использованием уравнения. (8) и матрица вероятности перехода, аналогичная матрице, рассчитанной по идеализированной траектории состояния. Этот подход эквивалентен анализу разложения вероятности перехода. Как и при вычислении стохастических констант скорости по пути Витерби, следует отметить, что этот второй метод НММ также обеспечивает марковское поведение.

Наконец, отметим, что только в литературе по smFRET имеется несколько программных пакетов для анализа траекторий E _FRET на основе HMM.Из этих пакетов существует два типа подходов к оценке оптимального HMM, описывающего данные: подходы максимального правдоподобия (например, QuB (Qin, Auerbach, & Sachs, 1997), HaMMy (McKinney et al., 2006) и SMART (Greenfeld, Pavlichin, Mabuchi, & Herschlag, 2012)) и байесовские подходы (например, vbFRET (Bronson et al., 2009; Bronson et al., 2010) и ebFRET (van de Meent et al., 2014, 2013) ). Использование байесовских HMM имеет много преимуществ по сравнению с HMM максимального правдоподобия. Во-первых, в отличие от байесовских СММ, СММ максимального правдоподобия представляют собой фундаментально некорректные математические задачи — по сути, отдельные состояния могут «схлопываться» в отдельные точки данных, что приводит к сингулярности с бесконечной вероятностью, которой нет при разумной оценке СММ.Во-вторых, как мы обсудим в следующем разделе, байесовские подходы естественным образом включают в себя точность, с которой определенный объем данных может определять параметры СММ, путем изучения распределения вероятностей переходов вместо поиска одного набора вероятностей переходов. Помимо обеспечения точности, это позволяет комбинировать результаты нескольких отдельных молекул и одновременно получать консенсус, стохастические константы скорости из ансамбля отдельных молекул.В-третьих, в то время как подходы максимального правдоподобия могут привести к значительному переоснащению HMM и, следовательно, переоценке количества скрытых состояний, присутствующих в траектории сигнала, байесовские подходы по своей сути способны выбрать правильное количество скрытых состояний, присутствующих в траектории сигнала. Например, с HMM максимального правдоподобия лучшая оценка HMM траектории сигнала получается просто путем добавления дополнительных скрытых состояний; в крайнем случае для каждой точки данных будет одно скрытое состояние.Хотя HMM в этом крайнем случае идеально соответствовала бы данным, она не имела бы большого смысла и не была бы полезной моделью для предсказания будущего поведения системы. Хотя было предложено использовать эвристические подходы, такие как информационные критерии Байеса и Акаике (BIC и AIC соответственно), чтобы помочь выбрать правильное количество состояний в HMM максимального правдоподобия, они являются приближениями к истинным байесовским подходам, которые действительны только при определенные условия и то, что на практике мы обнаружили, не очень хорошо подходят для анализа данных smFRET на основе HMM.Кроме того, было показано, что байесовские HMM более точны, чем HMM максимального правдоподобия, для анализа траекторий сигналов, где время пребывания, t с, в скрытых состояниях является переходным по отношению к периоду измерения, τ (Бронсон и др. , 2009). Наконец, между подходом максимального правдоподобия и байесовским подходом к HMM фактически нет дополнительных вычислительных затрат, поскольку оба реализуют одни и те же алгоритмы для расчета вероятностей, связанных с HMM (например,г., алгоритм прямого-обратного), поэтому скорость не имеет значения. Учитывая преимущества байесовского подхода по сравнению с подходом максимального правдоподобия для HMM, мы рекомендуем использовать байесовские HMM при анализе траекторий сигналов из биофизических экспериментов с одной молекулой.

ХММ

Chemocare.com
Уход во время химиотерапии и после нее

Общее название : Альтретамин
Торговое название : Hexalen®
Другие названия : Гексаметилмеламин

Тип препарата: HMM является противораковым («противоопухолевым» или «цитотоксическим») химиотерапевтический препарат. HMM классифицируется как «алкилирующий агент». (Подробнее см. см. раздел «Как действует этот препарат» ниже).

Для чего используется HMM:

Примечание: Если лекарство одобрено для однократного применения, врачи могут выбрать использовать этот же препарат для решения других проблем, если они считают, что он может быть полезен.

Как дается ХММ:

• HMM принимают внутрь в виде капсул.
• HMM следует принимать после еды.
• Количество HMM, которое вы получите, зависит от многих факторов, в том числе от вашего рост и вес, общее состояние здоровья или другие проблемы со здоровьем, а также тип рак или состояние, которое лечат. Ваш врач определит дозу и расписание.

Побочные эффекты:

Важные вещи, которые следует помнить о побочных эффектах HMM:

• Большинство людей не испытывают всех перечисленных побочных эффектов.
• Побочные эффекты часто предсказуемы с точки зрения их начала и продолжительности.
• Побочные эффекты почти всегда обратимы и исчезнут после завершения лечения.
• Существует множество вариантов минимизации или предотвращения побочных эффектов.
• Нет никакой связи между наличием или тяжестью побочных эффектов и эффективность лекарства.
  

Следующие побочные эффекты являются общими (возникают более чем в 30%) для пациенты, принимающие HMM:

• Тошнота и рвота
• Потеря аппетита
• Диарея
• Низкие показатели крови.Ваши белые и красные кровяные тельца и тромбоциты могут временно уменьшаются, подвергая вас повышенному риску инфекции, анемии и/или кровотечения.

Эти побочные эффекты являются менее распространенными побочными эффектами (возникают примерно у 10-29%) пациентов, получающих HMM:

• Периферическая невропатия: (онемение и/или покалывание пальцев рук и/или ног).
• Спазмы желудка (см. боль в животе).
• Головокружение, сонливость или слабость (см. Центральная нейротоксичность).
• Депрессия, возбуждение, изменения настроения.

Не все побочные эффекты перечислены выше. Некоторые из них встречаются редко (происходят менее 10% пациентов) здесь не указаны. Тем не менее, вы всегда должны информировать поставщика медицинских услуг, если вы испытываете какие-либо необычные симптомы.

Когда обращаться к врачу или поставщику медицинских услуг:

Немедленно свяжитесь со своим поставщиком медицинских услуг , днем ​​или ночью, если вы должен возникнуть любой из следующих симптомов:

• Лихорадка 100.4°F (38°C) или выше, озноб (возможные признаки инфекции).

Следующие симптомы требуют медицинской помощи, но не являются неотложными. Свяжитесь со своим поставщиком медицинских услуг в течение 24 часов после того, как заметите любой из следующие:

• Тошнота (мешает приему пищи и не проходит при приеме назначенных лекарств)
• Рвота (рвота более 4-5 раз в сутки)
• Необычное кровотечение или синяк
• Черный или дегтеобразный стул или кровь в стуле или моче
• Диарея (4-6 эпизодов в сутки)
• Крайняя усталость (неспособность заниматься самообслуживанием)
• Чрезмерная сонливость или спутанность сознания

Всегда сообщайте своему лечащему врачу, если вы испытываете какие-либо необычные симптомы.

Меры предосторожности:

• Перед началом лечения HMM обязательно сообщите своему врачу о любых других лекарствах. вы принимаете (в том числе рецептурные, безрецептурные, витамины, растительные лекарственные средства, и т. д.). Не принимайте аспирин, продукты, содержащие аспирин, если только ваш врач специально не примет их. позволяет это.
• Не делайте никаких прививок или прививок без разрешения врача при приеме альтретамина.
• Сообщите своему лечащему врачу, если вы беременны или можете забеременеть до к началу этого лечения. Беременность категории D (альтретамин может быть опасен к плоду. Женщины, которые беременны или забеременеют, должны быть проинформированы о потенциальная опасность для плода.)
• Для мужчин и женщин: не зачинайте ребенка (забеременеть) при приеме альтретамина. Рекомендуются барьерные методы контрацепции, такие как презервативы.Обсудить с вашим врачом, когда вы можете безопасно забеременеть или зачать ребенка после терапии.
• Не кормите грудью во время приема этого лекарства

Советы по уходу за собой:

• Принимайте лекарства после еды – это уменьшает расстройство желудка.
• Вы можете быть подвержены риску заражения, поэтому старайтесь избегать скопления людей или людей с простудными заболеваниями и немедленно сообщите о лихорадке или любых других признаках инфекции своему лечащему врачу.
• Часто мойте руки.
• Для лечения/предотвращения язв во рту используйте мягкую зубную щетку и полощите ее три раза в день. день с 1/2 до 1 чайной ложки пищевой соды и/или соли, смешанной с 8 унциями воды.
• Используйте электрическую бритву и мягкую зубную щетку, чтобы минимизировать кровотечение.
• Избегайте контактных видов спорта или действий, которые могут привести к травме.
• Чтобы уменьшить тошноту, принимайте противорвотные препараты, назначенные врачом, и есть часто и небольшими порциями.
• Избегайте пребывания на солнце. Используйте солнцезащитный крем SPF 15 (или выше) и защитную одежду.
• Избегайте вождения и задач, требующих бдительности, до тех пор, пока вы не отреагируете на этот препарат. хорошо понимается.
• В целом употребление алкогольных напитков следует свести к минимуму или избегать полностью. Вам следует обсудить это со своим врачом.
• Больше отдыхайте.
• Следите за правильным питанием.
• Если вы испытываете симптомы или побочные эффекты, обязательно обсудите их со своим здоровьем. команда по уходу. Они могут назначить несколько лекарств, которые помогут вам переносить эти побочные эффекты, значительно уменьшают их воздействие и улучшают ваше самочувствие.

Мониторинг и тестирование:

Пока вы принимаете альтретамин, вы будете регулярно проверяться врачом. следить за побочными эффектами и проверять свою реакцию на терапию.Периодическая работа с кровью для контроля общего анализа крови (CBC), а также функции других органов (таких как ваши почки и печень) также будет заказан вашим врачом.

Как работает ХММ:

Химиотерапия (противоопухолевые препараты)
Раковые опухоли характеризуются делением клеток, которое больше не контролируется как в нормальной ткани. «Нормальные» клетки перестают делиться, когда приходят в контакте с подобными клетками, механизм, известный как контактное ингибирование.раковый клетки теряют эту способность. Раковые клетки больше не имеют нормальных проверок и балансы, которые контролируют и ограничивают деление клеток. Процесс клетки деление нормальных или раковых клеток происходит через клеточный цикл. То клеточный цикл проходит от фазы покоя через фазы активного роста, а затем к митозу (делению).

Способность химиотерапии убивать раковые клетки зависит от ее способности останавливать деление клеток.Обычно лекарства работают, повреждая РНК или ДНК, которые сообщают ячейка, как копировать себя в делении. Если клетки не могут делиться, они умирают. Чем быстрее делятся клетки, тем больше вероятность того, что химиотерапия убивает клетки, заставляя опухоль уменьшаться. Они также вызывают самоубийство клеток. (самогибель или апоптоз).

Химиотерапевтические препараты, воздействующие на клетки только во время их деления, называются препаратами клеточного цикла. конкретный.Химиотерапевтические препараты, воздействующие на клетки в состоянии покоя, называются клеточный цикл неспецифичен. График химиотерапии устанавливается в зависимости от тип клеток, скорость их деления и время действия данного препарата. вероятно, будет эффективным. Вот почему химиотерапию обычно проводят циклами.

Химиотерапия наиболее эффективна для уничтожения быстро делящихся клеток. К сожалению, химиотерапия не знает разницы между раковыми клетками. и нормальные клетки.«Нормальные» клетки вырастут снова и будут здоровыми, но в тем временем возникают побочные эффекты. «Нормальные» клетки чаще всего поражаются химиотерапией являются клетки крови, клетки во рту, желудке и кишечнике, и волосяные фолликулы; что приводит к низким показателям крови, язвам во рту, тошноте, диарее, и/или выпадение волос. Различные препараты могут воздействовать на разные части тела.

Альтретамин классифицируется как алкилирующий агент.Алкилирующие агенты наиболее активна в фазе покоя клетки. Эти препараты неспецифичны для клеточного цикла. Существует несколько типов алкилирующих агентов.

• Производные иприта: Мехлорэтамин, Циклофосфамид, Хлорамбуцил, Мелфалан и Ифосфамид.
• Этиленимины: Тиотепа и гексаметилмеламин.
• Алкилсульфонаты: Бусульфан.
• Гидразины и триазины: Альтретамин, прокарбазин, дакарбазин и Темозоломид.
• Нитромочевины: Кармустин, ломустин и стрептозоцин. Нитромочевины уникальны, потому что, в отличие от большинства химиотерапевтических препаратов, они могут проникать через кровь и мозг. барьер. Они могут быть полезны при лечении опухолей головного мозга.
• Соли металлов: Карбоплатин, Цисплатин и Оксалиплатин.

Примечание: Мы настоятельно рекомендуем вам поговорить со своим лечащим врачом. о вашем конкретном заболевании и лечении. Информация, содержащаяся на этом веб-сайте предназначено быть полезным и образовательным, но не заменяет для медицинской консультации.

Chemocare.com предназначен для предоставления самой последней информации о химиотерапии пациентам и их семьям, опекунам и друзьям.Для получения информации о 4-й программе наставничества ангелов посетите сайт www.4thangel.org

Ковбои вырезают Джейлона Смита, которому осталось всего два года до того, чтобы стать профессиональным игроком в боул LB

Время от времени в НФЛ происходят неожиданные сокращения, и это привлекает мое внимание.

А еще есть один, который заставляет меня идти хммм :

Сезонный сюрприз: согласно источнику, Cowboys выпустили LB Джейлона Смита.

— Адам Шефтер (@AdamSchefter) 6 октября 2021 г.

Адам Шефтер из ESPN сообщает, что «Ковбои» освобождают полузащитника Джейлона Смита.Шефтер описывает это как сезонную неожиданность, и, честно говоря, я и сам не мог бы выразиться лучше.

26-летнему Смиту осталось два года до того, как стать профессиональным боулером. А год назад коллеги Смита из НФЛ назвали его одним из 100 лучших игроков (88-е место в общем зачете). Начало кампании 2021 года не было благоприятным для Смита. За четыре игры средний полузащитник имеет 0 сэков, 0 отборов на поражение и 0 ударов квотербека. Смит сыграл всего 56% снэпов в обороне «Далласа», что является резким падением, если учесть, что он участвовал в более чем 90% снэпов команды в каждом из трех предыдущих сезонов. Ковбои все еще должны Смиту более 7 миллионов долларов зарплаты, поэтому им не должно нравиться то, что они видят на данный момент. Но любая команда, подписавшая Смита, может получить выгоду от подписания игрока со скидкой, в то время как Даллас выплачивает солидный кусок. Следовательно, наблюдать за тем, как Смит попал в проволоку, интересно.

Как бы то ни было, Смит занимает 11-е место среди полузащитников Pro Football Focus после четырех недель. Оценка Смита 69,5 лучше, чем у Бобби Вагнера (69,1), Фреда Уорнера (57,5) и Рокуана Смита (46,9).PFF также высоко оценивает усилия Смита по освещению. Уровень охвата Смита 82,2 — третий среди полузащитников. Учитывая этот набор данных, теперь я еще больше запутался, почему Даллас отказывается от Смита.

Поскольку Смит — известная личность, он учился в известном университете (Нотр-Дам) и постоянно оставлял команду под пристальным вниманием (Ковбои), найдутся те, кто захочет, чтобы Медведи надрали ему шины. Итак, давайте обсудим это на мгновение.

Какая-то часть меня не уверена, насколько подходит эта команда.С Алеком Оглетри, исполняющим роль замены, и Дэнни Треватаном, возвращающимся из IR, я не уверен, где Чикаго может втиснуть Смита в эту защиту. Но с другой стороны, этот уровень покрытия 82,2 выделяется. Объединение Рокуана Смита с более молодым игроком, обладающим интригующей родословной, может стоить того, чтобы бросить кости. И если «Медведи» смогут улучшиться в этой области с добавлением в середине сезона, это будет не самое худшее, что может случиться.

SVM-HMM: Маркировка последовательности с помощью SVM

Тегирование последовательностей с помощью машин структурных опорных векторов

и его применение для тегирования частей речи

Эван Хербст, Торстен Йоахимс
Корнельский университет
[evh5 Корнелл Эду] [tj cs Корнелл Эду]

Введение

y = argmax _y {Σ _{i = 1. .l} (x _i • w _{y i} ) + φ _транс (y _i-1 ,y _i ) • w _транс }.

SVM ^hmm изучает один весовой вектор w _y для каждого тега y и одного вектора весов w _trans для весов перехода между соседними тегами. φ _транс (y _i-1 , y _i ) является вектором-индикатором, который имеет ровно одну запись, установленную в 1, соответствующую пара y _i-1 ,y _i .Обратите внимание, что в отличие от обычного HMM, наблюдения x ₁ …x _l могут быть естественным образом выражены в виде векторов признаков, а не только в виде атомарных токенов. В течение обучение, SVM ^hmm решает следующую задачу оптимизации с учетом обучения примеры ( x ¹ ,y ¹ ) … ( x ⁿ ,y ⁿ ) последовательностей векторов признаков с их правильными последовательностями тегов. Как потеря функция Δ(y ⁱ ,y), используется количество ошибочно классифицированных тегов в предложении.

        мин. w*w + C/n Σ _{i = 1..n} ξ _i
         с.т. для всех у: [Σ _{i = 1..l} (x ¹ _i • w _{y ¹ i} ) + φ _транс (y ¹ _i-1 ,y ¹ _i ) • w _транс ] >= [Σ _{i = 1..l} (x ¹ _i • ш _и ) + φ _транс (y _i-1 ,y _i ) • w _транс ] + Δ(у ¹ ,у) — ξ _1
…
                   для всех у: [Σ _{i = 1..l} (x ⁿ _i • w _{y ⁿ i} ) + φ _транс (y ⁿ _i-1 ,y ⁿ _i ) • w _транс ] >= [Σ _{i = 1..l} (x ⁿ _i • ш _и ) + φ _транс (y _i-1 ,y _i ) • w _транс ] + Δ(y ⁿ ,y) — ξ _n

C — это параметр, который балансирует между размером маржи и ошибкой обучения. Пока это проблема имеет экспоненциально много ограничений, мы используем алгоритмы секущих плоскостей, реализованные в SVM ^struct , чтобы решить эту проблему. задача с точностью до ε за полиномиальное время [Tsochantaridis и другие. 2004, Цочантаридис и др. 2005]. В частности, мы используем постановка учебных задач введена в SVM ^struct V3.00, что делает эту версию SVM ^hmm значительно быстрее, чем предыдущие версии.

Более подробная информация о SVM ^struct доступна здесь.

Исходный код и двоичные файлы

http://download.joachims.org/svm_hmm/v2.13/svm_hmm.tar.gz

Распакуйте соответствующий архив, который вы скачали с помощью

смола -xzf svm_hmm.tar.gz

сделать

SVM ^хмм не компилируется под MS Visual C, как написано. SVM ^hmm использует расширение SGI hash_map для STL, а также некоторые другие менее важные расширения. Если у вас нет совместимого с SGI STL (скорее всего, у вас есть, если вы используете любой Linux), вы можете получить его с http://www.sgi.com/tech/stl/download. html, хотя их может не компилироваться для вас без подгонки. Если вы хотите скомпилировать SVM ^hmm под MS Visual C, вам также потребуется создать проект.Гораздо проще для компиляции в Windows использовать MinGW или Cywin.

Как использовать

svm_hmm_learn_hideo -c -e training_input.dat файл_модели.dat
svm_hmm_classify test_input.dat файл модели.dat classify.tags

• — параметр, используемый для взвешивания резервного члена в формулировке SVM по отношению к члену весового вектора. ПРИМЕЧАНИЕ. В отличие от версии 1.01, значение C делится на количество обучающие примеры. Таким образом, чтобы получить результаты, эквивалентные V1.01, умножьте C по количеству обучающих примеров.
• — точность, с которой требуются ограничения удовлетвориться решением. Меньший ЭПСИЛОН, чем дольше и больше занимает тренировка памяти, тем точнее решение. Однако решения с большей точностью, чем 0,5, обычно не улучшают прогноз. точность. training_input.dat и test_input.dat — это файлы, содержащие обучающие и тестовые примеры. Они имеют формат, указанный ниже для входных файлов.
• modelfile.dat содержит информацию о модели SVM ^hmm , полученную из входных данных.Модель SVM ^struct записывается в файл modelfile_svmModel.dat. SVM-модель файл имеет расширение .dat независимо от расширения файла модели.
• classify.tags получит списки тегов, предсказанных для тестовых примеров, т.е. для каждого тестовый пример, classify.tags будет содержать что-то вроде {TAG1 TAG2 TAG3}}. Нет или больше пробелов между соседними комплекты кронштейнов.

Формат входного файла

TAG qid:EXNUM.INDEX FEATNUM:FEATVAL FEATNUM:FEATVAL … #комментарий здесь
…

PRON четыре раза в день:1.1 1:1 2:1 3:1 #см.
СУЩЕСТВИТЕЛЬНОЕ qid:1.2 4:1 5:1 #джейн
ГЛАГОЛ qid:1.3 2:-1 6:1 7:2.5 #play
ГЛАГОЛ qid:1.4 3:-1 8:1 #мяч
СУЩЕСТВИТЕЛЬНОЕ qid:1.5 9:1 10:1 #.
PRON четыре раза в день: 2,1 3:1 11:1 12:1 #она
ГЛАГОЛ qid:2.2 1:-1 13:1 14:2 #is
JJ четыре раза в день: 2,3 15:1 16:0,1 17:-1 #хорошо
ПЕРИОД qid:2. 4 9:0.5 18:1 #.

TAG может быть любым токеном без пробела, кроме специального тега «~NONE~» (без кавычек), который зарезервирован для использования с марковские модели более высокого порядка (запланированное расширение в будущем).

Пример проблемы

Вы найдете пример набора данных POS-тегов по адресу

http://скачать.joachims.org/svm_hmm/examples/example6.tar.gz

Загрузите этот файл в каталог svm_hmm и распакуйте его с помощью

gunzip -c example6.tar.gz | смола xvf-

Будет создан подкаталог example6. Попробуйте следующее:

./svm_hmm_learn -c 5 -e 0.5 пример6/декларация_независимости.шина декларация.модель
 
./svm_hmm_classify example6/gettysburg_address.shin Declaration.model test.outtags
 

кот Declaration_of_independence.shin | awk ‘{печать $NF}’ | сортировать | уник > декл.слова
 
cat gettysburg_address.shin | awk ‘{печать $NF}’ | сортировать | уникальный > gett.words
 
comm -1 -3 decl.words gett.words | туалет -л
77

wc -l gettysburg_address.shin
289

Отказ от ответственности: этот пример не был помечен с профессиональной точностью; не используй это для любых реальных экспериментов.Мои теги в Геттисберге основаны на документе http://faculty.washington.edu/dillon/GramResources/gettysburgtreetagger.html, который был помечен тегером Шмида, но TreeTagger, вероятно, сначала был обучен на реальном корпусе.

Известные проблемы

• На 64-разрядных машинах AMD и Intel могут возникать проблемы с точностью при использование алгоритмов w3 или w4 для задач со многими функциями. Чтобы исправить это проблемы, измените «#define CFLOAT» на «двойной» в svm_common.h. Спасибо тебе Chih-Jen Lin за указание на это.
• Ядро RBF повреждено.

История

V1.01 — V2.13

• Новый алгоритм обучения, основанный на эквивалентной переформулировке 1-slack проблема с обучением. Это делает обучение на линейном ядре на несколько порядков быстрее. величина быстрее, чем в V1.01. См. изменения, внесенные SVM ^struct V3.00 для общего свойства нового структурного алгоритма обучения SVM.
• Новые подпрограммы ввода-вывода, быстрее для чтения больших данных и файлов моделей.
• Исходный код для SVM ^хм V1.01.

V1.00 — 1.01

•  Исправлена ​​небольшая ошибка, связанная с сообщением об отладке «Есть вероятно, ошибка в ‘find_most_violated_constraint_*’. .’.

Каталожные номера

• И. Цочантаридис, Т. Иоахимс, Т. Хофманн и Ю. Алтун, Большое поле Методы структурированных и взаимозависимых выходных переменных, Журнал Исследование машинного обучения (JMLR), 6 (сентябрь): 1453–1484, 2005 г.
  [PDF]  
• И. Цочантаридис, Т. Хофманн, Т. Йоахимс, Ю. Алтун. Машинное обучение опорных векторов для взаимозависимых и структурированных Выходные пробелы . Международная конференция по машинному обучению (ICML), 2004 г.
  [Постскриптум]  [PDF]
• Ю. Алтун, И. Цочантаридис, Т. Хофманн, Скрытый марковский опорный вектор Машины . Международная конференция по машинному обучению (ICML), 2003 г.

Ускоренный поиск профилей HMM

Введение

Поиск гомологии в базе данных последовательностей является одним из наиболее важных приложений в вычислительной молекулярной биологии.Последовательности генома быстро приобретаются для постоянно расширяющегося набора видов. Чтобы максимально использовать данные о последовательностях, мы хотим максимизировать мощность вычислительных инструментов сравнения последовательностей, чтобы обнаружить отдаленные гомологии между этими последовательностями, чтобы узнать ключи к разгадке их функций и истории эволюции. Наиболее широко используемым инструментом для сравнения последовательностей и поиска в базе данных является BLAST [1]–[3].

С момента появления BLAST в теории сравнения последовательностей были достигнуты некоторые важные успехи, в частности, за счет использования вероятностных методов вывода, основанных на скрытых марковских моделях профиля (профильные HMM) [4].Подходы к вероятностному моделированию обеспечивают согласованную основу для параметризации сложных позиционно-специфических моделей сохранения и эволюции последовательностей [5]. В свете этих достижений в BLAST были внесены многочисленные улучшения [6]–[9]. По сути, однако, реализация BLAST вычисляет оптимальные оценки локального выравнивания, используя специальных штрафов за пропуски . Это ядро ​​реализации может быть не легко адаптировано к вероятностной модели вставки/удаления и более мощному алгоритму HMM «вперед/назад», который вычисляет не только одно наиболее подходящее выравнивание, но и сумму вероятностей по всему ансамблю локального выравнивания.Алгоритм «Прямой» позволяет назначать более мощную и формальную логарифмическую статистику правдоподобия для каждой целевой последовательности, а «Прямой/Назад» позволяет назначать значения достоверности для каждого выровненного остатка.

Тем не менее, несмотря на какие-либо привлекательные преимущества HMM, ни одна реализация полностью вероятностных методов сравнения последовательностей еще не приблизилась к полезности BLAST. Наиболее широко используемые реализации профильной технологии HMM, в том числе HMMER из моей лаборатории, были медленными и требовательными к вычислительным ресурсам, примерно в 100–1000 раз медленнее, чем BLAST для поиска сопоставимого размера.В эпоху огромных баз данных последовательностей этот недостаток скорости перевешивает любое преимущество методов HMM. Профильные методы HMM стали важными только в нише анализа семейств белковых доменов, где разница в скорости компенсируется возможностью использовать один профиль HMM для представления семейства сотен гомологичных отдельных последовательностей [10], [11].

HMMER был целью многих усилий по ускорению и оптимизации [12]–[15], но эти усилия имели ограниченный эффект.Единственными ускорениями, в которых сообщается о большом выигрыше, являются реализация собственных алгоритмов динамического программирования HMMER на специализированном оборудовании, включая FPGA (программируемые пользователем вентильные матрицы) [16]–[19], СБИС ASIC (микросхемы специального назначения), GP-GPU (общие целевые графические процессоры) [20], [21] и большие многопроцессорные кластеры [22], [23]. Было предпринято меньше усилий для разработки быстрых алгоритмов HMM с эвристическим профилем для стандартных массовых процессоров [24]–[26] способами, сравнимыми с тем, как BLAST эвристически аппроксимирует и ускоряет оптимальное согласование динамического программирования Смита/Уотермана [27]. Проблема состоит в том, что для сохранения значительного, но незначительного прироста чувствительности, который демонстрируют методы профильного HMM по сравнению с BLAST [28]–[30], любая полезная эвристика ускорения профильного HMM должна быть более чувствительной, чем уже превосходная эвристика BLAST.

Еще одна причина ограниченного воздействия предыдущих усилий по ускорению заключается в том, что они были почти исключительно сосредоточены на ускорении оптимального алгоритма оценки локального выравнивания (известного в литературе как алгоритм Витерби) в отличие от более предпочтительного алгоритма Forward.Отчасти это связано с тем, что алгоритмы оптимального локального выравнивания более известны, а отчасти потому, что предыдущие версии самого HMMER реализовывали оценку Витерби, а не оценку вперед. Форвардные реализации примерно в 3-9 раз медленнее, чем реализации Витерби, а ожидаемое статистическое распределение оценок Форвард для профильных HMM не было достаточно хорошо изучено, чтобы назначать точные E-значения (значения ожидания). Недавно я описал удовлетворительное решение последней проблемы [31], которое оставляет проблему ускорения.

Здесь я описываю конвейер эвристического ускорения, реализованный HMMER3, переработанной версией программного обеспечения HMMER. По сравнению с предыдущей версией HMMER, HMMER3 примерно в 100 раз быстрее из-за использования нового эвристического алгоритма, называемого фильтром MSV, а также значительно мощнее, потому что он переходит от оптимального локального выравнивания Витерби к полной прямой/обратной оценке. ансамблей выравнивания, используя больше математических преимуществ вероятностного моделирования.Таким образом, HMMER3 теперь примерно так же быстр, как BLAST, расширяя при этом преимущества производительности профильных методов HMM.

Результаты

Обзор

Основной алгоритм, ускоряющий HMMER3, называется MSV, что означает множественный (локальный, неразрывный) сегмент Витерби. Он был вдохновлен техникой, используемой в ParAlign [32]. Как показано на рис. 1, модель MSV представляет собой неразрывную версию модели локального выравнивания множественных попаданий HMMER3. Вероятностная модель многократного локального выравнивания без пробелов MSV достигается простым игнорированием переходов состояния совпадения, удаления и вставки исходного профиля и неявной обработкой переходов совпадения-совпадения как 1.0.

Рис. 1. Профиль MSV.

A: Архитектура профиля HMM, используемая HMMER3 [4], [5], [31]. Области, гомологически выровненные с запросом, представлены линейной базовой моделью, состоящей из согласованных позиций (в этом примере ), каждая из которых состоит из совпадения, удаления и состояния вставки (показанных в виде прямоугольников с пометкой M, кружков с пометкой D и ромбов). отмечены I), связанные вероятностями переходов состояний (стрелки). Состояния совпадения несут вероятности эмиссии для конкретной позиции для подсчета остатков в каждой согласованной позиции.Состояния вставки испускают остатки с вероятностью испускания, идентичной фоновому распределению. Дополнительные фланкирующие состояния (обозначенные N, C и J) выделяют ноль или более остатков из фонового распределения, моделируя негомологичные области, предшествующие, следующие или присоединяющиеся к гомологичным областям, выровненным по базовой модели. Начальное (S), начальное (B), конечное (E) и конечное (T) состояния не излучаются. B: Профиль MSV формируется путем неявной обработки всех вероятностей перехода совпадение-совпадение как 1,0. Это соответствует виртуальному удалению состояний удаления и вставки.Остальные параметры профиля остаются прежними. Эта модель генерирует последовательности, содержащие один или несколько сегментов локального выравнивания без пропусков. Обратите внимание, что обе модели кажутся неправильно нормализованными; например, каждое состояние совпадения в модели MSV имеет локальный выходной переход с вероятностью 1,0 (оранжевые стрелки) в дополнение к переходу совпадение-совпадение с вероятностью 1,0. Это связано с уловкой, используемой для установления однородного локального распределения длин фрагментов, в котором эти профили являются свернутыми представлениями гораздо большей (и должным образом нормализованной) «неявной вероятностной модели», как объяснено в [31]. C: Пример того, как может выглядеть выравнивание более крупного профиля MSV (длиной ) с целевой последовательностью (длиной ), как путь через матрицу динамического программирования (DP). Здесь модель идентифицирует два сегмента выравнивания без пропусков с высокой оценкой (черные точки, указывающие на остатки, выровненные по состояниям соответствия профиля), и присваивает все остальные остатки состояниям N, J и C в модели (оранжевые точки; «неиспускающее состояние или переход состояния»). Обратите внимание, что диагонали без зазоров не обязательно должны соответствовать одному выравниванию с зазорами.

https://doi.org/10.1371/journal.pcbi.1002195.g001

Оценка MSV по сути аналогична «суммарной оценке» BLAST для одного или нескольких неразрывных HSP (пар с высокой оценкой). Отличие состоит в том, что MSV не требует согласованности выравнивания (два выравнивания без пробелов не обязательно должны быть согласованы с одним выравниванием с пробелами). В эвристике фильтрации это различие не имеет значения. HMMER3 вычисляет оценку MSV непосредственно с помощью динамического программирования, минуя эвристики BLAST, связанные со словом и расширением совпадений.

Тот факт, что MSV по существу обходит две основные эвристики BLAST, дает интуитивно понятный аргумент в пользу того, что оценки MSV должны быть более чувствительными в целом эвристиками, чем подход BLAST. Однако я не пытался строго сравнивать производительность эвристики HMMER MSV с другими эвристиками ускорения, например, в BLAST или FASTA.

Реализация HMMER3 использует несколько синергетических статистических и вычислительных функций модели MSV.Я резюмирую эти функции здесь, прежде чем описывать их подробно:

• Показатели выравнивания MSV могут быть эффективно рассчитаны с использованием так называемых «полосатых» векторно-параллельных методов, первоначально разработанных для локального выравнивания последовательностей Smith/Waterman [33], поскольку модель MSV удаляет состояния делеции и вставки, которые мешают векторному параллелизму.
• Поскольку модель MSV дает предсказуемое распределение оценок для негомологичных последовательностей, при этом оценки ограничены узким диапазоном, который в значительной степени не зависит от характеристик запроса и целевой последовательности, значения MSV могут быть аппроксимированы с пониженной точностью (8 битов, в диапазоне оценок от 0 до 255).Это обеспечивает 16-кратный векторный параллелизм в современных массовых процессорах со 128-битными векторными регистрами.
• Модель MSV остается полностью вероятностной моделью локального выравнивания, поэтому показатели MSV подчиняются предположениям об ожидаемом распределении Гумбеля вероятностных показателей локального выравнивания [31]. Это позволяет быстро рассчитать P-значения.
• Поскольку мы можем рассчитать P-значения MSV, мы можем использовать оценки MSV в качестве настраиваемого и селективного фильтра последовательности. Если целевая последовательность имеет оценку MSV с P-значением меньше выбранного порога, мы передаем всю последовательность более точным и ресурсоемким алгоритмам оценки. По определению порог P-значения представляет собой долю негомологичных последовательностей, которые, как ожидается, пройдут фильтр.

Фильтр MSV представляет собой эвристическое ускорение, не гарантирует нахождение всех целей с высокими показателями. Общая производительность конвейера ускорения HMMER3 с точки зрения скорости, специфичности и чувствительности зависит от нескольких проблем и компромиссов, в том числе от того, насколько быстры фильтры, насколько точно и быстро можно оценить P-значения для оценок фильтра и установлен ли порог для MSV. P-значения могут быть установлены для удаления большинства негомологов при удалении нескольких истинных гомологов, если таковые имеются, которые были бы обнаружены при нефильтрованном поиске.Это эмпирические вопросы, на которые я ответил с помощью сравнительных экспериментов.

Следующие разделы, особенно о распараллеливании векторов и обеспечении того, чтобы оценки можно было хранить в ограниченных числовых диапазонах, неизбежно являются техническими и краткими. При первом чтении читатель может захотеть пропустить или просмотреть раздел «Конвейер ускорения HMMER3», чтобы увидеть, как эти технические аспекты вписываются в общую схему и как работает эта схема ускорения.

Модель MSV: обозначения и параметризация

Оценка MSV для целевой последовательности представляет собой стандартную оценку HMM Viterbi, логарифмическую оценку отношения правдоподобия одного оптимального (максимально вероятного) выравнивания: отношение вероятности оптимального выравнивания ° для заданной модели MSV и вероятности последовательности учитывая модель нулевой гипотезы: для запроса позиций длины профиль MSV имеет соответствующие параметры эмиссии (где размер алфавита, 4 нуклеотида или 20 аминокислот), а также дополнительные параметры перехода состояния, включающие фланкирующие N, B, E, C , и состояния J, которые объясняют негомологичные остатки.Другие переходы между состояниями в исходном профиле игнорируются, что означает, что переходы «совпадение-совпадение» неявно обрабатываются как 1. 0.

Предполагается, что нулевая модель представляет собой HMM с одним состоянием, излучающим остатки с фоновыми частотами (т. е. стандартная нулевая модель i.i.d.: независимые, одинаково распределенные остатки) с распределением геометрической длины, заданным параметром перехода .

Оценки совпадения для конкретной позиции предварительно вычисляются как логарифмические отношения шансов для остатка, испускаемого из состояния совпадения M с вероятностью эмиссии, по сравнению с фоновыми частотами нулевой модели: Эти оценки совпадения (а также вероятности эмиссии и фоновые частоты) являются так же, как в исходном профиле.

Единственными параметрами перехода состояния в модели MSV являются те, которые управляют моделированием длины целевой последовательности, однородным распределением длины фрагментов локального выравнивания и количеством попаданий в основную модель гомологии на целевую последовательность [31]. Они также идентичны параметризации исходного профиля [31]. В частности, они установлены следующим образом для целевой последовательности остатков длины и модели консенсусных положений длины:

Моделирование длины целевой последовательности:

Равномерное распределение длины фрагментов локального выравнивания:

Несколько попаданий в цель:

Алгоритм оценки MSV: векторное распараллеливание SIMD

Алгоритм MSV хорошо подходит для векторного распараллеливания с использованием стандартных инструкций SIMD (одна инструкция, несколько данных), таких как инструкции Streaming SIMD Extensions (SSE) в Intel-совместимых системах и инструкции Altivec/VMX в системах PowerPC.Эти наборы векторных инструкций используют 128-битные векторы для вычисления до 16 одновременных операций.

Описано несколько векторных методов для ускорения классического локального выравнивания последовательностей Смита/Уотермана [34], [35], а методы ускорения рекурсий динамического программирования Смита/Уотермана (DP) легко адаптируются для профилирования HMM. Удивительно эффективный векторно-параллельный подход, названный полосатым Smith/Waterman, был описан Фарраром [33].

Чередование решает проблему шаблона зависимости данных в рекурсиях динамического программирования в стиле Смита/Уотермана.Расчет каждой ячейки в решетке динамического программирования требует наличия предварительно рассчитанных ячеек , и . В векторизованной по строкам реализации отдельные ячейки (обычно 4, 8 или 16) хранятся в каждом отдельном векторе, так что каждая строка векторизованной матрицы DP хранит ячейки в векторах Q с номерами , где . В подходе Фаррара клетки непоследовательно назначаются векторам в виде полосатого рисунка (рис. 2). В полосатых векторах, когда мы вычисляем набор из нескольких ячеек, содержащихся в одном векторе в текущей строке, все необходимые нам предыдущие диагональные ячейки аккуратно доступны в правильном порядке в векторе в предыдущей строке, а ячейки выше находятся в вектор .Чередование сводит к минимуму дорогостоящие операции, такие как сдвиг или перестановка значений ячеек внутри векторов. Недостатком является то, что расчеты путей удаления (зависящие от ячеек слева) могут потребовать полной сериализации. Фаррар описал эффективные методы минимизации этой проблемы. В алгоритме MSV, поскольку вычисляются только диагонали без пропусков, этого недостатка полностью избегают. Основная идея того, как работает индексирование с чередованием, схематично представлена ​​на рис. 2.

Рис. 2. Иллюстрация чередующейся индексации для векторных вычислений SIMD.

В верхней строке (пурпурный контур) показана одна строка решетки динамического программирования для модели длиной . Если взять пример векторов, каждый из которых содержит клетки, то 14 клеток содержатся в векторах с номерами . (Две неиспользуемые ячейки, помеченные x, устанавливаются в контрольное значение.) В рекурсии динамического программирования, когда мы вычисляем каждую новую ячейку в новой строке, мы получаем доступ к значению в ячейке в предыдущей строке. При индексации с чередованием вектор содержит ровно четыре ячейки, необходимые для вычисления четырех ячеек в новом векторе в новой строке матрицы динамического программирования (бирюзовый контур). Например, когда мы вычисляем ячейки в векторе, мы получаем доступ к вектору предыдущей строки, который содержит нужные нам ячейки в том порядке, в котором они нам нужны (пунктирные линии и прямоугольник). Если вместо этого мы проиндексировали ячейки в векторы очевидным образом, в линейном порядке (в векторе и так далее), такого соответствия с четырьмя нет, и каждое вычисление нового вектора потребовало бы дорогостоящего вмешательства в порядок ячеек в векторах предыдущей строки. При чередующемся индексировании требуется только одна операция сдвига для каждой строки вне самого внутреннего цикла: последний вектор в каждой законченной строке сдвигается вправо (mpv, серого цвета с индексами красных ячеек) и используется для инициализации вычисления следующей строки.

https://doi.org/10.1371/journal.pcbi.1002195.g002

Чтобы максимизировать параллелизм, я реализовал MSV как 16-кратное параллельное вычисление со значениями оценок, хранящимися в виде 8-битных целых чисел без знака, ограниченных диапазоном 0‥255. При этом используется тот факт, что оценки локального выравнивания в вероятностной модели HMMER3 имеют узкий и предсказуемый динамический диапазон, что позволяет проводить численный анализ стабильности, который оправдывает использование пониженной точности. (Подробности этого анализа приведены в следующем разделе.) Это изменение масштаба определяется тремя значениями (базовое, смещение и масштаб), где «базовое» — это начальное смещение от нуля, чтобы сделать оценки MSV неотрицательными (по умолчанию: 190), «масштабное» — коэффициент масштабирования (по умолчанию 3, поэтому Оценки MSV выражены в единицах одной трети битов), а «смещение» представляет собой смещение оценок отдельных остатков, используемое для того, чтобы сделать все оценки отдельных остатков беззнаковыми затратами байтов относительно максимальной оценки остатка. Используя термины масштаба и систематической ошибки, оценки остатков для конкретных позиций преобразуются в предварительно вычисленные масштабированные затраты (насыщаются при максимальной стоимости 255) и сохраняются в векторах в порядке чередования (рис. 2).Оценки перехода преобразуются в предварительно рассчитанные масштабированные затраты с помощью (насыщение при максимальной стоимости 255).

Чтобы определить SIMD-рекурсию MSV, я буду использовать пять векторных инструкций псевдокода для операций над битовыми целыми числами (в нашей реализации), либо скалярами, либо векторами, содержащими битовые целые элементы с номерами . Каждая из этих операций либо доступна, либо легко создается как в SSE, так и в Altivec/VMX:

В этом псевдокоде векторизованный алгоритм MSV выглядит следующим образом:

Инициализация:

Рекурсия:

Завершение:

Постоянный член -4.3 бита на шаге завершения возникает из-за аппроксимации, которая имеет дело с ошибкой округления при подсчете и стоимости перехода. Это объясняется в следующем разделе. Условие завершения предполагает, что , так что значения для состояния C такие же, как для состояния J (таким образом избавляя от необходимости вычислять значения состояния C в рекурсии).

Этот алгоритм реализован как для инструкций SSE, так и для инструкций Altivec/VMX в исходном коде HMMER3 в impl_{sse,vmx}/msvfilter.c::p7_MSVFilter().

Анализ последствий снижения численной точности

Этот раздел носит исключительно технический характер и может быть пропущен при первом чтении. При сужении динамического диапазона вычислений оценки до небольших целых чисел без знака мы должны убедиться, что ни опустошение, ни переполнение либо не происходят, либо не имеют ошибочных последствий. Мы также должны быть уверены, что величина любой накопленной ошибки округления допустима. Поскольку конвейер ускорения HMMER3 (описанный ниже) использует векторно-параллельные, чередующиеся реализации пониженной точности как алгоритма MSV (описанного выше), так и стандартного алгоритма Витерби (оптимального выравнивания) для исходной модели профиля с вставками/удалениями, следующий анализ учитывает как баллы MSV, так и баллы Витерби.

Для определения потери значимости мы используем тот факт, что существует нижняя граница показателей оптимального локального выравнивания в зависимости от длины модели и длины целевой последовательности. При наихудшем возможном оптимальном локальном выравнивании с положительной оценкой профиль ядра соответствует только одному состоянию совпадения с одним остатком с показателем , а остальные остатки целевой последовательности объясняются фланкирующими состояниями N и C. Таким образом, наихудший случай имеет логарифмическую оценку правдоподобия, которая составляет: Известные белковые последовательности могут иметь длину более 30 000 остатков (человеческий тайтин, например, составляет 34 350 а.о.).Если мы укажем в качестве проектных ограничений, мы можем предположить более низкую оценку битов для оптимального локального выравнивания.

Для управления переполнением мы используем тот факт, что мы будем использовать только реализацию с пониженной точностью в качестве фильтра для целевых последовательностей. Любая последовательность с выбранным порогом значения P будет передана более медленной процедуре для пересчета с полной точностью. Используя насыщенных арифметических инструкций, любые целевые последовательности, которые переполняются, будут оцениваться как максимально возможные.Теперь нам нужно только быть в состоянии гарантировать, что верхняя граница оценки имеет P-значение — самый низкий порог P-значения, который мы когда-либо планируем использовать. Из Милосаевича [31], [36] мы знаем консервативную оценку порога битовой оценки. Для расчетного предела, допускающего пороги фильтрации, достаточно верхнего предела оценки в 17 битов. (0,02 — это пороговое значение P по умолчанию для MSV, а 0,001 — это значение по умолчанию для баллов Витерби, как обсуждается ниже).

Этот диапазон от −60 до 17 бит применяется к полным оптимальным локальным выравниваниям; в отдельных ячейках расчета динамического программирования нам нужен чуть больший динамический диапазон. Например, выравнивание с высокой оценкой в ​​​​17 битов будет иметь оценку более 17 бит в последней ячейке, которая выравнивает состояние совпадения с гомологичным остатком, поскольку за этим состоянием всегда следуют отрицательные оценки из EC, CC и CT. переходы в оптимальном выравнивании. Принимая это во внимание (включая некоторые вопросы порядка оценки — тот факт, что вклады некоторых переходов, включая вклады нулевой модели, включаются в этап завершения после завершения рекурсии динамического программирования), можно показать, что диапазон — 61…21 бит достаточно, чтобы гарантировать, что ни одна ячейка DP, участвующая в оптимальном локальном выравнивании диапазона −60…17 бит, не будет переполнена или потеряна.

Эти же границы применимы как к исходной модели локального выравнивания (выравнивания Витерби со вставками и удалениями), так и к модели MSV, поскольку ни один шаг в установлении этих границ не требует учета вероятностей перехода в базовой модели (сопоставление, вставка и удаление). состояния).

Таким образом, нам нужен динамический диапазон 82 бита (-61 … 21 бит), а максимальный диапазон 8-битного целого числа составляет 256 значений, поэтому достаточно масштабирования логарифмических шансов до единиц 1/3 бита. (По совпадению, это сравнимо с масштабированием и округлением стандартных оценочных матриц, используемых BLAST или FASTA; например, BLOSUM45 имеет размерность 1/3 бита.) Затем используется «базовый» член смещения для настройки представленного диапазона значений в соответствии с диапазоном оценок битов. Для 8-битных целых чисел без знака основание +190 означает, что значения 0‥255 представляют диапазон битов.

Округление оценок до ближайшей 1/3 бита приводит к ошибке округления, равной биту на оцениваемый термин. Сумма независимых, одинаково распределенных случайных отклонений, равномерно распределенных на интервале, имеет нулевое среднее значение и дисперсию . Поскольку локальная оценка выравнивания для целевой последовательности длины моделируется как сумма условий оценки выбросов и переходов, даже если ошибка округления каждого члена была бы независимой и равномерно распределенной, накопленная ошибка округления была бы большой (нормально распределенной со средним нулем и дисперсией ; поэтому для накопленной ошибки будет иметь стандартное отклонение 2. 7 бит). Хуже того, ошибки округления не являются ни независимыми, ни равномерно распределенными. Особенно плохой случай связан с вероятностью перехода, близкой к 1,0, такой как большинство переходов «совпадение-совпадение» в исходной модели профиля с промежутками, где для всех достаточно больших раундов стоимость равна нулю. Другой плохой случай связан с состояниями HMM, которые имеют циклы, такие как переходы вставка-вставка, где ошибка округления умножается на количество посещений состояния. Эти два неблагоприятных случая делают автопетли, производящие цепочки состояний N, C, J или вставки, особенно проблематичными, потому что эти вероятности самоперехода часто близки к 1.0; целая цепочка из них часто оценивается как ноль, накапливая большую ошибку округления.

Модель MSV и ее реализация используют несколько функций для уменьшения ошибки округления до допустимых пределов. Во-первых, исключая переходы «сопоставление», «удаление» и «вставка» и устанавливая все вероятности переходов «совпадение-совпадение» на 1,0 (таким образом, нулевая стоимость), сама модель MSV уже устранила многие переходы, которые накапливают независимую ошибку округления, оставив в ядре моделируйте только вероятности эмиссии состояний совпадения (все они приблизительно независимы и некоррелированы в том, что касается анализа ошибок округления). Во-вторых, предполагается, что вероятности выбросов в состояниях N, C и J равны фоновым частотам (нулевая модель), поэтому оценки выбросов в состояниях N, C и J рассматриваются как нулевые по построению, поэтому они не вносят округления. Условия ошибки. В-третьих, мы можем воспользоваться тем фактом, что общий вклад переходов NN, CC и JJ приближается к константе для достаточно больших , потому что локальное выравнивание обычно относит почти все остатки целевой последовательности к состояниям N, C и J. и несколько, чтобы соответствовать государствам.Таким образом, мы ожидаем, что типичное локальное выравнивание будет включать переходы порядка NN, CC и JJ, каждый из которых оценивается , и биты для больших . Таким образом, мы можем оценить переходы NN, CC и JJ как нулевую стоимость во время рекурсии, а затем добавить постоянные биты обратно в оценку, чтобы аппроксимировать их недостающий вклад. Этот подход может изменить оптимальное локальное выравнивание (во время рекурсии пути, использующие переходы NN, CC и JJ, выглядят более благоприятными, чем они есть на самом деле), но в фильтре оценки нас интересует не оптимальное выравнивание, а только его оценка.

Таким образом, ошибка округления в реализации алгоритма MSV с пониженной точностью состоит из смещения, возникающего из-за обработки вкладов NN, CC, JJ, суммирующих биты, как константы -4,3 бита, и суммы более или менее независимых и равномерно распределенных членов ошибки, включая пять или более логарифмических вероятностей перехода () и оценки эмиссии для состояний совпадения, вовлеченных в неразрывные диагонали выравнивания остатков общей длины. Для больших , и предполагая или около того для типичных выравниваний MSV на границе статистической значимости, расчет обратной стороны конверта предполагает ожидаемую ошибку среднего нуля и стандартного отклонения около битов, а максимальную ошибку в худшем случае около битов.Поскольку выравнивания с более высокой оценкой включают в себя больше условий выделения совпадений, чем выравнивания с низкой оценкой, коррелируют с оптимальной оценкой, поэтому примерно гауссово распределение ошибок для заданного будет свернуто с распределением оценок Гумбеля, что приведет к слегка негауссовскому распределению ошибок. с некоторым перекосом в сторону большей ошибки.

Чтобы подтвердить, что эта ожидаемая ошибка округления согласуется с эмпирическими наблюдениями, я выполнил моделирование, в ходе которого я изучил различия в оценках MSV реализации с пониженной точностью (беззнаковые байты в битовых единицах) по сравнению с реализацией с плавающей запятой полной точности.Я сделал это для множества разных профилей (9 318 моделей из выпуска 22 Pfam), выровненных с 1000 случайных последовательностей различной длины и с 207 132 реальными последовательностями в SwissProt 49.0 (в UniProt 7.0). Этот эксперимент показал, что ошибки округления для каждой модели распределялись со стандартным отклонением 0,4–0,6 бита для реальных последовательностей в Swissprot и для случайных последовательностей каждой длины. Средняя ошибка была приблизительно равна нулю для случайных последовательностей длин ; занижение среднего значения на 0,4 бита для последовательностей UniProt; 0.5-битная средняя недооценка для случайных последовательностей; и 2,2-битная средняя недооценка для случайных последовательностей. На реальных последовательностях UniProt я наблюдал крайние различия вплоть до битов. Они неизменно соответствовали длинным и сильно смещенным последовательностям состава, где предположительно длина выравнивания была большой, что увеличивало вероятность накопленной ошибки округления. Поскольку они были редки, а MSV следует использовать только в качестве фильтра, эти крайности можно смело игнорировать. В целом диапазон ошибки округления кажется приемлемым, особенно для больших .

Показатели MSV подчиняются предположениям, что позволяет быстро определить P-значение

Ранее [31] я предположил, что ожидаемые оценки для некоторых вероятностных моделей локального выравнивания, включая модель локального выравнивания HMMER3, следуют легко предсказуемым распределениям. В частности, я предположил, что битовые оценки Витерби с оптимальным выравниванием показывают распределения Гумбеля с фиксированным наклоном, а хвост с высокими оценками битовых оценок прямого направления следует за экспонентами того же наклона. Модель MSV является полностью вероятностной и, следовательно, должна подчиняться этим предположениям.Следовательно, прогнозируется, что оптимальные оценки выравнивания MSV будут следовать распределению Гумбеля с наклоном и местоположением, которое оценивается путем подгонки к небольшому моделированию оценок из 200 или около того случайных последовательностей.

Этим статистическим предположениям лучше всего следуют модели или системы оценки с высокой относительной энтропией на позицию (т. е. с высоким средним ожидаемым результатом) [31]. Модели HMMER3 по умолчанию имеют низкую относительную энтропию на позицию (около 0,6 бит/позиция), потому что параметризация модели HMMER3 использует метод, называемый энтропийным взвешиванием [29], [37], специальный метод для повторного взвешивания эффективного числа наблюдаемых последовательности относительно предыдущей (псевдосчетчики) для достижения желаемой цели относительной энтропии.Стандартная система оценки парного выравнивания остатков (BLOSUM62) имеет аналогичную относительную энтропию, составляющую около 0,6 бит на выровненную позицию. При более низкой относительной энтропии на позицию для достижения высоких результатов требуются более длительные выравнивания, и «краевой эффект» конечной длины становится значительным. HMMER3 улучшает краевой эффект, вычисляя ad hoc скорректированных, где длина профиля в состояниях совпадения и относительная энтропия на состояние излучения совпадения в битах [31]. Хотя одна и та же специальная поправка достаточна для обоих распределений Витерби и Форвард, она была получена путем эмпирической подгонки с небольшим теоретическим руководством, поэтому мало оснований полагать, что такая же поправка применима к показателям MSV.Поэтому я эмпирически проверил способность оценивать точные P-значения для баллов MSV для широкого спектра моделей HMMER/Pfam.

На рис. 3А показан пример распределения баллов MSV для одного типичного профиля HMM (модель CNP1 из Pfam версии 24, представляющая семейство липопротеинов, выбранное потому, что оно имеет медианную длину, медианное число репрезентативных последовательностей и медианное среднее значение парной идентичности по все начальные выравнивания Pfam 24), для множества случайных iid последовательности разной длины. Для всех, кроме самых коротких последовательностей (L   =   25), наблюдаемые распределения оценок близко соответствуют предполагаемому распределению, включая случайных поправок на края членов (оранжевая линия).

Рис. 3. Оценки MSV имеют предсказуемое распределение.

A: пример распределения баллов MSV для типичной модели Pfam, CNP1, для случайного i.i.d. последовательности различной длины от 25 до 25 600, причем самая короткая, типичная и самая длинная длины выделены красной, черной и синей линиями соответственно.Прогнозируемое распределение, выполненное в соответствии с процедурой [31], включающей краевую коррекцию наклона, показано оранжевым цветом (хотя оно в значительной степени затемнено линиями данных прямо над ним). B: Гистограмма значений максимального правдоподобия, полученных из распределений оценок 11 912 моделей Pfam, показывающая, что большинство из них достаточно близко к предполагаемому, хотя и с большей дисперсией для моделей с энтропийно-взвешенными значениями по умолчанию (черная линия), чем для моделей с высокой относительной энтропией без энтропийно-взвешенных значений ( серая линия). C: наблюдаемая доля негомологичных последовательностей, которые проходят фильтр при значении P, равном 0.02 должно быть 0,02. Показаны гистограммы фактической доли фильтра для 11 912 различных моделей Pfam 24 для диапазона длин случайных последовательностей от 25 до 25 600 как для моделей по умолчанию (черные линии), так и для моделей с высокой относительной энтропией без энтропийного взвешивания (серые линии).

https://doi.org/10.1371/journal.pcbi.1002195.g003

На рисунке 3B показаны результаты моделирования, в которых 11 912 HMM различных профилей из Pfam версии 24 [11] были оценены алгоритмом MSV против случайных последовательностей длиной 400 , полученные распределения были приспособлены к распределениям Гамбеля для определения оценок максимального правдоподобия и , и построена гистограмма оценок.Для моделей с высокой относительной энтропией (серая линия) это распределение плотно сгруппировано на ожидаемом уровне. Для моделей, взвешенных по энтропии по умолчанию (черная линия), распределение шире с более высоким средним значением, в соответствии с тем, что наблюдается для оценок Витерби и объясняется краевым эффектом конечной длины.

На рис. 3C показана прямая оценка точности P-значений MSV для многих моделей Pfam и различных длин случайных последовательностей. Для каждой из 11 912 моделей Pfam 24 баллы MSV рассчитываются для 500 000 случайных последовательностей, сгенерированных для каждой из нескольких длин и , и подсчитывается количество случайных последовательностей, прошедших фильтр MSV в точке P.Если P-значения точны, мы ожидаем увидеть приблизительно нормальное распределение с центром в 2% случайных последовательностей, прошедших фильтр. В пределах допуска примерно двукратной ошибки это верно почти для всех моделей и для длины целевой последовательности или около того. Некоторые модели имеют менее предсказуемые распределения и дают небольшие выбросы. Наибольшие проблемы возникают с короткими целевыми последовательностями (), где P-значения могут быть примерно в пять раз завышены (т. е. проходит меньше последовательностей, чем предполагалось), как показано в примере CNP1 на панели A.Модели, взвешенные по энтропии по умолчанию (черные), подвержены большему влиянию, чем модели с высокой относительной энтропией (серые).

Этот анализ показывает, что в целом можно получить достаточно точные P-значения для баллов MSV. Это также показывает, что для коротких последовательностей или около того фильтр MSV может быть слишком агрессивным (удаление большего количества последовательностей, чем предполагалось), и что несколько моделей являются выбросами, поскольку через фильтр проходит либо слишком мало, либо слишком много последовательностей. Это незначительные проблемы, с которыми было бы неплохо разобраться в будущем.

Векторное распараллеливание алгоритмов Forward и Backward

Реализация MSV, описанная выше, примерно в 500 раз быстрее, чем стандартная последовательная реализация полного алгоритма Forward. Это означает, что скорость поиска по-прежнему будет ограничена скоростью вычислений вперед/назад, требующих значительных вычислительных ресурсов. Предположим, что мы позволяем 2% (1/50) верхних последовательностей пройти через фильтр MSV для полной прямой логарифмической оценки правдоподобия HMM; то Forward должен быть не более чем в 50 раз медленнее, чем MSV, иначе Forward будет ограничивать скорость. Поэтому необходимо было искать значительные ускорения хотя бы на порядок в реализациях алгоритмов Forward и Backward.

Числовая потеря значимости является проблемой для реализации алгоритмов прямого и обратного действия. Вероятность частичного выравнивания пути обычно ниже наименьшего представимого значения с плавающей запятой. В реализации Витерби недополнения можно избежать, работая в области логарифмической вероятности, заменяя умножение и максимизацию вероятностей сложением и максимизацией их логарифмов [5], [38].Однако рекурсии прямого и обратного динамического программирования требуют добавления частичных путей в вероятностной области.

Как в приложениях HMM для анализа последовательности, так и для распознавания речи эта проблема обычно решается путем работы в области логарифмической вероятности и реализации операции «логарифмическая сумма», так что сложение в области вероятности заменяется на , , и [5], [39]. Эффективная операция логарифмической суммы преобразует логарифмическую сумму в for и находит приблизительный термин для добавления в предварительно рассчитанную таблицу поиска, индексированную по разнице, масштабированной и округленной до соответствующей точности. Таблица поиска имеет конечный размер, потому что термин пренебрежимо мал для больших , но, тем не менее, он велик (16 000 записей в «общей» невекторизованной реализации HMMER3; см. logsum.c). Я не знаю, как эффективно реализовать большую таблицу поиска в векторных инструкциях SIMD. Только небольшие таблицы поиска кажутся возможными с использованием инструкций по перестановке векторов (возможно, до 256 записей в Altivec/VMX, меньше в SSE).

Другой подход — масштабирование [5], [38]. При изменении масштаба записи в каждой строке (для каждого целевого остатка) матрицы динамического программирования умножаются на некоторое значение масштаба.Значения масштаба выбираются таким образом, чтобы самые большие записи в каждой строке оставались в пределах допустимого числового диапазона. Если наименьшие значения в строке отличаются от наибольшего больше, чем числовой диапазон, наименьшие значения все еще теряют значение, но для многих HMM можно показать, что ни один префикс частичного пути, который не может быть переполнен, не мог когда-либо восстановиться, чтобы иметь незначительную вероятность как полный путь. Однако, как правило, это не относится к HMM профиля (и к другим HMM с путями, включающими состояния молчания) из-за возможности длинных удалений.Даже оптимальное выравнивание может содержать длинный путь D-D-D вдоль одной строки. После перемножения многих вероятностей перехода DD значения в состояниях в начале и в конце длинного пути удаления в одной и той же строке могут отличаться более чем на допустимый диапазон. Стандартный нормализованный 32-битный тип IEEE754 с плавающей запятой имеет диапазон около , что эквивалентно 256 битам в области оценки логарифмических шансов. Учитывая типичный штраф за расширение удаления примерно от -1 до -2 бит, удаление около 200 остатков или около того, как правило, будет занижать масштабированные состояния удаления на правильном пути.Делеции такой длины редки, но встречаются.

Я использую следующие шаги, чтобы сделать подход, который я называю «разреженным масштабированием», работающим для векторных реализаций SIMD HMMER3 алгоритмов Forward/Backward.

Во-первых, значения Forward/Backward рассчитываются в области отношения шансов, а не в области вероятности, поэтому они естественным образом предварительно масштабируются в некоторой степени. Вероятность выброса каждого совпадения заменяется его отношением шансов, тем же отношением, которое используется для оценок логарифмических шансов. По тем же аргументам, которые использовались для анализа недополнения реализации MSV выше, отношение шансов оптимального пути локального выравнивания в наихудшем случае является простой функцией длины модели и цели и с нижней границей около (около ), если мы принимаем как конструктивные ограничения, находящиеся в пределах допустимого диапазона представления с плавающей запятой IEEE754.

Во-вторых, я использую тот факт, что профиль HMMER3 HMM является моделью локального выравнивания с множественным попаданием, а не моделью глобального выравнивания (глобальный означает глобальный по отношению к модели, локальный по отношению к цели). Когда профиль HMM представляет собой модель локального выравнивания с несколькими попаданиями, работает подход масштабирования. Для любого пути с двумя выровненными областями, соединенными длинным удалением, должен существовать альтернативный путь, который считает те же две выровненные области двумя локальными выравниваниями, соединенными путем повторной инициации (MEJB).Этот путь повторной инициации только с тремя вероятностями перехода в одной и той же строке не представляет трудностей с потерей значимости. Путь с длинным удалением может быть потерян, но тогда его полный путь должен быть пренебрежимо мал по сравнению с альтернативным путем локального выравнивания с несколькими попаданиями.

Для определения подходящего коэффициента масштабирования необходимо проверить каждое значение в строке, что обычно требует дополнительных вычислений. Я использую тот факт, что значение в ячейке для состояния E уже вычислило максимум по всем состояниям.Достаточно использовать само значение ячейки E в качестве значения шкалы, установив значение ячейки E равным 1 и перемасштабировав все остальные значения в строке.

Тем не менее, масштабирование строки также требует дополнительных вычислений. Здесь я использую тот факт, что масштабирование каждой строки не требуется. Вместо этого, когда значение отношения шансов ячейки E превышает определенный порог, это запускает событие масштабирования для этой строки. В других рядах есть .

Я реализовал Forward и Backward, используя разреженное масштабирование и чередующиеся SIMD-векторы из четырех параллельных 32-битных чисел с плавающей запятой.В целом эти реализации примерно в 16 раз быстрее, чем стандартные последовательные реализации, использующие операцию таблицы поиска логарифмической суммы. Общее 16-кратное ускорение, вероятно, является комбинацией примерно 4-кратного ускорения от векторного распараллеливания SIMD и примерно 4-кратного от замены операции логарифмической суммы сложением и умножением. Это делает алгоритмы Forward/Backward примерно в 30 раз медленнее, чем фильтр MSV.

Конвейер ускорения HMMER3

Методы MSV и Forward/Backward, описанные выше, реализованы в так называемом «конвейере ускорения» в основе программной реализации HMMER3 (http://hmmer. janelia.org). Конвейер ускорения показан на рис. 4. Один вызов функции p7_Pipeline() выполняется для каждого сравнения модели/последовательности.

Рис. 4. Конвейер ускорения HMMER3.

Репрезентативные скорости вычислений показаны красным цветом в миллионах ячеек динамического программирования в секунду (Мк/с). Пороговые значения P по умолчанию для шагов фильтрации MSV, Витерби и прямой фильтрации показаны оранжевым цветом. Фильтр смещения и шаги определения домена подробно не описаны в этой рукописи и показаны серым цветом.

https://doi.org/10.1371/journal.pcbi.1002195.g004

Конвейер либо принимает, либо отклоняет все сравнение на каждом этапе на основе P-значения логарифмической оценки шансов. Например, по умолчанию фильтр MSV проходит, если сравнение получает P-значение менее 0,02 (т. е. ожидается, что 2% случайных негомологичных последовательностей с наивысшим баллом пройдут фильтр). Я еще не исследовал более сложный подход использования информации о выравнивании из более ранних и более быстрых шагов в конвейере для ограничения (полосы) последующих вычислений динамического программирования.

Все расчеты P-значения предполагают, что профиль запроса и целевая последовательность имеют состав остатков, близкий к общему среднему для белков. В некоторых случаях профиль запроса имеет предвзятую структуру, и эта предвзятость совпадает с предвзятостью, обнаруженной во многих последовательностях целевых баз данных. Мембранные белки, например, смещены в сторону более гидрофобного состава и имеют тенденцию соответствовать другим негомологичным мембранным белкам с более высокими баллами, чем ожидалось при простой нулевой гипотезе среднего состава.В HMMER3 есть методология пересчета баллов и P-значений для компенсации необъективной композиции, но эта методология (так называемая коррекция «null2», не описанная здесь из соображений экономии места) размещена в конце конвейера, поскольку требует больших вычислительных ресурсов. На этапе фильтра MSV нескорректированное значение P MSV может быть занижено при смещенных совпадениях состава, что означает, что больше ожидаемой доли негомологичных последовательностей может пройти через фильтр MSV, чего в некоторых случаях может быть достаточно для замедления конвейера. HMMER3 вставляет шаг «фильтр смещения», чтобы уменьшить эту проблему. Этап фильтра смещения показан серым цветом на рис. 4, поскольку он подробно не описан в данной статье. Вкратце, фильтр смещения вычисляет быструю, эвристически смещенную коррекцию состава для оценки фильтра MSV, используя скрытую марковскую модель с двумя состояниями, где одно распределение выбросов установлено для среднего состава белковых остатков, а другое распределение выбросов установлено для среднего состава запроса. профиль, полностью связанный четырьмя произвольными вероятностями перехода, настроенными вручную.Конвейер повторно оценивает последовательность с применением этой коррекции и повторно проверяет измененное значение P на соответствие пороговому значению фильтра MSV, равному 0,02. Фильтр смещения не влияет на итоговую оценку последовательности, которая рассчитывается с помощью полного алгоритма Forward; фильтр смещения имеет только эффект, заставляющий фильтр MSV удалять дополнительные совпадения, которые, по-видимому, связаны с предвзятой композицией.

Для дальнейшего снижения вычислительной нагрузки, возникающей на полном шаге Forward, в конвейер был реализован и вставлен дополнительный фильтр — фильтр Витерби.Фильтр Витерби представляет собой полосатую реализацию SIMD-вектора с оптимальным выравниванием с зазором по профилю (рис. 1А). Реализована 8-кратная векторная параллель в 16-битных целых числах, поскольку численный анализ накопления ошибки округления для Витерби менее благоприятен, чем для МСВ, и требуется большая точность. Следуя тем же аргументам, что и для MSV, оценки фильтра Витерби не занижаются (в расчетных пределах ), но могут переполнять 16-битное представление, которое находится в единицах 1/500 бит с целочисленным смещением 12 000, так что представляемые оценки диапазон от -89.от 5 до 41,5 бит. Любая оценка, превышающая верхний предел в 41,5 бита, в любом случае обязательно пройдет любое разумное P-значение фильтра (; пороговое значение фильтра Витерби по умолчанию равно ).

Алгоритмы Forward и Backward для конвейера реализованы в специализированных формах эффективной памяти, называемых p7_ForwardParser() и p7_BackwardParser(). Каждый синтаксический анализатор хранит только одну строку матрицы динамического программирования для каждого остатка последовательности, а также полные столбцы для «особых» состояний E, N, J, B и C.Это дает реализации с линейной памятью с достаточным количеством хранимой информации, чтобы обеспечить прямое/обратное апостериорное декодирование вероятных позиций состояний B и E в целевой последовательности, определяя вероятности конечных точек локального выравнивания. Целевая последовательность, которая проходит фильтр Витерби, оценивается с помощью полного алгоритма прямого синтаксического анализа. Если оценка Forward превышает порог P-значения (P по умолчанию), вычисляется анализатор Backward. Прямые/обратные вероятности используются для оценки локальных «областей» выравнивания со значительной апостериорной вероятностной массой в целевой последовательности.Затем каждая область подвергается концептуально отдельному конвейеру анализа, конвейеру «определения домена», который идентифицирует отдельные гомологичные области и выравнивания с использованием ряда шагов, включая полноматричное прямое/обратное выравнивание, апостериорное декодирование, выравнивание с максимальной ожидаемой точностью и коррекция предвзятой оценки состава для конкретного региона. Процедура определения домена подробно не описывается в этой статье.

Конвейер ускорения эффективно использует память. Фильтры MSV и Viterbi занимаются только оценками, а не выравниваниями, поэтому они реализованы в формах с линейной памятью, которые хранят только одну строку динамического программирования.Алгоритмы Forward и Backward используются в только что описанной форме «парсера». Однако конвейер определения домена неэффективно использует память. В настоящее время он вычисляет полные матрицы прямого/обратного и апостериорного декодирования для каждой идентифицированной подпоследовательности (области) длины в целевой последовательности. Пока эти шаги в постпроцессоре предметной области не будут заменены более эффективными алгоритмами памяти, HMMER3 может иногда исчерпать доступную память для некоторых больших сравнений моделей/последовательностей.

Тест скорости

На рис. 5 показаны эталонные измерения скорости HMMER3 по сравнению со скоростью BLAST [3], FASTA [40], SSEARCH (реализация FASTA Smith/Waterman), HMMER2 и программного обеспечения UCSC SAM profile HMM [37]. .Скорость поиска указана в миллионах ячеек динамического программирования в расчете на секунду (Мк/с), измеренных на одном ядре процессора (см. Методы). Количество ячеек динамического программирования является произведением длины запроса и длины целевой базы данных в остатках. Простая реализация выравнивания последовательности динамического программирования масштабируется во времени как , поэтому ожидается, что отчет о скорости в единицах Mc/s будет относительно независимым от длины запроса и цели. На практике самые быстрые программы поиска, как правило, демонстрируют некоторую дополнительную зависимость от длины последовательности запросов, при этом более эффективная работа выполняется при более длинных запросах.На рис. 5 представлен ряд различных запросов разной длины.

Рисунок 5. Тесты скорости.

Каждая точка представляет собой измерение скорости для одного поиска с одним запросом к целевым последовательностям (для медленных программ HMMER2 и SAM, для FASTA и SSEARCH) на одном ядре ЦП (подробнее см. Методы). Обе оси являются логарифмическими, для скорости в миллионах ячеек динамического программирования в секунду (Мк/с) по оси y и длины запроса в остатках по оси x. На панели A показаны измерения скорости «типичная наилучшая производительность» для нескольких различных программ, включая HMMER3, для 76 запросов различной длины консенсуса, выбранных из Pfam 24, для поиска рандомизированных (перетасованных) целевых последовательностей.На панели B показан более широкий диапазон более реалистичных измерений скорости для всех 11 912 профилей в Pfam 24 при поиске реальных последовательностей целевых белков из UniProt TrEMBL.

https://doi.org/10.1371/journal.pcbi.1002195.g005

Чтобы измерить «типичную» производительность каждой программы, не усложняя вариации, возникающие в результате получения объемных результатов выравнивания для некоторых запросов, которые затрагивают большие суперсемейства белков, панель A (слева) показывает эталонные тесты, выполненные на случайных (перемешанных) целевых последовательностях.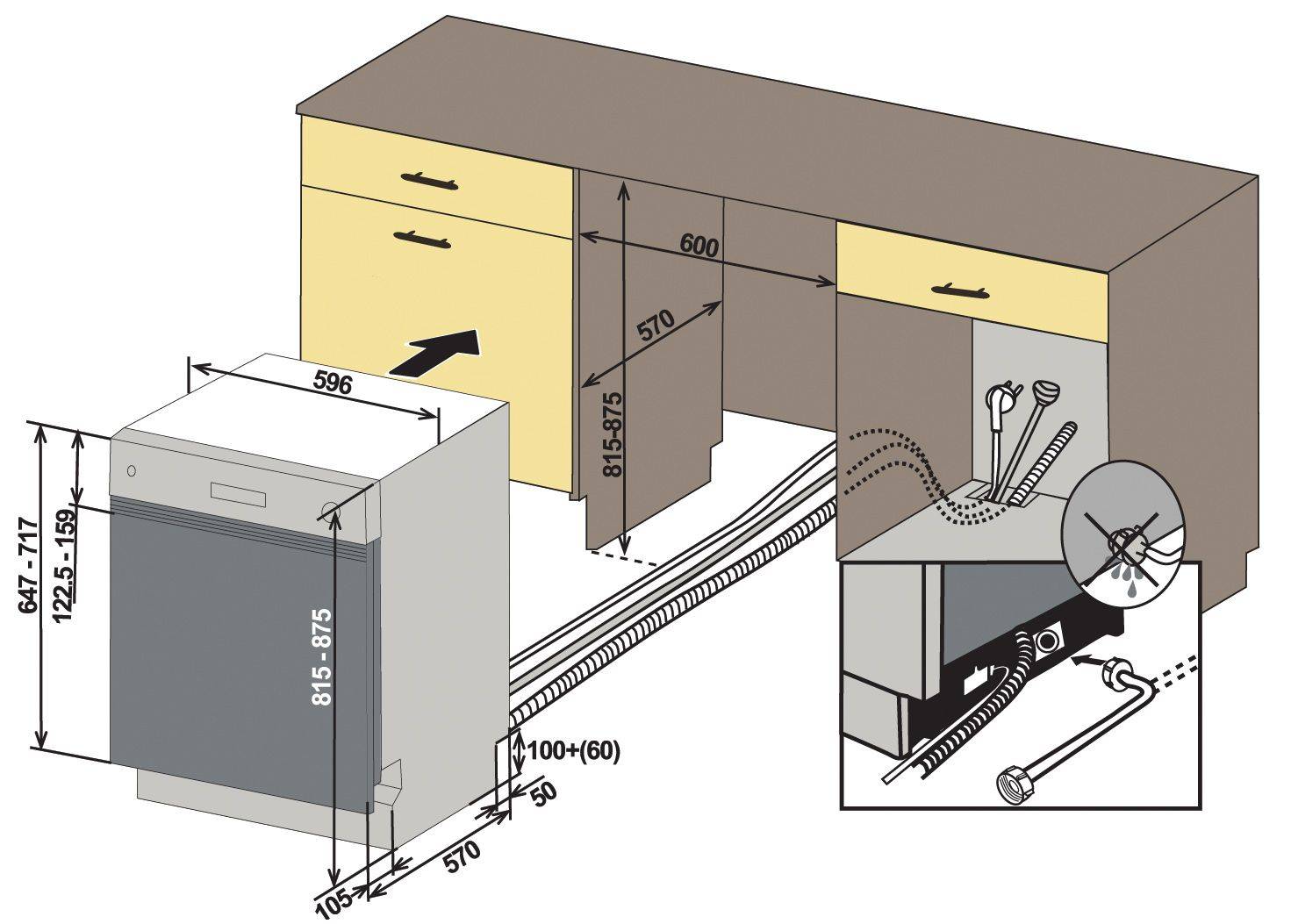 Панель показывает результаты для 76 профилей запросов (или репрезентативных одиночных последовательностей), выбранных для выборки полного диапазона длин запросов в базе данных белковых доменов Pfam от 7 до 2217 остатков. Эти результаты показывают, что производительность HMMER3 сравнима с другими быстрыми программами поиска в базе данных; несколько медленнее (примерно в 2–3 раза), чем NCBI BLAST, и несколько быстрее (примерно в 3 раза), чем, например, WU-BLAST. На этом рисунке стоит отметить скорость SSEARCH, реализации локального выравнивания Smith/Waterman в пакете FASTA; Недавно программа SSEARCH была ускорена за счет внедрения полосатых векторных методов SIMD Фаррара, что позволило достичь скорости, сравнимой с эвристическими программами FASTA и WU-BLAST.HMMER3 быстрее, чем HMMER2, до 140 раз, хотя HMMER3 вычисляет полные оценки вперед, тогда как HMMER2 вычисляет более быстрые оценки оптимального выравнивания Витерби. По сравнению с SAM, который вычисляет полные оценки Forward, HMMER3 примерно в 600 раз быстрее.

Для измерения более широкого и более реалистичного диапазона реальной производительности на панели B (справа) показаны эталонные показатели для 11 912 различных запросов (каждый профиль Pfam 24) на реальных последовательностях из UniProt Trembl. Программы, которые просто выполняют динамическое программирование выравнивания для каждой целевой последовательности, такие как HMMER2 (оранжевые точки) или SSEARCH (не показаны), демонстрируют производительность, практически независимую от свойств запроса и целевых последовательностей.Однако программы, использующие эвристику и фильтры, чувствительны к тому, насколько хорошо данный поиск подчиняется предположениям пороговых значений эвристики и/или фильтра. Скорость как HMMER3, так и PSI-BLAST зависит не только от длины запроса, но также существенно зависит от их среднего значения для заданной длины запроса. Скорость PSI-BLAST на панели B варьируется как вверх (примерно в 3 раза), так и вниз (примерно в 10 раз) по сравнению с его «типичными» характеристиками на панели A, предположительно отражая различия в количестве попаданий слов и совпадений. расширения должны быть обработаны для данного поиска.Скорость HMMER3 имеет тенденцию изменяться только в меньшую сторону по сравнению с ее типичной производительностью, примерно в 20 раз. На панели B я выделяю примеры четырех самых неэффективных поисков HMMER3 на моделях DivIC, DUF972, IncA и MFS_1. Даже если этап фильтра смещения включен в конвейер ускорения, основной причиной более низкой производительности поиска HMMER3 остаются смещенные последовательности композиции (например, трансмембранные белки), в которых большее количество сравнений проходит через быстрые фильтры конвейера ускорения, чем ожидалось по расчетам P-значения, которые предполагают средние составы целевой последовательности, что приводит к большему количеству сравнений для достижения ресурсоемких расчетов вперед/назад.

Сравнительный анализ чувствительности/специфичности

Подход с фильтрацией, как правило, в некоторой степени снижает чувствительность поиска, поскольку фильтр с определенной скоростью ошибочно удаляет истинные гомологи. Мы хотим, чтобы эта скорость была незначительной. Чтобы измерить, насколько снижается чувствительность поиска при использовании фильтра MSV и конвейера ускорения HMMER3, я выполнил тесты для сравнения чувствительности/специфичности стандартного HMMER3 hmmsearch (с конвейером фильтра ускорения) с параметром hmmsearch —max, который превращает отключает все фильтры и запускает полный алгоритм прямой оценки для каждой целевой последовательности.Я также протестировал HMMER2 и несколько других программ поиска гомологии для сравнения. Эти результаты показаны на рисунке 6.

Рисунок 6. Сравнительный анализ чувствительности и специфичности поиска.

Для разных программ поиск осуществляется либо путем построения единого профиля из выравнивания запросов (HMMER3, HMMER2, SAM, PSI-BLAST), либо с помощью «семейного попарного поиска» [41], в котором каждая отдельная последовательность используется как запрос и лучшее значение E для целевой последовательности записывается (BLASTP, SSEARCH, FASTA). В каждом эталонном тесте были выбраны истинно положительные подпоследовательности, которые не более чем на 25% идентичны любой последовательности в выравнивании запроса (см. Методы). На панели А показаны результаты, в которых негомологическая последовательность была синтезирована с помощью простой случайной модели, и каждая истинно положительная последовательность содержит одну встроенную гомологичную подпоследовательность (всего 2141 запрос множественных выравниваний, 11 547 истинно положительных последовательностей и 200 000 ловушек). На панели B показаны результаты, в которых негомологическая последовательность синтезирована путем перетасовки случайно выбранных подпоследовательностей из UniProt, и каждый истинно положительный результат содержит две встроенные гомологичные подпоследовательности (всего 2141 выравнивание по запросу, 24040 истинно положительных последовательностей и 200000 ложных последовательностей).Ось Y представляет собой долю истинных срабатываний, обнаруженных со значением E лучше, чем количество ложных срабатываний на запрос, указанное на оси X.

https://doi.org/10.1371/journal.pcbi.1002195.g006

Эти тесты автоматически и полуслучайно генерируются программой (create-profmark). Программа начинается с источника надежных выравниваний гомологичных белковых доменов (здесь выравнивания семян Pfam 24), источника типичных полноразмерных белковых последовательностей (здесь UniProt SwissProt 2011_03) и выбора метода синтеза негомологичных сегментов последовательностей ( например, перемешивание случайно выбранного сегмента последовательности UniProt).Выравнивание запроса и набор истинных тестовых доменов (доверено, что они гомологичны запросу) создаются путем применения кластеризации с одинарной связью по процентной идентичности к выравниванию Pfam и использования этой кластеризации для выбора последовательностей, таких, что ни один истинный тестовый домен не имеет попарная идентичность более чем на 25% для любой последовательности в выравнивании запроса и не более чем на 50% попарная идентичность для любого другого тестового домена. Настоящие тестовые последовательности создаются путем объединения одного или двух тестовых доменов вместе с негомологичными сегментами последовательности, при этом общая длина последовательности выбирается из распределения последовательностей UniProt.Ложные (негомологичные) тестовые последовательности создаются путем конкатенации негомологичных сегментов последовательности, при этом как длина сегмента, так и общая длина последовательности выбираются из распределений длин истинных тестовых последовательностей. Процедура, ее обоснование и некоторые предостережения более подробно описаны в Методах.

Для сравнительного анализа метода профиля (HMMER, SAM или PSI-BLAST) профиль создается на основе каждого выравнивания запроса и выполняется поиск в целевой базе данных тестовых последовательностей и ложных целей. Результаты всех поисков (для всех разных запросов) объединяются и сортируются по E-значению, и этот ранжированный список используется для расчета доли истинных срабатываний, обнаруженных при увеличении порогов ложных срабатываний на запрос от 0. от 001 до 10.

Для более справедливого сравнения метода запроса с одной последовательностью (BLAST, SSEARCH, FASTA) с методами профиля используется метод семейного парного поиска (FPS) [41] (в отличие от выбора только одной последовательности запроса из выравнивания). . Каждая отдельная последовательность в выравнивании запроса ищется в целевой базе данных; лучшее E-значение, найденное для любой последовательности запроса, рассматривается как E-значение целевой последовательности, а результаты для всех запросов объединяются, сортируются и обрабатываются, как указано выше.

На рис. 6 показаны результаты двух разных эталонных тестов. На панели А показаны результаты, в которых истинные тестовые последовательности имеют один встроенный домен, а негомологичные последовательности синтезированы как i.i.d. (независимая одинаково распределенная) случайная последовательность из среднего частотного распределения остатков UniProt; имеется 2141 сопоставление запросов, 11 547 истинных тестовых последовательностей и 200 000 ложных целей. Поскольку негомологичные последовательности нереально просты (нет смещенной композиции, нет повторяющейся последовательности), этот эталонный тест не использует различные поправки на смещенную композицию, которые есть в некоторых программах (таких как HMMER и BLAST), и является скорее базовым тестом наилучшего. чувствительность программы поиска к регистру.На панели B показаны результаты моего теста profmark по умолчанию, в котором есть два встроенных домена на настоящую тестовую последовательность (чтобы проверить способность программы правильно обнаруживать и выравнивать несколько доменов на последовательность, хотя такие результаты здесь не показаны), и где сегменты негомологичной последовательности создаются путем перетасовки случайно выбранных сегментов последовательностей UniProt. Поскольку негомологичные сегменты в этом эталонном тесте могут показывать более реалистичные смещения состава моноостатка (но не смещения более высокого порядка, такие как тандемные повторы), эта версия эталонного теста является более реалистичной и использует больше специальных частей программ, которые пытаются скорректировать систематическую ошибку. сочинение.На панели А показаны результаты, которые в значительной степени не зависят от предвзятости композиции, но менее реалистичны. На панели B показаны результаты, которые в большей степени зависят от способности программы обрабатывать предвзятую композицию и, вероятно, более реалистичны.

Основной результат на обеих панелях заключается в том, что чувствительность и специфичность практически идентичны для HMMER3 как с конвейером ускорения (темные черные линии), так и без него (—max; красные линии). Существует небольшая потеря чувствительности, вызванная конвейером ускорения, но эта потеря более чем компенсируется усилением чувствительности HMMER3 по сравнению с HMMER2 (либо в режиме «глобального» поиска выравнивания по умолчанию, либо в режиме поиска локального выравнивания; оранжевые кружки и квадраты соответственно).При высокой специфичности (низкий уровень ложных срабатываний) на более реалистичных смещенных приманках HMMER3 по умолчанию может оказаться лучше, чем нефильтрованный HMMER3 (hmmsearch —max), потому что фильтр смещения удаляет некоторые проблемные смещенные ложноположительные ложные ложные срабатывания, которые предположительно более мощные смещенные исправления состава в HMMER3 Forward оценки не исправляются.

Тесты для других программ (таких как BLAST, SAM, FASTA и SSEARCH) показаны только для приблизительного сравнения. Цель состоит не в том, чтобы тщательно сравнить HMMER с этими программами, а в том, чтобы дать дополнительное ощущение масштаба, поместив разницу между HMMER3 с конвейером ускорения и без него в контексте, то есть показав, что разница между HMMER3 с конвейером ускорения и без него незначителен по сравнению с различиями между программами.Эти программы запускались только в конфигурации по умолчанию. Я не исследовал доступные варианты, которые могли бы улучшить их производительность в этом тесте. Хотя я считаю результаты справедливыми и репрезентативными, я должен интерпретировать их с осторожностью. Я регулярно тестирую HMMER на этих тестах во время разработки. Невозможно избежать некоторого обучения тесту, даже несмотря на то, что тесты несколько рандомизированы. Тем не менее, некоторые информативные тенденции в этих результатах согласуются с предыдущими независимыми опубликованными бенчмарками других групп, поэтому сравнения, вероятно, полезны в качестве приблизительного ориентира. Например, Мадера и Гоф опубликовали бенчмарк [28], в котором они пришли к выводу, что SAM значительно превосходит HMMER2, что в то время не согласовывалось с моим опытом. Джонсон [29] проследил это до того, что Мадера и Гоф переключили HMMER2 с режима глобального выравнивания по умолчанию на режим локального поиска не по умолчанию, который мы не тратили много времени на тестирование или настройку, и мы ранее не понимали, насколько чувствительно локальное выравнивание относится к информативности модели на позицию. Это привело нас к пониманию того, насколько важен метод энтропийного взвешивания SAM для локального выравнивания, в то время как он гораздо менее важен для глобального выравнивания [29].Эта история отражена в тестах на рисунке 6, где локальное выравнивание HMMER2 работает плохо по сравнению с SAM, выравнивание HMMER2 glocal сравнимо с SAM, а локальное выравнивание HMMER3 (с методом энтропийного взвешивания), возможно, немного лучше. чем САМ. Большая часть различий между HMMER3 и SAM заключается в режиме высокой специфичности более реалистичного эталона, который включает сегменты предвзятого состава (панель B), и, таким образом, вероятно, является результатом различий в корректировках состава смещения ad hoc , которые различаются. между SAM и HMMER, а не какие-либо принципиальные различия в параметризации их профилей HMM или их алгоритмах оценки вперед, которые, как я считаю, очень похожи.

Другая история, отраженная в этих тестах, связана с широко распространенным мнением о том, что полное выравнивание Смита/Уотермана превосходит быстрое эвристическое приближение Смита/Уотермана BLAST. Это верно в более простом тесте (панель A), но не в том случае, когда последовательности-приманки включают в себя необъективные сегменты композиции (панель B). Действительно, на панели A все три программы быстрого поиска последовательностей (WU-BLAST, NCBI-BLAST и FASTA) работают примерно одинаково (и хуже, чем SSEARCH), тогда как на панели B NCBI BLAST превосходит WU-BLAST, FASTA и SSEARCH.Это снова, вероятно, показывает важность необъективных поправок на оценку композиции. Смещенная коррекция состава привлекла пристальное внимание при разработке программного обеспечения NCBI BLAST [7], [8], [42], но не является частью учебника, описывающего «оптимальное» локальное выравнивание Смита/Уотермана.

Мой главный вывод (о том, что конвейер ускорения оказывает незначительное влияние на чувствительность/специфичность HMMER3 по сравнению с неускоренной опережающей оценкой) подтверждается более прямым экспериментом.Я провел поиск по всем 11 912 HMM профиля Pfam 24 по сравнению с 516 081 последовательностями в UniProt SwissProt 2011_03, используя пять различных настроек параметров hmmsearch, начиная с —max и затем последовательно включая один шаг фильтра за раз в конвейере ускорения (MSV, смещение, Витерби). и вперед), вплоть до конфигурации по умолчанию со всеми четырьмя этапами фильтра. С помощью —max было найдено в общей сложности 799 893 совпадения с E-значением 0,0001 или меньше. При включении фильтра MSV теряется 718 обращений (0,09%). В целом конвейер по умолчанию со всеми этапами фильтрации теряет 2701 обращение (0.3%). Различия в значительных совпадениях не обязательно все связаны с истинными гомологами. Нефильтрованный поиск может найти ложное срабатывание, которое будет удалено одним или несколькими фильтрами. Однако большинство этих различий, по-видимому, являются истинными гомологами, которые удаляются фильтрами. Помимо 718 совпадений, удаленных фильтром MSV, подавляющее большинство других потерь происходит из-за того, что фильтр смещения ненадлежащим образом удаляет последовательности, которые имеют сильно смещенные композиции, но также содержат область истинной гомологии.Наиболее очевидные проблемы с чувствительностью/специфичностью HMMER3, по-видимому, связаны с его фильтром смещения и коррекцией оценки состава смещения, а не с использованием фильтра MSV в качестве основного ускорения.

Обсуждение

Описывая эвристику MSV и другие методы ускорения, реализованные в HMMER3, я не рассматривал вопрос о том, лучше или хуже эвристика MSV, чем другие эвристики, например, в BLAST или FASTA. В тестах чувствительности/специфичности (рис. 6) BLAST и FASTA работают примерно так же, как неускоренный Smith/Waterman, а HMMER3 работает примерно так же с конвейером ускорения и без него. Это показывает, что общая чувствительность и специфичность этих программ ограничены не их соответствующими эвристиками, а скорее их фундаментальными (неускоренными) методами сравнения последовательностей. Таким образом, лучшая эвристика вряд ли улучшит общую чувствительность/специфичность. Лучшей эвристикой будет более быстрая с той же чувствительностью/специфичностью. В вопросе о скорости мы не можем удовлетворительно показать, что один алгоритм обязательно быстрее другого. Мы можем только строго сравнивать конкретные реализации.Попытка смешивать и сопоставлять различные эвристические подходы и проводить окончательное сравнение их полностью оптимизированных скоростей требует трудоемких усилий по проектированию и оптимизации, посвященных каждой реализации. Таким образом, остается открытым вопрос, можно ли, например, настроить эвристику в стиле BLAST, чтобы иметь достаточную чувствительность / специфичность, чтобы соответствовать производительности HMMER3, но при этом оставаться быстрее. Я разработал MSV, потому что это было легко для меня, а не потому, что я попробовал разные эвристики и обнаружил, что MSV лучше.Я работал над чередующейся SIMD-векторизацией алгоритма Витерби, и реализация MSV легко получается из полосатой SIMD-Витерби, просто удаляя код, который обрабатывает удаления и вставки. Эвристические подходы в BLAST и FASTA имеют то преимущество, что последующие более медленные вычисления сосредоточены на определенных диагоналях, тогда как в текущем подходе HMMER мы расточительно пересчитываем полные выравнивания последовательностей на каждом этапе конвейера ускорения. Я ожидаю, что будет полезно разработать эвристики, ориентированные на диагонали с высокой вероятностью, как это делают BLAST и FASTA, используя методы векторизации SIMD HMMER.

Хотя эта статья посвящена методам ускорения, используемым в HMMER3, HMMER3 также кажется более чувствительным, чем HMMER2. Основной причиной этого является принятие «энтропийного взвешивания», метода, представленного группой Калифорнийского университета в Санта-Круз в пакете SAM profile HMM [29], [37], где информационное содержание каждой позиции сводится к заданной цели. количество бит. Второй причиной является переход от оценок оптимального выравнивания по Витерби к показателям Forward, суммированным по ансамблю выравнивания [29].

С другой стороны, я считаю, что переход от глобального выравнивания по умолчанию в HMMER2 к локальному выравниванию в HMMER3, вероятно, поставил под угрозу некоторую чувствительность поиска («глобальный» означает глобальный в запросе, локальный в целевой последовательности: требуется домен полной длины выравнивание). Восстановление глобального выравнивания по HMMER3 должно улучшить производительность поиска для профилей, которые, как ожидается, будут совпадать по всей своей длине, таких как модели белковых доменов Pfam. Однако быстрая статистика E-значения для оценок прямого и обратного направлений (включая оценки фильтра MSV) действительна только для локального выравнивания, а числовой анализ потери значимости метода разреженного масштабирования в реализации прямого/обратного направления предполагает локальное выравнивание. Обе проблемы должны быть решены, прежде чем глобальное выравнивание будет полезно реализовано в HMMER3.

Здесь я описал только одноядерную производительность. Я не обсуждал распараллеливание между несколькими ядрами. Поисковые программы HMMER3 включают рудиментарные реализации потоков POSIX и распараллеливания MPI (передача сообщений в кластере вычислительных узлов). Эти реализации в настоящее время плохо масштабируются, до скромного количества процессорных ядер (например, от 2 до 4 для многопоточности).Улучшенное распараллеливание является приоритетом для будущих разработок.

Обработка смещенных последовательностей композиций в HMMER3 проблематична. Я решил ввести специальный «фильтр смещения» в конвейер ускорения, чтобы иметь дело с небольшим количеством профилей, которые пропускают слишком много последовательностей через фильтр MSV и вязнут на медленных этапах вперед/назад конвейера. Фильтр смещения иногда отфильтровывает истинно положительные совпадения. Возмущающий режим отказа может возникнуть, когда целевая последовательность состоит из гомологичной подпоследовательности, окруженной большим количеством негомологичной последовательности со смещенным составом; в этом случае фильтр смещения может агрессивно удалить всю последовательность.Хотя другие программы поиска в базе данных имеют аналогичные проблемы с чрезмерно агрессивной маскировкой состава, одним из будущих направлений разработки HMMER3 будет улучшение его формальной вероятностной модели гомологичной последовательности , не относящейся к .

В этом документе описывается начальный базовый уровень производительности HMMER3 на одном ядре процессора. Перспективы существенных улучшений в будущем хорошие. Есть много очевидных возможностей для поэтапной оптимизации. Бьерн Кнудсен (CLCbio, Орхус, Дания) уже внес важный вклад в оптимизацию фильтра MSV, который увеличивает общую скорость HMMER3 примерно в два раза.Оптимизация Кнудсена появится в следующем выпуске кода HMMER, и мы, вероятно, опишем ее в следующей рукописи. Другой возможностью оптимизации является предварительная обработка файла последовательности целевой базы данных в эффективный двоичный формат, как это делает BLAST со своими базами данных BLAST. HMMER3 по-прежнему читает стандартные базы данных последовательностей плоских файлов, такие как текстовые форматы FASTA и UniProt. Другая возможность оптимизации состоит в том, чтобы преобразовать фильтры в конвейере из их текущего режима фильтрации целых целевых последовательностей (что было легко реализовать) для хранения и извлечения дополнительной информации о местонахождении массы вероятности выравнивания, поэтому последующие шаги (включая прямое/обратное ) можно выполнять как расчеты динамического программирования с диапазонами внутри высоковероятностных конвертов, в отличие от повторной обработки всего сравнения запроса и цели на каждом этапе конвейера.Благодаря этим и другим простым возможностям оптимизации я ожидаю, что скорость HMMER3 превзойдет скорость NCBI BLAST в относительно ближайшем будущем.

Эта скорость позволяет применять технологию профильного HMM к стандартному поиску в базе данных последовательностей с помощью запросов с одной последовательностью, включая итеративный поиск в базе данных. Независимая от позиции система подсчета очков для одиночных последовательностей является лишь частным случаем профилированной системы подсчета очков, зависящей от позиции. «Профиль» HMM может быть построен из одной последовательности с использованием независимых от позиции вероятностей, полученных из стандартных оценочных матриц, таких как BLOSUM62, плюс пара параметров для вероятностей открытия и расширения разрыва.Программный пакет HMMER3 включает программу phmmer для поиска в базе данных белков, аналогичную blastp , и программу jackhmmer для итеративного поиска в базе данных белков, аналогичную psiblast . Эти программы, их параметризация и эффект расширения технологии HMM профиля, алгоритма Forward и методов вероятностного вывода для рутинного поиска в базе данных последовательностей будут описаны в другом месте.

Самая интересная книга о памяти, которую вы когда-либо читали, Дайан Суонсон