Способ измерения сопротивления заземления: Обзор методов измерения сопротивления заземления
Заземление используется в реализации различных проектов электрических систем. Само понятие “заземление” схематично рассматривается подключением участка электрической цепи к потенциалу земли.
Контур заземления содержит проводник и электрод, внедрённый глубоко в грунт. Традиционным действием в электротехнической практике является измерение сопротивления заземления только ещё запускаемых и уже эксплуатируемых сетей. Мы расскажем, как и каким образом производится это важное действие.
Содержание статьи:
Для чего необходимы измерения?
Блестящее решение перечисленных ниже задач достигается идеальным нулевым сопротивлением в заземляющей цепи:
- Не допустить появления напряжения на корпусе технологических машин.
- Добиться эффективного опорного потенциала электроаппаратуры.
- Полностью устранить статические токи.
Правда электротехнический опыт показывает: результат под идеальный нуль получить невозможно.


Процедура исполнения необходимых замеров с помощью прибора для определения сопротивления заземляющей шины. Такие процедуры проводятся по графику, который утверждается руководством обслуживающей организации
В любом случае, заземлённый электрод выдаёт какое-никакое сопротивление.
Конкретную величину resistance определяют:
- сопротивление электрода в точке контакта с проводящей шиной;
- контактная область между земляным электродом и грунтом;
- структура грунта, дающая разное сопротивление.
Практика измерений сопротивления контура заземления отмечает, что первыми двумя факторами вполне можно пренебречь, но при соблюдении логичных условий:
- Заземляющий электрод сделан из металла с высокой электропроводимостью.
- Тело штыря электрода тщательно зачищено и плотно посажено в грунт.
Остаётся фактор третий – резистивная поверхность грунта. Он видится главной расчётной деталью для измерений сопротивления контура заземления.
Вычисляется же благодаря формуле:
R = pL / A,
где: p – удельное сопротивление грунта, L – условное заглубление, А – рабочая площадь.
Чтобы обезопасить владельцев дома/квартиры, заземлением должны быть снабжены все виды мощного домашнего электрооборудования:
Галерея изображений
Фото из
Все виды бытового энергозависимого оборудования, эксплуатируемого в квартирах и домах, необходимо подключать к автономным или общественным системам заземления
Для подключения электроприборов к заземляющей системе необходимо устанавливать розетки с заземляющими контактами, снабженными либо выходящими за пределы корпуса медными скобами, либо третьим отверстием, предназначенным для погружения контакта штепселя с тремя штырями
Обязательному заземлению подлежат все виды холодильного оборудования (холодильники, морозильные шкафы, МВП, электроплиты, стиральные машины
Подключение к заземляющему контуру обязано производится согласно схеме, приложенной производителем технической продукции, с использованием рекомендованных им средств
Обязательно необходимо выполнить заземление гидромассажной ванны, т.к. в ее работе используются электроприборы
В беспрекословном заземлении нуждаются все виды сетевых машин, начиная от домашнего стационарного компьютера до серверных шкафов, в том числе электрошкафы для автоматов и УЗО
Необходимо заземлять все модели энергозависимых газовых котлов: как напольные, так и настенные
Все линии заземления прокладывают по параллельной схеме, последовательное подключение к заземляющей системе недопустимо
Варианты заземляющих контактов
Штепсельная розетка с заземляющим контактом
Заземление кухонной бытовой техники
Подключение стиралки к заземляющему контуру
Устройство заземления гидромассажной ванны
Способ заземления сетевого оборудования
Заземление напольного газового котла
Подключение линий заземления к шине
При тестировании сопротивления каждую из заземляющих линий проверяют отдельно. Сопротивление между заземляющим элементом и каждой не проводящей ток частью электрооборудования, попадание под напряжение которой возможно, должно быть меньше 0,1 Ом.
Обзор измерительных способов
Существует несколько вариантов измерения сопротивления , каждый из которых вполне точно позволяет определить искомую величину.
3-точечная система определения
Так, например, часто применяется методика 3-х точечной схемы, основанная на эффекте падения потенциала.
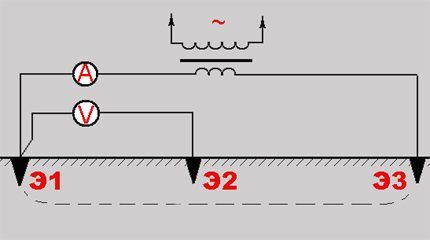

Графическая схема так называемой трёхточечной системы, которую достаточно часто применяют, когда требуется измерить значение сопротивления заземляющего контура
Измерения выполняют за три основных шага:
- Замер напряжения на электроде Э1 и зонде Э2.
- Замер силы тока на электроде Э1 и зонде Э3.
- Расчёт (формулой R = E / I) сопротивления заземляющего электрода.
Для этой методики точность замеров логически зависима от места инсталляции зонда Э3. Его рекомендуется внедрять в грунт на удалении – оптимально за пределы так называемой области ЭСЭ (эффективного сопротивления электродов) Э1 и Э2.
Измерения по технологии «62%»
Если структура грунта под размещение заземляющего электрода отличается однородным содержимым, методика «62%» для определения сопротивлений контуров заземления обещает хорошую результативность.
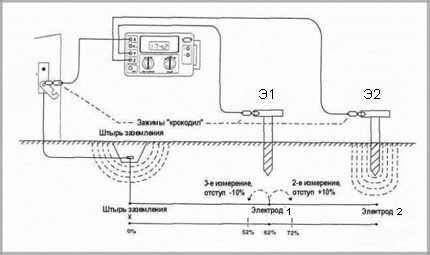

Схема под технологию измерений под интересным названием «62%». Однако название взято от оптимальной величины отступа между электродами, при которой получают приемлемый результат
Способ применим под схемы с единственным заземляющим электродом. Точность показаний здесь обусловлена возможностью расположения рабочих зондов на прямолинейном участке, относительно заземляющего электрода.
Точки инсталляции контрольных зондов
| Заглубление электрода, м | Расстояние до зонда Э1, м | Расстояние до зонда Э2, м |
| 1,8 | 13,7 | 21,9 |
| 2,4 | 15,25 | 24,4 |
| 3,0 | 16,75 | 26,8 |
| 3,6 | 18,3 | 29,25 |
| 5,5 | 21,6 | 35,0 |
| 6,0 | 22,5 | 36,6 |
| 9,0 | 26,2 | 42,65 |
Упрощённый двухточечный метод
Применение этого способа измерений требует наличия ещё одного качественного заземления помимо того, которое будет подвергаться исследованию. Методика актуальна для территорий густонаселённых, где часто нет возможности широко оперировать вспомогательными рабочими электродами.
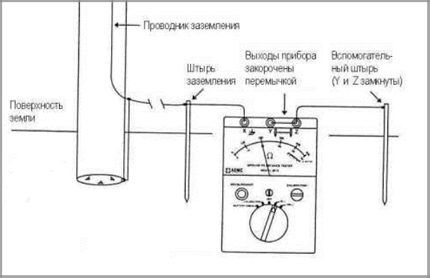

Упрощённая методика измерений производится по двухточечной схеме. При такой технологии требуется меньше манипуляций с оборудованием и расчётами, но точность расчетов невысока
Метод двухточечного измерения отличается тем, что одновременно показывает результат для двух устройств заземления, включенных последовательно. Этим и объясняются требования к высокому качеству исполнения второго заземления, чтобы не учитывать его сопротивление.
Для выполнения вычислений также измеряется сопротивление заземляющей шины. Полученный результат вычитывают из результатов общих замеров.
Точность этого способа оставляет желать лучшего по сравнению с двумя вышеизложенными. Здесь существенную роль играет расстояние между заземляющим электродом, сопротивление которого измеряется и вторым заземлением. Стандартно такая методика не применяется. Это своего рода альтернатива, когда нельзя использовать другие способы измерений.
Точные измерения по четырём точкам
Для большинства вариантов измерения сопротивлений наиболее оптимальным способом, помимо 2-х и 3-х точечных, считается 4-х точечная технология. Такой технологией замеров наделены приборы, подобные тестеру 4500 серии. Судя из наименования метода, на рабочей площадке в одну линию и на равных расстояниях размещаются четыре рабочих электрода.


По такой схеме – четырехточечной, производятся самые точные измерения. Используется современная аппаратура и есть возможность выполнять работы без отключения заземляющей цепи
Генератор тока прибора подключается на крайние электроды, в результате чего между ними течёт ток, значение которого известно. На других клеммах прибора подключены два внутренних рабочих электрода.
На этих клеммах присутствует значение падения напряжения. Конечный результат по замерам – сопротивление заземления (в Омах), значение которого прибор демонстрирует на дисплее.
Приборами из серии 4500 часто пользуются для измерения напряжения прикосновения. Устройством при помощи специального модуля генерируется в земле напряжение небольшой величины – имитация повреждения кабеля.
Одновременно на шкале прибора указывается ток, текущий по цепи заземления. Показания на экране берут за основу и умножают на предполагаемую величину тока в земле. Таким способом вычисляют напряжение прикосновения.


Выполнение мероприятий по контролю за состоянием электротехнической аппаратуры и линий заземления. Для работы используется измерительный прибор типа 4500
К примеру, максимальное значение ожидаемого тока на участке повреждения равно 4000А. На экране прибора отмечается величина 0,100. Тогда величина напряжения прикосновения будет равна 400В (4000*0,100).
Измерение прибором С.А6415 (6410, 6412, 6415)
Уникальность этого способа – возможность проведения замеров без отключения заземляющей цепи. Также здесь следует выделить преимущественную сторону, когда измерять общее сопротивление устройства заземления допустимо методом включения в цепь заземления резистивной составляющей всех соединений.
Принцип работы примерно следующий:
- Специальным трансформатором в цепи создаётся ток.
- Ток течёт в образованном контуре.
- С помощью синхронного детектора регистрируется измеряемый сигнал.
- Полученный сигнал преобразуется АЦП.
- Результат выводится на ЖК-дисплей.
Устройство оснащается модулем (избирательный усилитель), благодаря которому полезный сигнал эффективно очищается от разного рода помех – н.ч. и в.ч. шумов. Лапами клещей в их сочленённом состоянии образуется возбуждаемый контур, охватывающий проводник заземления.
Инструкция измерения прибором С.А6415
Последовательность действий при работе с прибором серии С.А6415 доходчиво описывается в инструкции, прилагаемой к этому уникальному устройству.


Уникальный измерительный прибор – клещи, благодаря которому относительно просто и легко удаётся измерить сопротивление земляного контура в различных условиях
Например, есть необходимость провести измерения сопротивления заземления какого-либо электрического модуля (трансформатора, электросчётчика и т.п.).
Последовательность действий:
- Открыть доступ к заземляющей шине, сняв защитный кожух.
- Захватить клещами проводник (шину или непосредственно электрод) заземления.
- Выбрать режим измерения «А» (измерение тока).
Максимальное значение тока прибора составляет 30А, поэтому в случае превышения этой цифры выполнять измерение нельзя. Следует снять прибор и повторить попытку измерений в другой точке.


Процесс выполнения замеров с помощью измерительных устройств типа С.А6415 и 3770. Результаты измерений фиксируются в таблице и сравниваются при следующем ТО
Когда полученная на шкале величина тока укладывается в допустимый диапазон, можно продолжить работу переключением прибора на измерение сопротивления «?».
Высвеченный на дисплее результат покажет общее значение сопротивления, включая:
- электрод и шину заземления;
- контакт нейтрали с электродом заземления;
- контакт соединений на линии между нейтралью и заземляющим электродом.
Работая с клещами, следует иметь в виду: завышенные показания прибора по сопротивлению заземления, как правило, обусловлены плохим контактом заземляющего электрода с грунтом.
Также причиной высокого сопротивления может быть оборванная токоведущая шина. Высокие цифры сопротивлений в точках соединений (сращиваний) проводников тоже могут влиять на показания прибора.
Общие рекомендации по измерению УСГ
Прежде чем , к примеру для газового котла, следует получить точные сведения о том, в область каких грунтов будет закладываться заземляющий электрод. Часто для определения значений “p” грунта предлагается обращаться к существующим таблицам.
Однако этот вариант с таблицами даёт чисто ориентировочные данные. Поэтому полагаться на них не стоит. Истинные значения сопротивления грунта могут отличаться в разы.
Вариант #1: однослойный грунт
Если грунт имеет однородную составляющую, его удельное сопротивление измеряют методикой «пробного электрода».


Структура однородного грунта. При таких условиях измерить и вычислить сопротивление значительно проще, чем проделывать ту же самую работу на многослойных грунтах
Метод предполагает выполнение определённой процедуры в два этапа:
- Берут стержневой контрольный зонд длиной чуть больше глубины проектной закладки.
- Погружают зонд в землю строго вертикально на глубину проектной закладки.
- Оставшийся над поверхностью земли конец используют для замера сопротивления растекания (Rr).
- Определяют УСГ по формуле p = Rr * Ψ.
Желательно выполнить процедуру несколько раз в различных точках рабочей площадки. Альтернативные замеры помогают достичь точных результатов измерений сопротивления грунта.
Вариант #2: многослойный грунт
Для такой ситуации замер УСГ выполняют методом ступенчатого зондирования. То есть контрольный зонд погружается до рабочей глубины ступенями и в положении каждой ступени выполняются измерения удельного сопротивления. Вычисления среднего УСГ производятся с помощью формул для каждого отдельного измерения.


Многослойный грунт. При таких условиях приходится вычислять сопротивление каждого отдельно взятого слоя. Расчёты по многослойным грунтам требуют больше работы
Затем, исходя из климатических особенностей местности, находят значения для сезонных изменений. Таким способом (достаточно сложным) получают расчётные значения УСГ верхних слоёв. Нижележащие слои рассматриваются как не подверженные сезонным изменениям и потому расчёт для них ограничивается несколько упрощённым измерением и вычислением.
Требования к исполнению работ
Работы подобного плана, конечно же, выполняются квалифицированным персоналом, представляющим специализированные организации. Так, за эксплуатацию силовых щитков в жилых домах, как правило, отвечают коммунальные службы. Производить какие-либо измерения в этих точках разрешается только через обращение к этим службам.
Электрические цепи относятся к опасным системам. Несмотря на то, что коммуникации бытового сектора рассчитаны под напряжение менее 1000В, это напряжение смертельно для человека. Требуется соблюдать все необходимые меры безопасности при обращении с электрическим оборудованием. Обывателю зачастую такие меры попросту неведомы.
С особенностями сооружения заземления для ванны в городской квартире ознакомит , содержащая правила и руководство по проведению работы.
Выводы и полезное видео по теме
Выполнение измерений на практике с помощью прибора:
Исполнение работ, связанных с проверкой сопротивления заземления, требуется обязательно, независимо от сложности электрической схемы и категории объекта, где устанавливается или установлено и эксплуатируется электрооборудование. Многие специализированные организации готовы предоставлять такие услуги.
Оставляйте, пожалуйста, комментарии в расположенном ниже блоке. Не исключено, что вы знаете простой и эффективный способ измерения сопротивления контуров заземления, не приведенный в статье. Задавайте вопросы, делитесь полезной информацией и фото по теме.
Когда идет речь о вопросах безопасности людей предпочтительнее использовать методики измерений, хорошо зарекомендовавшие себя на протяжении десятилетий. Применительно к заземлению таким методом является измерение сопротивления с помощью комбинации амперметра и вольтметра (рекомендуемый ГОСТ Р 50571.16-2007). Иногда такой метод называют «трёхпроводным» (или «трёхзажимным»). Существует и более точная его модификация, именуемая «четырёхпроводным» («четырёхзажимным») методом. Как правило, оба метода могут быть реализованы в одном измерительном приборе.

Измерение сопротивления заземления по методу амперметра-вольтметра
При проведении измерений данным методом заземление отключается от электроустановки. На расстоянии не менее 20 м от исследуемого заземления в землю вкапывается потенциальный штырь. На расстоянии не менее 40 м от исследуемого заземления вкапывают токовый штырь. Штыри и заземление должны быть расположены на одной линии. Конкретные рекомендации по расстояниям между заземлением и штырями могут отличаться в зависимости от типа заземления и модели применяемой измерительной аппаратуры. Как правило, такие рекомендации указываются в инструкции к измерительной установке.
На контур, образованный исследуемым заземлением, токовым штырем и амперметром, через трансформатор передается переменный ток. В современных приборах это обычно не синусоида с частотой 50 Гц, а меандр с частотой порядка 100 — 200 Гц. Тем самым проверяется работоспособность заземления на гармониках высшего порядка и удается частично сократить влияние помех. При помощи вольтметра измеряется напряжение между заземлением и потенциальным штырем. Далее на основе закона Ома вычисляется сопротивление заземления по формуле:
R = U/I,
где U – напряжение между заземлением и потенциальным штырем, а I – сила тока в контуре, образованном заземлением, токовым штырем, трансформатором и амперметром.
Общая проблема классических методов измерения сопротивления заземления — влияние блуждающих токов в почве.
Метод амперметра-вольтметра на практике имеет две разновидности: трёхпроводный и четырёхпроводный методы, о которых и пойдет далее речь.
Трёхпроводный метод
Обозначим клеммы для измерения напряжения как П1 и П2, а клеммы для измерения тока — как T1 и T2. В реально существующих измерительных приборах эти клеммы могут иметь иные обозначения.

Схема измерения трёхпроводным методом
При трёхпроводном методе клеммы П1 и T1 соединяются перемычкой и подключаются одним проводом к исследуемому заземлению. Клемма П2 соединяется проводом с потенциальным штырем, а клемма П1 — с токовым штырем.
Преимуществом трёхпроводного метода является меньшее количество проводов. Недостатком — сильное влияние сопротивления провода, идущего к заземлению, на результаты измерения. Поэтому, обычно, трёхпроводный метод применяется для измерения сопротивления заземления, значение которого заведомо выше 5 Ом.
Четырёхпроводный метод
Когда к точности измерений предъявляются более высокие требования, используется четырёхпроводный метод. При нем к исследуемому заземлению идут раздельные провода от клемм П1 и T1, которые соединяются только непосредственно на клеммах заземления.

Схема измерений четырёхпроводным методом
Через провод, который идет к T1, течет ток. Образующаяся при этом разность напряжений на концах провода вносит погрешность в измерения, характерные для трёхпроводного метода. Но при четырёхпроводном методе точка измерения напряжения (на клеммах заземления) соединена с измерительным прибором отдельным проводом. По этому проводу течет пренебрежимо малый ток (не более единиц миллиампер), так что его сопротивление практически не вносит погрешности в измерения.
Повышение точности измерений
Классический способ измерения сопротивления заземления чувствителен к неравномерности свойств почвы в разных местах. Поэтому для повышения точности измерения рекомендуется несколько раз поменять расположение потенциального штыря с шагом, примерно равным 10% от его номинального расстояния до заземления. Разброс измеренных значений не должен быть больше 5%. Если он больше, то расстояние между исследуемым заземлением и штырями увеличивают в 1,5 раза или меняют направление линии, по которой расставлены штыри.
Выбор измерителя сопротивления заземления
До сих пор в литературе для классического метода измерения сопротивления рекомендуются приборы еще советской разработки. Но они уже не соответствуют современным реалиям, ведь электрооборудования в наших домах с тех пор стало намного больше. Появились новые устройства (например, базовые станции мобильной связи), предъявляющие особые требования к заземлению. Поэтому есть смысл обратиться к продукции ведущих мировых брендов. Но и здесь не все так просто — цены зачастую «кусаются», да и могут быть расхождения в отечественных и зарубежных нормах.
Оптимальным вариантом представляется измерительная аппаратура, выпущенная в Китае на основе самых современных технологий, но по спецификациям и под локальным брендом российской компании. Например, ЖГ-4300 (аббревиатура расшифровывается как «Железный Гарри»). Это устройство позволяет измерять сопротивление заземления в пределах от 0,05 Ом до 20,9 кОм. Доступно измерение по двух- трёх- и четырёхпроводному методам. Напряжение на клеммах не превышает 10 В, что позволяет проводить измерения с высоким уровнем электробезопасности. Прибор не просто соответствует российским нормам, он включен в Государственный реестр средств измерений. При этом цена раза в 3 ниже, чем у аналогов от известных зарубежных брендов.
Другие способы измерений
Более простым в использовании, но при этом менее точным является двухпроводный метод измерения сопротивления заземления. Он позволяет быстро получить оценку сопротивления, что бывает ценным, например, при проведении ремонтных работ. Об этом методе рассказывается в отдельной статье (ссылка).
Дальнейшим развитием классического метода измерения стал так называемый компенсационный метод. Он позволяет чисто аналоговыми способами отстроиться от помех, вызванных блуждающими токами. Недостатком данного метода является сложность настройки прибора и более высокие требования к квалификации оператора, поэтому большой популярности он не завоевал.
Также существует семейство безэлектродных методов измерения, позволяющих не отключать заземление от электроустановки. Они основаны на использовании токовых клещей. Метод, основанный на применении двух клещей также относится к рекомендованным ГОСТ Р 50571.16-2007. Недостатком такого метода является то, что он может напрямую применяться только в системах ТТ и системах TN с ячеистым заземлением. Для обычных систем TN потребуется кратковременная установка перемычки между нейтралью и заземлением, что потенциально представляет угрозу электробезопасности, так что питание во всем здании, где установлено заземление, придется на время измерений отключить.
Выводы
И в цифровую эпоху классический метод вольтметра-амперметра является основным для измерения сопротивления заземлений. Накоплен большой опыт его применения, поэтому его можно считать надежным. Цифровые технологии позволяют мгновенно вычислить значение сопротивления и сразу увидеть результат на дисплее измерительного прибора. Кроме этого, с помощью современных технологий удается в значительной степени подавлять помехи при измерениях. Благодаря этому точность измерений может быть доведена до 1 — 2%, что позволяет классическим методам успешно конкурировать с методами, основанными на использовании токовых клещей, погрешность у которых заметно выше.
Обзор методик
Метод амперметра-вольтметра

Чтобы измерить сопротивление методом амперметра-вольтметра необходимо воспользоваться законом Ома. Итак, по формуле R=U/I находим сопротивление контура заземления. Такой метод хорошо подходит для измерений в частном доме. Чтобы получить нужный измерительный ток можно воспользоваться сварочным трансформатором. Также подойдут и другие виды трансформаторов, вторичная обмотка которых электрически не связана с первичной.
Использование специальных приборов
Сразу отметим, что даже для измерений в домашних условиях многофункциональный мультиметр не сильно подойдет. Чтобы измерить сопротивление контура заземления своими руками используются аналоговые приборы:
- МС-08;
- М-416;
- ИСЗ-2016;
- Ф4103-М1.
Рассмотрим, как измерить сопротивление прибором М-416. Сначала нужно убедиться, что у прибора есть питание. Проверим наличие батареек. Если их нет, нужно взять 3 элемента питания напряжением 1,5 В. В итоге получим 4,5 В. Готовый к использованию прибор нужно поставить на ровную горизонтальную поверхность. Далее калибруем прибор. Ставим его в положение «контроль» и, удерживая красную кнопку, выставляем стрелку на значении «ноль». Для измерения будем пользоваться трехзажимной схемой. Вспомогательный электрод и стержень зонда забиваем не менее чем на полметра в грунт. Подсоединяем к ним провода прибора по схеме.

Переключатель на приборе устанавливается в одно из положений «Х1». Зажимаем кнопку и крутим ручку, пока стрелка на циферблате не сравняется с отметкой «ноль». Полученный результат необходимо умножить на ранее выбранный множитель. Это и будет искомое значение.
На видео наглядно демонстрируется, как измерить сопротивления заземления прибором:
Также могут быть использованы более современные цифровые приборы, которые намного упрощают работы по замерам, более точны и сохраняют последние результаты измерений. Например, это приборы серии MRU – MRU200, MRU120, MRU105 и др.
Работа токовыми клещами
Сопротивление контура заземления можно измерять также токовыми клещами. Их преимущество в том, что нет необходимости отключать заземляющее устройство и применять вспомогательные электроды. Таким образом, они позволяют достаточно оперативно вести контроль за заземлением. Рассмотрим принцип работы токовых клещей. Через заземляющий проводник (который в данном случае является вторичной обмоткой) протекает переменный ток под воздействием первичной обмотки трансформатора, которая находится в измерительной головке клещей. Для расчета величины сопротивления необходимо разделить значение ЭДС вторичной обмотки на величину тока, измеренную клещами.
В домашних условиях можно использовать токовые клещи С.А 6412, С.А 6415 и С.А 6410. Более подробно узнать о том, как пользоваться токоизмерительными клещами, вы можете в нашей статье!
Безэлектродный способ
Этот метод является наиболее современным и позволяет измерять сопротивление контура, не прибегая к размыканию заземляющих стержней и установке дополнительных заземляющих электродов. В связи с этим условием, метод имеет ряд дополнительных преимуществ:
- возможность производить замеры в полевых условиях, в тех местах, где невозможно применить другие методы измерения сопротивления;
- экономия времени и средств для выполнения работ.
Безэлектродный метод может применяться, если используются двое измерительных токовых клещей. Например, это могут быть современные тестеры типа Fluke 163. Клещи располагают вокруг заземляющего электрода или соединительного кабеля. Клещами при этом измеряется индуцируемое напряжение. Его амплитуда фиксируется вторыми клещами.
Тестер автоматически определяет сопротивление контура заземления для данного соединения.
Периодичность измерений
Проводить визуальный осмотр, измерения, а также при необходимости частичное раскапывание грунта нужно согласно графику, который установлен на предприятии, но не реже чем один раз в 12 лет. Получается, что, когда производить замеры заземления – решать вам. Если вы живете в частном доме, то вся ответственность лежит на вас, но не рекомендуется пренебрегать проверкой и замерами сопротивления, так как от этого напрямую зависит ваша безопасность, при пользовании электрооборудованием.

При проведении работ необходимо понимать, что в сухую летнюю погоду можно добиться наиболее реальных результатов измерений, так как грунт сухой и приборы дадут наиболее правдивые значения сопротивлений заземления. Напротив, если замеры будут проведены осенью либо весной в сырую, влажную погоду, то результаты будут несколько искажены, так как мокрый грунт сильно влияет на растекаемость тока, что, в свою очередь, дает большую проводимость.
Если вы хотите, чтобы измерения защитного и рабочего заземления проводили специалисты, то необходимо обратиться в специальную электротехническую лабораторию. По окончании работы вам будет выдан протокол измерения сопротивления заземления. В нем отображается место проведения работ, назначение заземлителя, сезонный поправочный коэффициент, а также на каком расстоянии друг от друга находятся электроды. Образец протокола предоставлен ниже:

Напоследок рекомендуем просмотреть видео, в котором показывается как измеряют сопротивление заземления опоры ВЛ:
Вот мы и рассмотрели существующие методики измерения сопротивления заземления в домашних условиях. Если вы не обладаете соответствующими навыками рекомендуем воспользоваться услугами специалистов, которые все сделают быстро и качественно!
Также рекомендуем прочитать:
Система заземления представляет собой соединение электрического оборудования с грунтом для отвода тока. Заземлительные устройства обеспечивают защиту обитателей здания и находящегося в нем имущества от разрушительного воздействия электричества. Чтобы удостовериться в необходимой функциональности системы, проводится периодическая проверка заземления.
Зачем замерять сопротивление
Измерения необходимы для определения величины сопротивления заземлительного контура. Также измеряют показатель сопротивления изоляционного слоя. Показатели должны находиться в рамках нормативов, разработанных контролирующими органами. В случае надобности сопротивление заземляющего устройства уменьшается увеличением поверхности контакта или улучшением общей проводимости среды. Для достижения нужного результата увеличивают число электродов или создают соленую среду в почве вокруг заземлителя.


Типы заземления
Существует два типа заземления:
- Предотвращение последствий от ударов молнии. Заземление молниеприемниками для отвода тока по металлической конструкции в землю.
- Защитное заземление корпусов электробытовой техники или не токопроводящих участков электроустановок. Предотвращает поражение электричеством при случайном касании к элементам, не предназначенным для пропускания тока.
Электричество на электроустановках, где не должно появляться напряжение, возникает в таких ситуациях:
- статическое электричество;
- наведенное напряжение;
- вынос потенциала;
- электрический заряд.
Система заземления представляет собой контур, созданный из металлических прутьев, закопанных в грунт, вместе с подключенными к нему проводящими элементами. Точкой заземления называют место стыковки с заземляющим устройством проводника, идущего от защищаемой техники.


Заземлительная система подразумевает контакт устройства заземления с корпусами электробытовой техники. Причем заземление не работает до тех пор, пока по любой причине не возникнет потенциал. В исправной цепи не появляются никакие виды токов за исключением фоновых. Основной причиной появления напряжения является нарушение изоляционного слоя на оборудовании или повреждение проводящих элементов. При возникновении потенциала происходит его перенаправление в грунт посредством заземляющего контура.
к содержанию ↑Заземлительная система уменьшает напряжение на нетоковедущих металлических участках до приемлемого (безопасного для живых существ) уровня. В случае если целостность контура по каким-либо причинам нарушена, напряжение на нетоковедущих элементах не снижается, а потому представляет серьезную опасность для человека и домашних животных.
Факторы учета сопротивления
Для тестирования соответствия заземляющего устройства требованиям нормативов осуществляется замер сопротивления растеканию тока Rз. В идеале данный показатель должен быть равен нулю. Однако в реальности эта цифра недостижима.
Величина (Rз) включает в себя несколько компонентов:
- Сопротивление материала, установленного под землей электрода, а также сопротивление на контакте металла с проводником. Однако этот показатель не столь важен из-за отличной проводимости используемых материалов (сталь с напылением меди или же чистая медь). Показатель игнорируется только в случае качественного соединения с проводником.
- Сопротивление между почвой и электродом. Показатель игнорируют, если электрод плотно установлен, а контакт не покрашен или не покрыт диэлектриком. Однако с течением времени металл ржавеет, и его проводимость уменьшается. Поэтому следует использовать покрытые медью стержни или делать замеры сопротивления растеканию. Для уменьшения интенсивности коррозии сварочные швы лакируют.


- Сопротивление грунта. Считается самым важным фактором. Особое значение придается близлежащим слоям почвы. По мере удаления слоев сопротивление уменьшается. На определенном расстоянии сопротивление становится нулевым.
- Неоднородность электрических характеристик грунта с трудом поддается учету. Исходя из этого замеряют фактический Rз. Для одиночной простой заземлительной конструкции определяющее значение имеют поверхностные слои земли, а для контурной — глубинные.
к содержанию ↑
Объект испытания
Проверочные действия осуществляются в отношении заземлительных устройств, выполненных как одиночные электроды или контуры. К объектам проверки не относятся PEN-проводники и PE-проводники, включенные отдельными жилами в кабели.
Заземлительные устройства создаются в одном из двух исполнений:
- Горизонтальное. В этом случае полосы располагаются по дну траншеи.
- Вертикальное. Заземлительный контур представляет собой забитые в землю и соединенные между собой полосы или трубы. Стержни располагают в грунте на глубине, превышающей длину самих металлических изделий. Чаще всего контур по своей форме создается в виде треугольника.
Замена элементов системы осуществляется при ржавлении более 50% поверхности. Проверка на коррозию на электроустановках проводится выборочно там, где наиболее заметны ее проявления. При проведении проверочных мероприятий тестируют заземление нейтралей. На высотных линиях проверяют по крайней мере 2% от имеющихся опор. Предпочтительные объекты проверок — участки заземления, находящиеся в максимально агрессивных средах.
В таблице внизу представления показатели Rз, присущие разным видам заземлителей.


Проведение замеров
Метод амперметра-вольтметра
Чтобы провести замеры, создают электрическую цепочку, по которой ток протекает через проверяемое заземлительное устройство и токовый проводник (его также именуют вспомогательным электродом). В схеме присутствует еще и потенциальный электрод, задача которого состоит в измерении падения напряжения при протекании тока через заземлитель. Потенциальный проводник находится на участке с нулевым потенциалом — на равном удалении от вспомогательного электрода и проверяемой заземлительной системы.
к содержанию ↑Для измерений сопротивления применяют закон Ома (формула R=U/I). С помощью данной методики чаще всего определяют сопротивление в условиях частного дома. Для получения необходимого тока используют трансформатор для сварочных работ или любое другое оборудование, где отсутствует электрическая связь между вторичной и первичной обмоткой.
Использование специальной техники
В домашних условиях редко пользуются дорогостоящим многофункциональным мультиметром. Чаще всего применяются аналоговые приборы:
- МС-08;
- Ф4103-М-1;
- М-416;
- ИСЗ-2016.


Один из самых распространенных приборов для проверки сопротивления — МС-08. Для измерений устанавливают два электрода на 25-метровом расстоянии от заземлительного устройства. Ток в цепочке образуется под действием генератора, вращаемого вручную с помощью редуктора. В результате задействования схемы и подключения прибора происходит компенсация сопротивления вспомогательных заземлителей. Если этого не случается, почва возле дополнительного заземлительного устройства искусственно увлажняется. Замеры осуществляют в различных диапазонах до тех пор, пока тестер не покажет значимых показателей (причем они не должны разниться после окончательной установки).
Измерительный прибор М-416 комфортен в использовании благодаря малому весу и шкале, где фиксируются полученные данные. М-416 включает в себя полупроводники с автономным электропитанием.
Пример использования прибора М-416:
- Проверяем наличие питания у прибора. В устройстве должны находиться три батарейки — каждая по 1,5 вольта.
- Устанавливаем прибор на ровную поверхность.
- Проводим калибровку оборудования. Настраиваем М-416 на контроль и, нажимая на красную кнопку, устанавливаем стрелку на нулевое положение.
- Выбираем трехзажимную схему для проведения замера.
- Вспомогательный проводник и стержень зонда вкапываем в землю по меньшей мере на 50 сантиметров.
- Соединяем провода с электродом и стержнем зонда согласно схеме.
- Переключатель ставим в одну из позиций «X1». Удерживая клавишу, прокручиваем ручку до тех пор, пока стрелка на шкале не достигнет нуля. Результат умножаем на ранее вычисленный множитель. Итоговое значение является искомым.


Работа токовыми клещами
Контурное сопротивление определяют также с помощью токовых клещей. Их основное достоинство том, что не нужно отключать заземлитель и использовать вспомогательные проводники.
Через проводник заземления, в роли которого выступает вторичная обмотка, проходит переменный ток. Протеканию тока способствует первичная трансформаторная обмотка, находящаяся в измерительной головке устройства. Чтобы определить показатель сопротивления, делим данные ЭДС вторичной обмотки на величину тока, полученную при измерении клещами.
В качестве примера токовых клещей приведем тестер СА 6415. Он оснащен жидкокристаллическим монитором. Для измерения сопротивления не нужны дополнительные проводники. Также отсутствует потребность в отключении PE-проводника от электродов.


Замер сопротивления изоляции
Чтобы измерить сопротивление изоляции, используют специальный прибор — мегомметр. Устройство состоит из нескольких элементов:
- генератор непрерывного тока, оснащенный ручным приводом;
- добавочные сопротивления;
- магнитоэлектрический логометр.
До начала проверочных работ следует удостовериться, что объект отключен от электропитания. Удаляем с изоляционного слоя пыль и грязь. После этого проводим замер в течение приблизительно 3 минут. В результате получаем данные по остаточным зарядам.
К электроцепи или оборудованию мегомметр подключаем отдельными проводниками. Изоляция отличается высоким сопротивлением. Его уровень чаще всего превышает 100 мегаом.


к содержанию ↑Обратите внимание! Замер сопротивления изоляции проводится после того, как стрелка займет устойчивую позицию.
Периодичность измерений
Определение периодичности замеров сопротивления заземлительного устройства осуществляется в соответствии с требованиями ПТЭЭП (Правила технической эксплуатации электроустановок потребителей). Согласно регламенту, проверки производят каждые 6 лет. Также осуществляются регулярные проверки исправности контура. Визуальный осмотр наружных частей и частичное откапывание внутренних элементов контура делают по установленному на объекте графику, но не реже одного раза в год.
Указанные сроки относятся к предприятиям. Регулярность проверок в частных домах оставляется на усмотрение владельцев. Специалисты не рекомендуют пренебрегать проверочными мероприятиями, поскольку от этого зависит безопасность проживания в доме.
В теплую и сухую погоду результаты испытаний более достоверны. А вот во влажной среде они будут не столь точными, поскольку растекаемость тока приводит к повышению проводимости.
Нормативные результаты испытаний указаны в таблице ниже.


Оформление результатов проверки
Если решено поручить проверку специалистам, следует обратиться в специализированную электротехническую лабораторию. Проверку выполнят квалифицированные сотрудники. По результатам работы будет выдан протокол измерения сопротивления.
Протокол представляет собой бланк, в котором указаны такие данные:
- место проведения испытаний;
- название проверяемого объекта;
- назначение заземлительного устройства;
- схема установки заземлителей и их соединений;
- расстояние между электродами.
Кроме того, в протоколе указывается сезонный поправочный коэффициент и методика, в соответствии с которой осуществлялось измерение. Для составления протокола необходим паспорт объекта и акт на скрытые работы.
Обратите внимание! Рекомендуется включать в протокол данные о приборе, с помощью которого измерялось сопротивление. Информация должна включать тип устройства, его заводской номер и другие важные показатели. Результаты измерений вносят в паспорт заземлителя.
Отдельно составляется протокол испытания переходных сопротивлений. Данное понятие (переходное сопротивление также называют металлосвязью) представляет собой потенциальные потери на пути протекания тока. Они происходят в связи с наличием на контуре каких-либо соединений, в том числе сварочных, болтовых и прочих. Испытательные работы проводят с помощью специального тестера — микроомметра.
Правом проведения официальных испытаний и выдачи протокола обладает только сертифицированная органом стандартизации испытательная лаборатория. После выдачи акта система считается пригодной к эксплуатации.
Измерение сопротивления заземления: методы, приборы и периодичность

Параметры заземления зависят от множества факторов, и не все их можно учесть при расчетах. Поэтому после установки заземления рекомендуется многократно измерить его сопротивление в разные времена года. Элементы заземления могут окисляться и подвергаться коррозии, поэтому также необходимо периодически измерять сопротивление заземления и после того, как вы убедились, что все было сделано правильно. Действующие в России нормы требуют измерять сопротивление заземления электроустановок не реже, чем раз в 12 лет. Для опор воздушных линий, имеющих разъединители, защитные промежутки, разрядники, повторное заземление нулевого провода, измерение сопротивления заземления осуществляется ежегодно. Также ежегодно выборочно измеряют параметры заземления у 2% металлических и железобетонных опор воздушных ЛЭП, проходящих в населённых местностях.
Классические способы измерения сопротивления подразумевают установку дополнительных заземляющих штырей (электродов) на расстоянии порядка 20 м от исследуемого заземления. Это может представлять проблему, если в процессе измерения штыри придется устанавливать на территории, принадлежащей собственнику. Кроме этого, могут возникнуть проблемы с установкой дополнительных штырей зимой в промерзший грунт. А ведь именно ситуация с промерзанием является наиболее проблематичной с точки зрения функционирования заземления. Например, в районах вечной мерзлоты ПТЭЭП предписывает проводить измерение сопротивления заземления ЛЭП только в период наибольшего промерзания грунта. Другим недостатком традиционных способов измерения сопротивления является необходимость отключать параллельно подключенные заземления.
Перечисленные обстоятельства делают актуальным применения так называемых безэлектродных методов измерения сопротивления заземления, не требующих устанавливать в землю дополнительные штыри. Это стало возможным благодаря современным токовым клещам.
Принцип безэлектродного метода измерения сопротивления заземления заключается в следующем. На заземление от измерительного генератора подается переменный ток заданного напряжения с частотой, отличной от частоты сети. Сила тока в заземлении измеряется специальными токовыми клещами с фильтром, который делает их чувствительными только к частоте, на которой работает измерительный генератор. По полученным данным измерения тока стекающего в заземлитель, основываясь на известном значении напряжения, поданного на заземление, специализированные клещи автоматически вычисляют сопротивление.

Безэлектродная схема измерения сопротивления заземления с применением токовых ключей
Напряжение на заземление подается с помощью других токовых ключей. Они используются как генератор и трансформатор, подводящий электроэнергию к заземлению. Наиболее современные модели совмещают излучающий и измерительные трансформаторы в единой конструкции, что позволяет использовать только одни клещи.
Пример клещей для измерения сопротивления заземления
Преимущества безэлектродного способа измерения сопротивления заземления особенно явно проявляются, если использовать легкие и компактные приборы. Например, Fluke 1630, размеры которого составляют всего 276 x 100 x 47 мм, а вес — 750 г. Питается прибор от автономного источника (щелочной батареи), время работы без замены батареи составляет 8 ч. В приборе используются только одни клещи, достаточно обхватить ими провод или шину, ведущие к заземлению, и через 0,5 с на дисплее появится значение сопротивления.

Измеритель сопротивления заземления Fluke 1630
Прибор способен измерять сопротивление заземления в диапазоне от 0,025 до 1500 Ом. Этот диапазон разбит на 7 поддиапазонов, выбор которых осуществляется автоматически. Столь широкий диапазон позволяет использовать прибор не только для измерения сопротивления заземления, но и сопротивления утечки.
Кстати, Fluke-1630 может использоваться и как обычные токовые клещи, измеряя ток силой до 4 А.
Интерпретация результатов измерений
Точность измерения сопротивления, не превышающего 100 Ом прибором Fluke 1630 составляет не более +/- 1,5%. Но здесь важно понимать, какое именно сопротивление мы измеряем.

Эквивалентная схема цепи
Рассмотрим эквивалентную схему цепи. Из нее видно, что измеряется сопротивление электрической цепи Rs, в которую входят другие заземления и собственно земля.
Измерительные клещи выдают значение, рассчитанное по формуле:
Rs = E/I,
где E — напряжение, индуцированное в проводнике, а I — измеренный ток.
При этом,
Rs = Rg + Rz + 1/(1/R1 + 1/R2 + … 1/Rn),
где Rg – сопротивление исследуемого заземления, Rz – сопротивление почвы, n – количество заземлений, подключенных параллельно к исследуемому.
Сумма Rz и общего сопротивления включенных параллельно заземлений много меньше максимально допустимого значения сопротивления заземления (4 — 8 Ом). Поэтому принимают, что
Rg ≈ Rs,
причём в реальности Rg < Rs.
Для измерений используется частота около 3 кГц. Это также может стать источником погрешности, так как на этой частоте уже начинает сказываться индуктивность проводов. Но, опять-таки, наличие у проводов индуктивности вносит погрешность в сторону увеличения сопротивления.
Можно сделать вывод, что метод безэлектродного измерения сопротивления заземления дает оценку параметра сверху. Если вы получили определенный результат, то можете быть уверены, что в реальности сопротивление заземления будет немного ниже. Это очень важно с точки зрения безопасности, так как погрешность метода принципиально не может привести к заниженной оценка сопротивления, когда неисправное заземление будет оцениваться как исправное.
Смотрите также:
что это такое, чем и как его измерять
Что такое заземление.
Заземление – это намеренное соединение частей и узлов электрооборудования, не находящихся в нормальном состоянии под напряжением с электродом, установленном в земле. При этом необходимо обозначить такое понятие как сопротивления растеканию.
При замыкании на землю, по мере удаления от электрода потенциал будет падать и, в конце концов, станет нулевым. Таким образом, сопротивление растеканию заземлителя – это параметр характеризующий сопротивление земли в месте установки электрода. Понятие сопротивления растеканию особенно актуально в сетях выше 1000 В.
Для чего нужно заземление.
Заземление необходимо для предотвращения поражения человека воздействием электрического тока, в случае его появления там, где при нормальных условиях его не должно быть. При касании корпуса прибора, находящимся под напряжением, сила тока, проходящего через тело человека, может оказаться смертельной.
Необходимостью снижения разности потенциалов и обусловлено применение защитного заземления. Кроме этого, замыкание на землю приводит к увеличению силы тока и, как следствие, к срабатыванию защитных устройств. Нормы сопротивления защитного заземления регламентируются ПУЭ, а также документом называемым «Правила и нормы испытания электрооборудования».
Конструкция заземления.
Заземление – это комплекс технических устройств защитного типа, состоящий из:
- Заземлителя — одного или нескольких вертикальных проводников (стержней), имеющих электрический контакт с землей и связанных между собой.
- Заземляющего проводника (путь для тока замыкания), соединяющего заземляемый объект и заземлитель.
На каждое заземление составляется паспорт. В паспорт заносится схема заземляющего устройства (длина, и схема расположения электродов контура), тип, удельное сопротивление грунта, а также результаты замера сопротивления заземления. Обязательным приложением к паспорту является акт на скрытые работы. Данный акт необходим в связи с тем, что большая часть заземляющего устройства находится под землей и этот акт представляет собой схему расположения элементов заземляющего устройства. В случае, если паспорт на заземление отсутствует, эксплуатация объекта запрещена.
Методика измерения сопротивления защитного заземления.
Для проверки сопротивления заземления используется метод амперметра-вольтметра, заключающийся в том, что через измеряемое сопротивление течет ток определенной величины и одновременно измеряется падение напряжения. Разделив значение тока на величину падения напряжения, получаем значение сопротивления. В принципе, под понятием измерения сопротивления заземления, подразумевается измерение сопротивления растеканию. Правила и нормы испытаний электрооборудования задают минимальное сопротивление заземления, рассчитанные с точки зрения безопасности. Нормы различаются в зависимости от типов электроустановок (глухозаземленная или изолированной нейтралью). Класс использованного напряжения также влияет на нормы сопротивления.
Приборы для измерения заземления.
Бытовой тестер для такой проверки использовать нельзя, так как он не способен генерировать достаточно высокое напряжение. Для измерений используется, как приборы уже давно выпускающиеся (МС-08, М-416 и др.), так и новые средства измерения, выполненные на современной электронной базе и характеризующиеся малым потреблением тока от источника питания. В настоящее время измерение защитного заземления можно выполнить также цифровым мультиметром или специальным тестером.
Порядок проведения измерения заземления (сопротивления растеканию заземлителя).
Для проведения проверки необходимо помимо прибора иметь два электрода (токовый и потенциальный) с проводами достаточной длины, как образец, можно предложить отрезок гладкой арматуры или трубы круглого сечения.
В зависимости от сложности конструкции заземлителя, измерение сопротивления проводят по двум разным схемам:
- Простой (одиночный) заземлитель.
Применяется «линейная» схема подключения электродов. Потенциальный электрод устанавливают на расстоянии не менее 20 м. от заземлителя, а токовый не менее, чем в 10-12 м. от потенциального. - Сложный заземлитель.
Используется, когда простая схема неприменима, ввиду того, что при расчетах сопротивление заземления она не будет соответствовать минимально допустимым нормам. Представляет собой несколько вертикальных стержней вбитых в землю, электрически связанных между собой (электросваркой, чтобы снизить переходное сопротивление). Такое устройство называется контуром заземления. В этом случае необходимо определить наибольшее расстояние (диагональ) защитного контура заземления. Потенциальный электрод нужно вбивать на расстоянии равным пяти диагоналям от места присоединения заземляющего проводника. Токовый зонд забивается не менее, чем в 20 м. от потенциального. Измерительный прибор необходимо располагать как можно ближе к выводу заземления.
Порядок проведения измерений.
Так как в настоящее время самый распространенный прибор для проведения измерения является измеритель сопротивления заземления М-416, в дальнейшем, как образец, будет рассматриваться именно это средство измерений. Данный прибор относится к системе, в которой принцип измерений основан на компенсационном методе.
Запрещается для проверки пользоваться приборами, не имеющих действующего клейма о поверке, результаты которой должны заноситься в паспорт на средство измерения.
- Проверить наличие элементов питания в батарейном отсеке, убедившись, что их напряжение находится в пределах нормы;
- Откалибровать прибор, установив переключатель диапазонов в положение 5 Ом (контроль), ручкой реохорда установить стрелку как можно ближе к нулевой отметке. При этом на шкале должны быть показания 5 Ом;
- Отсоединить контур от заземляющего проводника;
- Присоединить прибор к соответствующим электродам;
- Тщательно зачистив вывод измеряемого заземлителя (для того чтобы исключить влияние, которое может оказать на конечный результат переходное сопротивление), присоединить к нему прибор.
Примечание: В зависимости от планируемых показателей сопротивления заземления измерение прибор нужно подключать по двух- или четырехпроводной схеме. Первая применяется, если предполагаемое сопротивление более 5 Ом, а вторая для измерения более низких значений (при этом разделяются пути прохождения тока и измерения разности потенциалов, для исключения влияния сопротивления присоединяемых проводов при измерении). В этом случае присоединение к заземлителю осуществляется двумя проводниками. Паспорт прибора содержит наглядные рисунки, которые позволят произвести подключения без ошибок.
- Установить переключатель диапазонов в положение, соответствующее наибольшей чувствительности (Х1), нажав кнопку «Измерение», регулятором установить стрелку на нуль. При этом на шкале реохорда будет отражен искомый результат проверки сопротивления заземлителя. Если стрелка не устанавливается на нуль, необходимо переключателем выбрать другой диапазон и показания реохорда умножить на соответствующий множитель.
Примечание: Если измерение проводится тестером или мультиметром, необходимость выбора множителя отпадает — эти приборы обладают функцией автоматического выбора предела шкалы.
ВАЖНО! После проведения измерений, если сопротивление заземления в пределах нормы необходимо вновь присоединить заземляющий проводник к заземлителю!
Оформление результатов измерений (протокол).
После окончания измерений нужно оформить протокол результата замера. Протокол представляет собой бланк определенной формы, в котором отражаются наименование объекта, схема установки заземляющих стержней и их соединений (для этого понадобится паспорт объекта и акт на скрытые работы). Также протокол должен отражать схему контура заземления и метод, по которому проводилось измерение. В протокол необходимо включить графу, в которой указан прибор или тестер (его тип, заводской номер и пр.), которым проводилось испытание. Результаты, полученные при измерении, заносятся в паспорт заземляющего устройства.
Отдельно представляется протокол испытания переходных сопротивлений. Переходное сопротивление (также, его еще называют металлосвязью) – это возможные потери на пути прохождения тока, связанные со сварочными, болтовыми и др. соединениями всего контура заземления. Это испытание проводится специальным тестером – микроомметром.
ВАЖНО! Проводить испытания и выдавать протокол измерения сопротивления заземления может только испытательная лаборатория, аккредитованная в системе органов стандартизации.
После окончания измерений составляется соответствующий акт, и заземляющее устройство считается годным к эксплуатации.
Контур заземления – важный элемент защитного электрооборудования. Он соединяется с системой выравнивания потенциалов строительного объекта и всеми корпусами электроприборов, оберегая людей от получения электротравмы при соприкосновении с токопроводящей цепью. Для соблюдения требований безопасности нужно периодически проверять состояние и эффективность заземляющих устройств.
Как работает заземление
Заземление обеспечивает уменьшение напряжения между электроустановкой и землей до безопасного уровня. При нормальной работе электрооборудования и цепей через контур проходят только малые фоновые токи. При пробое изоляционного слоя проводки на корпусе оборудования возникает высокое напряжение. Оно отводится через контур по РЕ-проводнику на потенциал земли. В итоге напряжение на нетоковедущих поверхностях оборудования уменьшается до безопасного значения.
При повреждении заземляющих устройств напряжение не отводится. Если при этом человек окажется между потенциалами неисправного электроприбора и землей, через его тело будет проходить ток. Поэтому во избежание электротравм при эксплуатации электрического оборудования важно поддерживать эффективность заземления и периодически проверять его состояние.

Причины проблем с сопротивлением заземления
В нормально работающем контуре ток в аварийной ситуации по РЕ-проводнику идет на контактирующие с грунтом токоотводящие электроды. Общий поток равномерно делится на составляющие и следует на потенциал земли. Но продолжительное пребывание тоководов в агрессивной среде грунта приводит к окислению металла и появлению на его поверхности окисной пленки.
Из-за коррозийных явлений ухудшается протекание тока, и увеличивается электрическое сопротивление контактов. Коррозия в виде отстающих от металлической поверхности чешуек нарушает локальный электрический контакт. При дальнейшем коррозийном повреждении тоководов сопротивление контура возрастает, заземляющее устройство становится менее проводимым и не справляется со своими задачами. Для выяснения состояния контура заземления выполняются замеры сопротивления заземляющих устройств.
Цель замеров сопротивления ЗУ
 Качество заземления характеризуется величиной сопротивления протеканию тока. Чем ниже это значение, тем лучше справляются со своими задачами заземляющие устройства. Основные способы уменьшения сопротивления – увеличение площади заземляющих электродов и уменьшение удельного электрического сопротивления почвы.
Качество заземления характеризуется величиной сопротивления протеканию тока. Чем ниже это значение, тем лучше справляются со своими задачами заземляющие устройства. Основные способы уменьшения сопротивления – увеличение площади заземляющих электродов и уменьшение удельного электрического сопротивления почвы.
Чтобы снизить сопротивление, можно увеличить число или глубину заземляющих электродов. Измерение сопротивления заземляющих устройств помогает минимизировать риск аварий, поломки электроустановок и нанесения урона здоровью или жизни людей.
Типы заземляющих устройств
Есть 3 вида заземления:
— Рабочее – определенные точки электрической цепи соединены с землей. Этот тип заземления осуществляется при помощи прибивных предохранителей, резисторов и других элементов. Оно необходимо для безопасного функционирования в нормальных и аварийных рабочих условиях.
— Заземление молниезащиты – молниеприемники и разрядники соединяются с землей, чтобы токи молнии отводились в землю без ущерба для электроустановки и находящихся рядом людей.
— Защитное заземление – металлические части, по которым не проходит ток, но есть риск оказаться под напряжением в случае замыкания на корпус. Для обеспечения безопасности соединяются с землей.
Нормальные величины для сопротивления заземляющих устройств
Согласно Правилам устройства электроустановок, оптимальная периодичность измерений сопротивления заземления – не реже, чем единожды в год. При этом первая проверка осуществляется сразу после монтажных работ, чтобы удостовериться, что схема заземлена правильно.
Норматив величины сопротивления заземления зависит от напряжения источника в цепи.
|
Трехфазный ток в источнике с напряжением: |
Однофазный ток в источнике с напряжением: |
Норма сопротивления заземления |
660 В |
380 В |
Не превышает 2 Ом |
|
380 В |
220 В |
Не превышает 4 Ом |
|
220 В |
127 В |
Не превышает 6 Ом |
Как измеряют сопротивление заземления
Методика измерения сопротивления заземляющих устройств основывается на разных теоретических базах:
- по формуле Дуайта (вычисляет сопротивление заземления в зависимости от радиуса электрода, глубины его погружения в землю и среднего удельного сопротивления грунта)
- по принципу падения потенциала
- по стандартному 3-проводному методу (другое название — метод 62%)
- по двухточечному методу (с последовательно включенными двумя устройствами заземления — методика, отлично подходящая для городских условий)
- по методу двух клещей (когда передающие клещи провоцируют ток в контуре, а дополнительные — снимают его величину)
- по методу Веннера (выявляет зависимость между расстоянием от электрода до электрода и глубиной, где течет ток).

Замер сопротивления контура заземления проходит с применением измерительных приборов М416 или Ф4103-М1. Ход работ таков:
- Элементы питания устанавливаются в измеритель заземления.
- Устанавливается переключатель в положение «Контроль», при этом стрелку индикатора нужно привести в отметку «0» после нажатия кнопки и вращения рукоятки «реохорд». Соединительные провода подключаются к прибору-измерителю, как указано в инструкции.
- Зонд и заземлитель (которые выступают в качестве вспомагательных электродов) углубляют до 0,5 м, затем подключают к ним соединительные провода.
- Переключатель устанавливают в «Х1», нажимают кнопку и двигают стрелку индикатора вращением ручки реохорда в нулевое положение. Результат умножается на необходимый множитель.
Методы замеров сопротивления заземляющих устройств
По 3-проводной схеме (3П) сопротивление заземляющего устройства измеряется при значениях выше 5 Ом. В остальных случаях прибор подключается по 4-проводной схеме (4П). Нужный метод измерения выбирается кнопкой «Режим». При использовании метода 4П выполняются следующие действия:

- Определяется максимальная диагональ (Д) заземляющего устройства (ЗУ).
- ЗУ соединяется измерительными кабелями с гнездами Т1 и П1.
- В грунт на дистанции 1,5 Д, но не менее 20 м от ЗУ, устанавливается потенциальный штырь П2.
- В грунт на расстоянии больше 3Д, но не меньше 40 м от ЗУ, устанавливается токовый штырь Т2.
- К разъему Т2 прибора подключается соединительный кабель.
- Проводится серия замеров. При этом потенциальный штырь П2 последовательно устанавливается в грунт на расстоянии 10, 20, …, 90% от дистанции до токового штыря Т2. При этом ЗУ и измерительные штыри обычно размещаются на одной линии. Амплитудное значение напряжения помехи (при его наличии) измеряется в вольтах и отображается на индикаторе. В таком случае нужно отыскать подходящее направление размещения штырей, чтобы минимизировать значение напряжения помехи.

- Строится график зависимости сопротивления от дистанции между ЗУ и П2. При равномерном возрастании сопротивления в средней части графика истинным считается значение между точками с наименьшей разницей величины сопротивления (не более 5%). Иначе все расстояния от ЗУ до П2 и Т2 нужно увеличить в 1,5–2 раза или сменить направление расположения штырей.
При использовании 3-проводного метода нужно выбрать его кнопкой «Режим», подсоединить измерительный кабель наименьшей длины к гнезду Т1. Замеры выполняются аналогично, но важно учесть, что измеренная величина сопротивления ЗУ включает сопротивление измерительного кабеля, подсоединенного к гнезду Т1.
Используемые приборы и средства
 Сопротивление ЗУ замеряется специальными приборами – измерителями сопротивления заземления типа ИС-10, EurotestXE 2,5 кВ MI 3102H, М416, Ф4103-М1, MRU различных конфигураций и др. Дополнительно используются диэлектрические боты и перчатки, защитная каска и инструмент с изолирующими рукоятками.
Сопротивление ЗУ замеряется специальными приборами – измерителями сопротивления заземления типа ИС-10, EurotestXE 2,5 кВ MI 3102H, М416, Ф4103-М1, MRU различных конфигураций и др. Дополнительно используются диэлектрические боты и перчатки, защитная каска и инструмент с изолирующими рукоятками.
В процессе проведения работ используется инструмент для забивания электродов в грунт на глубину не менее 0,5 м. Прибор подключается к корпусу электроустановки с помощью щупа, в роли которого применяется квадратный напильник с глухоприсоединенным медным проводом сечением 2,5 мм2.
Периодичность проведения замеров
Периодичность необходимых замеров сопротивления ЗУ основывается на правилах эксплуатации технических устройств. Для зданий действуют индивидуальные правила, включающие общие рекомендации по осмотру контура заземления. Периодичность замеров значится в специальных справочных материалах, используемых при реализации профилактических мероприятий. В большинстве случаев для поддержания работоспособности электросети достаточно осматривать участки заземления раз в полгода.
Замеры сопротивления переносного электрооборудования и дымовых труб должны проводиться ежегодно и включать обследование грунта возле заземленного электрооборудования. Сопротивление ЗУ в виде опор воздушных ЛЭП с напряжением до 1 кВт необходимо измерять с периодичностью раз в 6 лет, а с напряжением более 1 кВт – раз в 12 лет. Замеры сопротивления ЗУ нужно проводить во время максимальной засухи или замерзания грунта.
Инженерный центр «ПрофЭнергия» имеет огромный опыт и высокоточное оборудование, позволяющее оперативно измерять сопротивление заземляющих устройств и проводить другие электротехнические работы.
 Инженерный центр «ПрофЭнергия» имеет все необходимые лицензии для измерения сопротивления заземляющих устройств, слаженный коллектив профессионалов и сертификаты, которые дают право осуществлять все необходимые испытания и замеры. Оставив выбор на электролаборатории «ПрофЭнергия» вы выбираете надежную и качествунную работу своего оборудования!
Инженерный центр «ПрофЭнергия» имеет все необходимые лицензии для измерения сопротивления заземляющих устройств, слаженный коллектив профессионалов и сертификаты, которые дают право осуществлять все необходимые испытания и замеры. Оставив выбор на электролаборатории «ПрофЭнергия» вы выбираете надежную и качествунную работу своего оборудования!
Если Вы хотите заказать замер сопротивления заземления, а также по другим вопросам, звоните по телефону: +7 (495) 181-50-34.
90000 The most common methods of measuring the resistance of an earth electrode 90001 90002 Earth resistance of an earth electrode 90003 90004 When an earth electrode system has been designed and installed, it is usually necessary to measure and confirm the earth resistance between the electrode and «true Earth». The most commonly used method of measuring the earth resistance of an earth electrode is the 3-point measuring technique shown in Figure 1. 90005 90006 The most common methods of measuring the resistance of an earth electrode 90004 This method is derived from the 4-point method, which is used for soil resistivity measurements.90005 90004 The 3-point method, called the 90010 «fall of potential» method 90011, comprises the Earth Electrode to be measured and two other electrically independent test electrodes, usually labelled P (Potential) and C (Current). These test electrodes can be of lesser «quality» (higher earth resistance) but must be electrically independent of the electrode to be measured. 90005 90013 90013 Figure 1 — The 3-point Method of Earth Resistance Measurement 90004 An alternating current (I) is passed through the outer electrode C and the voltage is measured, by means of an inner electrode P, at some intermediary point between them.90005 90017 90004 The Earth Resistance is simply calculated using Ohm’s Law: 90010 Rg = V / I. 90011 90005 90022 90004 Other more complex methods, such as the Slope Method or the Four Pole Method, have been developed to overcome specific problems associated with this simpler procedure, mainly for measurements of the resistance of large earthing systems or at sites where space for locating the test electrodes is restricted. 90005 90004 Regardless of the measurement method employed, 90010 it should be remembered that the measurement of earth resistance is as much an art as it is a science 90011, and resistance measurements can be affected by many parameters, some of which may be difficult to quantify.As such, it is best to take a number of separate readings and average them, rather than rely on the results of a single measurement. 90005 90004 When performing a measurement, the aim is to position the auxiliary test electrode C far enough away from the earth electrode under test so that the auxiliary test electrode P will lie outside the effective resistance areas of both the earth system and the other test electrode ( see Figure 2). 90005 90031 90031 Figure 2 — Resistance areas and the variation of the measured resistance with voltage electrode position 90033 90034 90010 If the current test electrode, C, is too close 90011, the resistance areas will overlap and there will be a steep variation in the measured resistance as the voltage test electrode is moved.90037 90034 90010 If the current test electrode is correctly positioned 90011, there will be a ‘flat’ (or very nearly so) resistance area somewhere in between it and the earth system, and variations in the position of the voltage test electrode should only produce very minor changes in the resistance figure. 90037 90042 90004 The instrument is connected to the earth system under test via a short length of test cable, and a measurement is taken. 90005 Measurement accuracy can be affected 90010 by the proximity of other buried metal objects to the auxiliary test electrodes 90011.Objects such as fences and building structures, buried metal pipes or even other earthing systems can interfere with the measurement and introduce errors. 90004 Often it is difficult to judge, merely from visual inspection of the site, a suitable location for the tests stakes 90010 and so it is always advisable to perform more than one measurement to ensure the accuracy of the test 90011. 90005 90051 90052 Fall of Potential Method 90053 90004 This is one of the most common methods employed for the measurement of earth resistance and is best suited to small systems 90010 that do not cover a wide area 90011.It is simple to carry out and requires a minimal amount of calculation to obtain a result. 90005 90058 90058 Measuring earth resistance with fall of potential method (photo credit: eblogbd.com) 90004 90010 This method is generally not suited to large earthing installations 90011, as the stake separations needed to ensure an accurate measurement can be excessive, requiring the use of very long test leads (refer to Table 1). 90005 90004 Normally, the outer test electrode, or current test stake, is driven into the ground 30 to 50 metres away from the earth system, (although this distance will depend on the size of the system being tested — refer to Table 1) and the inner electrode, or voltage test stake, is then driven into the ground mid-way between the earth electrode and the current test stake, and in a direct line between them.90005 90004 90010 Table 1 90011 — Variation of current and voltage electrode separation with maximum earth system dimensions, in metres 90005 90070 90071 90072 90073 Maximum dimension across 90051 earth system 90075 90073 Distance from ‘electricalcentre’ 90051 of earth system to voltage test stake 90075 90073 Minimum distance from 90051 ‘electrical centre’ of earth system 90051 to current test stake 90075 90083 90072 90073 1 90075 90073 15 90 075 90073 30 90 075 90083 90072 90073 2 90075 90073 20 90 075 90073 40 90 075 90083 90072 90073 5 90075 90073 30 90 075 90073 60 90 075 90083 90072 90073 10 90 075 90073 43 90 075 90073 85 90 075 90083 90072 90073 20 90 075 90073 60 90 075 90073 120 90 075 90083 90072 90073 50 90 075 90073 100 90 075 90073 200 90 075 90083 90072 90073 100 90 075 90073 140 90 075 90073 280 90 075 90083 90140 90141 90004 The Fall of Potential method incorporates a check to ensure that 90010 the test electrodes are indeed positioned far enough away for a correct reading to be obtained 90011.It is advisable that this check be carried, as it is really the only way of ensuring a correct result. 90005 90004 90010 To perform a check on the resistance figure, two additional measurements should be made: 90011 90005 90150 90034 The first with the voltage test electrode (P) moved 10% of the original voltage electrode-to-earth system separation away from its initial position, and 90037 90034 The second with it moved a distance of 10% closer than its original position, as shown in Figure 3.90037 90155 90156 90156 Figure 3 — Checking the validity of a resistance measurement 90004 If these two additional measurements are in agreement with the original measurement, within the required level of accuracy, then the test stakes have been correctly positioned and the DC resistance figure can be obtained by averaging the three results. 90005 90004 However, 90010 if there is substantial disagreement amongst any of these results 90011, then it is likely that the stakes have been incorrectly positioned, either by being too close to the earth system being tested, too close to one another or too close to other structures that are interfering with the results.90005 90004 The stakes should be repositioned at a larger separation distance or in a different direction and the three measurements repeated. This process should be repeated until a satisfactory result is achieved. 90005 90051 90052 The 62% Method 90053 90004 The Fall of Potential method can be adapted slightly for use with medium sized earthing systems. This adaptation is often referred to as the 62% Method, 90010 as it involves positioning the inner test stake at 62% of the earth electrode-to-outer stake separation 90011 (recall that in the Fall-of-Potential method, this figure was 50%).90005 90004 All the other requirements of test stake location — that they be in a straight line and be positioned away from other structures — remain valid. 90005 90004 When using this method, it is also advisable to repeat the measurements with the inner test stake moved ± 10% of the earth electrode-inner test stake separation distance, as before. 90005 90004 90178 90179 90005 90004 The main disadvantage with this method is that the theory on which it is based relies on the assumption that the underlying soil is homogeneous, which in practice is rarely the case.Thus, care should be taken in its use and a soil resistivity survey should always be carried out. 90005 90004 90010 Alternatively, one of the other methods should be employed. 90011 90005 90051 90052 Other Test Methods 90053 90004 Many other methods exist for taking earth resistance measurements. Many of these methods have been designed in an attempt to alleviate the necessity for excessive electrode separations, when measuring large earth systems, or the requirement of having to know the electrical centre of the system.90005 90004 90010 Three such methods are briefly described below. 90011 Specific details are not given here, but instead the reader is referred to the relevant technical paper where these systems are described in detail. 90005 90150 90034 The slope method 90037 90034 The star-delta method 90037 90034 The four-potential method (Wenner method) 90037 90155 90051 90205 (a) The Slope Method 90206 90004 90010 This method is suitable for use with large earthing systems, such as power substation earths.90011 It involves taking a number of resistance measurements at various earth system to voltage electrode separations and then plotting a curve of the resistance variation between the earth and the current. 90005 90004 Using this method it is possible to calculate the theoretical optimum location for the voltage electrode and thus, from the resistance curve, calculate the true resistance. 90005 90004 The additional measurement and calculation effort tends to relegate this system to use with only very large or complex earthing systems.90005 90215 90215 Potential probe locations for using the slope method (figure credit: Whitham D. Reeve) 90004 For full details of this method, refer to paper 62975, written by Dr G.F. Tagg, taken from the proceedings of IEE volume 117, No 11, Nov. 1970. 90005 90004 90010 NETA WORLD TechTips ‘Slope Method’ by by Jeff Jowett AVO International: 90011 90005 90004 Download paper 90005 90051 90205 (b) The Star-Delta Method 90206 90004 This technique is well suited to use with large systems in built up areas or on rocky terrain, where it may be difficult to find suitable locations for the test electrodes, particularly over long distances in a straight line.90005 90004 90010 Three test electrodes, set up at the corners of an equilateral triangle with the earth system in the middle 90011, are used and measurements are made of the total resistance between adjacent electrodes, and also between each electrode and the earthing system. 90005 90004 Using these results, a number of calculations are performed and a result can be obtained for the resistance of the earth system. This method, developed by W. Hymers, is described in detail in Electrical Review, January тисяча дев’ятсот сімдесят п’ять.90005 90004 90010 NETA WORLD TechTips ‘Ground Testing in Difficult Installations’ by Jeffrey R. Jowett (Megger): 90011 90005 90004 Download paper 90005 90051 90205 (c) The Four Potential Method (Wenner method) 90206 90004 This technique, helps overcome some of the problems associated with the requirement 90010 for knowing the electrical centre of the earthing systems being tested 90011. 90005 90004 This method is similar in set up to the standard Fall of Potential method, 90010 except that a number of measurements are made with the voltage electrode at different positions 90011 and a set of equations are used to calculate the theoretical resistance of the system.90005 90004 The main draw back with the Four Potential method is that, like with the Fall of Potential method, it can require excessive electrode separation distances if the earthing system being measured is large. 90005 90004 90010 NETA WORLD TechTips ‘Ground Resistance Testing: Four Potential Method’ by Jeffrey R. Jowett (Megger): 90011 90005 90004 Download paper 90005 90004 90262 90010 Reference // 90011 Earthing Techniques by Lightning & Surge Technologies 90265 90005 .90000 The easiest way to measure ground resistance using clamp meter, but be carefull! 90001 90002 Why clamp meter / tester for grounding? 90003 90004 The ground clamp meter / tester is an effective and time-saving tool when used correctly 90005 because the user does not have to disconnect the ground system 90006 to make a measurement or place probes in the ground. 90007 90008 The easiest way to measure ground resistance using clamp meter (photo credit: Linemanchannel.com via Youtube) 90004 The method is based on Ohm’s Law, where: 90007 90004 90005 R (resistance) 90006 = V (voltage) / I (current) 90007 90004 The clamp includes a transmit coil, which applies the voltage and a receive coil, which measures the current.The instrument applies a known voltage to a complete circuit, measures the resulting current flow and calculates the resistance (see figure 1). 90007 90017 90017 Figure 1 — Clamp method for measuring ground resistance 90004 The clamp method requires a complete electrical circuit to measure. The operator has no probes and therefore can not set up the desired test circuit. The operator must be certain that earth is included in the return loop. The clamp tester measures the complete resistance of the path (loop) that the signal is taking.All elements of the loop are measured in series. 90007 90004 The method assumes that 90005 only the resistance of the ground electrode under test contributes significantly 90006. Based on the math behind the method (to be reviewed below), the more returns, the smaller the contribution of extraneous elements to the reading and, therefore, the greater the accuracy. 90007 90004 The major advantage of the clamp method is 90005 that it is quick and easy 90006. The ground electrode does not have to be disconnected from the system to take the measurement and no probes need to be driven and no cables connected.90007 90004 In addition, it includes the bonding and overall connection resistance. Good grounding must be complemented by «bonding», having a continuous low-impedance path to ground. Fall of potential measures only the ground electrode, not the bonding (leads must be shifted to make a bonding test). 90007 90004 Because the clamp uses the grounding conductor as part of the return, 90005 an «open» or high resistance bond 90006 will show up in the reading. 90007 90035 90035 Checking the ground resistance using clamp meter (on photo: Fluke earth / ground clamp meter; credit: Amazon) 90004 The clamp ground tester also allows the operator to measure the leakage current flowing through the system.If an electrode has to be disconnected, the instrument will show whether current is flowing to indicate whether it is safe to proceed. 90007 90004 Unfortunately, the clamp ground tester is often misused 90005 in applications where it will not give an effective reading 90006. The clamp method is effective only in situations where there are multiple grounds in parallel. It can not be used on 90005 isolated grounds as there is no return path 90006. 90007 90004 Therefore, it can not be used for installation checks or commissioning new sites.It also can not be used if an alternate lower resistance return exists not involving the soil 90005 (such as with cell towers) 90006. 90007 90004 Unlike with fall of potential testing, there is no way of proofing the result, meaning the results must be taken on «faith.» The clamp ground tester does fill a role as one tool that the technician could have in his «bag», but not the only tool. 90007 90051 90052 Clamp ground testing theory and methodology 90053 90004 Understanding how and why the clamp method works helps in understanding where it will and will not operate, and how to optimize its use.As mentioned, the clamp test method is based on Ohm’s Law (R = V / I). 90007 90004 Understanding Ohm’s law and how it applies to series and parallel circuits is the first step to understanding 90005 how and why a clamp ground tester works 90006. 90007 90004 90005 The following graphics will show and explain the following: 90006 90007 90064 90065 Series circuit, 90066 90065 Parallel circuit, 90066 90065 Parallel-series circuit and 90066 90065 The math used to determine the total current and resistance 90066 90073 90051 90075 Series Circuit 90076 90077 90077 Figure 2 — Determining the total current and resistance with series circuit 90004 In a series circuit (figure 2), total current and total resistance are calculated as follows: 90007 90004 90005 I 90083 t 90084 90006 = I 90083 1 90084 = I 90083 2 90084 = I 90083 3 90084 90051 90005 R 90083 t 90084 90006 = R 90083 1 90084 + R 90083 2 90084 + R 90083 3 90084 90007 90051 90075 Parallel Circuit 90076 90107 90107 Figure 3 — Determining the total current and resistance with parallel circuit 90004 In a parallel circuit (figure 3), total current and total resistance are calculated as follows: 90007 90004 90005 I 90083 t 90084 90006 = I 90083 1 90084 + I 90083 2 90084 + I 90083 3 90084 90051 90005 R 90083 t 90084 90006 = 1 / (1 / R 90083 1 90084 + 1 / R 90083 2 90084 + 1 / R 90083 3 90084) 90007 90051 90075 Parallel-Series Circuit 90076 90137 90137 Figure 4 — Determining the total current and resistance with parallel-series circuit 90004 In a parallel-series circuit (figure 4), total current and total resistance are calculated as follows: 90007 90004 90005 I 90083 t 90084 90006 = I 90083 1 90084 + I 90083 2 90084 = I 90083 3 90084 = I 90083 4 90084 + I 90083 5 90084 90051 90005 R 90083 t 90084 90006 = 1 / (1 / R 90083 1 90084 + 1 / R 90083 2 90084) + 1 / (1 / R 90083 3 90084 + 1 / R 90083 4 90084) 90007 90051 90052 Clamp Test Methodology 90053 90004 The head of a clamp ground tester includes two cores (see figure 5).One core 90005 induces a test current 90006 and the other measures 90005 how much was induced 90006. The input or primary voltage of the test current inducing core is kept constant, so the current actually induced into the test circuit is directly proportional to the loop resistance. 90007 90179 90179 Figure 5 — Clamp Test Methodology 90004 The important thing to remember with clamp testing is that clamp ground testers effectively make loop resistance measurements. Clamp measurements are 90005 loop measurements 90006.For the clamp method to work there must be a series- parallel resistance path (90184 and the lower the better 90185). 90007 90004 The more electrodes or ground paths in the system the nearer the measurement gets to the actual electrode 90005 under test’s true resistance 90006. 90007 90004 The following figure shows 90005 a pole ground configuration 90006, one of the most effective applications of the clamp ground tester. 90007 90195 90195 Figure 6 — Pole ground configuration 90004 The circuit diagram for this configuration follows (90005 based on a clamp ground tester being clamped around pole 6 90006): 90007 90201 90201 Figure 7 — Circuit diagram for above configuration based on a clamp ground tester being clamped around pole 6 90004 The clamp ground tester is clamped around one of the electrodes and then measures the resistance of the entire loop.The remaining ground electrodes are all in parallel, and, as a group, are in series with the ground electrode being measured. 90005 If the clamp tester is clamped around pole # 6 90006, the measurement of the resistance of the entire loop would be calculated using the following equation: 90007 90004 R 90083 loop 90084 = R 90083 6 90084 + (1 / (1 / R 90083 1 90084 + 1 / R 90083 2 90084 + 1 / R 90083 3 90084 + 1 / R 90083 4 90084 + 1 / R 90083 5 90084) ) 90007 90004 For six similar ground electrodes with a resistance of 90005 10 Ω each 90006, the measurement of the total loop resistance would be: 90007 90004 R 90083 loop 90084 = 10 + (1 / (1/10 + 1/10 + 1/10 + 1/10 + 1/10)) 90051 R 90083 loop 90084 = 10 + (1 / (5/10)) 90051 R 90083 loop 90084 = 10 + 2 90007 90004 90005 R 90083 loop 90084 = 12 Ω 90006 90007 90004 The measurement of the loop resistance is relatively close to the resistance of the ground electrode being tested.If there were 60 similar ground electrodes with a resistance of 90005 10 Ω each 90006, the measurement of the total loop resistance would be: 90007 90004 90005 R 90083 loop 90084 90006 = 10 Ω + 0.17 Ω = 10.17 Ω 90007 90004 The more ground electrodes in parallel, the smaller the impact of the resistance of the electrodes not being tested and the closer the loop resistance is to the resistance of the electrode being tested. 90005 If the electrode being measured has a high resistance, the test will indicate that there is a problem.90006 90007 90004 Using the six electrode example, if electrode number 6 had a resistance of 90005 100 Ω 90006 and all the other electrodes had resistances of 90005 10 Ω 90006, the measurement of the loop resistance would be: 90007 90004 R 90083 loop 90084 = 100 + (1 / (1/10 + 1/10 + 1/10 + 1/10 + 1/10)) 90051 R 90083 loop 90084 = 100 + (1 / (5/10)) 90051 R 90083 loop 90084 = 100 + 2 90007 90004 90005 R 90083 loop 90084 = 102 Ω 90006 90007 90004 In the following example, the clamp ground tester would indicate the bad ground.If the 90005 100 Ω 90006 electrode was one of the electrodes not being measured, the impact on the overall measurement would be minimal: 90007 90004 R 90083 loop 90084 = 10 + (1 / (1/10 + 1/100 + 1/10 + 1/10 + 1/10)) 90051 R 90083 loop 90084 = 10 + (1 / (41/100)) 90051 R 90083 loop 90084 = 10 + 2.44 90007 90004 90005 R 90083 loop 90084 = 12.44 Ω 90006 90007 90004 90005 NOTE // 90006 Please note that the measured resistance will always be higher than the actual resistance of the ground electrode being tested.Any error present is on the side of safety, as resistance guidelines are for maximum ground resistance. 90007 90303 90004 This means that if 90005 the measured resistance is below target level for the ground electrode 90006, the operator can be assured that actual resistance will also be below the target. 90007 90308 90051 90052 To conclude // 90053 90004 In summary, remember that a clamp ground tester measurement is a 90005 measurement of the resistance of the entire loop 90006. There must be a loop resistance to measure.If there is not a loop to measure the operator can create one with a temporary jumper lead. The greater the number of parallel paths, the closer the measured value will be to the actual earth resistance of the electrode under test. 90007 90004 The clamp ground tester 90005 can easily indicate a poor electrode 90006 whether there are a few parallel paths in series with the measured value, or many parallel paths present. 90007 90004 Remember that the earth path must be in the circuit to measure ground resistance.This caveat sounds obvious, but if you have metal structures involved there may be a connection through that, rather than the earth mass. 90007 90051 90052 Examples of measuring ground rod resistance using clamp meter 90053 90004 90326 90327 90007 90004 90330 90327 90007 90004 90184 90005 Reference // 90006 Guide to Clamp Ground Testing by MEGGER 90185 90007 .90000 90001 90002% PDF-1.4 % 506 0 obj > endobj xref 506 86 0000000016 00000 n 0000003447 00000 n 0000003580 00000 n 0000004627 00000 n 0000004769 00000 n 0000004796 00000 n 0000005105 00000 n 0000005219 00000 n 0000008295 00000 n 0000010601 00000 n 0000010753 00000 n 0000011299 00000 n 0000011779 00000 n 0000012056 00000 n 0000012630 00000 n 0000012657 00000 n 0000012978 00000 n 0000013253 00000 n 0000013803 00000 n 0000016706 00000 n 0000020139 00000 n 0000023720 00000 n 0000026323 00000 n 0000026957 00000 n 0000027390 00000 n 0000027477 00000 n 0000027705 00000 n 0000028396 00000 n 0000028621 00000 n 0000029128 00000 n 0000030994 00000 n 0000033698 00000 n 0000047570 00000 n 0000047683 00000 n 0000047753 00000 n 0000047841 00000 n 0000048029 00000 n 0000053674 00000 n 0000053744 00000 n 0000053829 00000 n 0000057192 00000 n 0000057465 00000 n 0000057638 00000 n 0000057927 00000 n 0000060933 00000 n 0000061011 00000 n 0000061090 00000 n 0000061187 00000 n 0000061336 00000 n 0000061660 00000 n 0000061715 00000 n 0000061831 00000 n 0000061909 00000 n 0000062235 00000 n 0000062290 00000 n 0000062406 00000 n 0000062484 00000 n 0000062809 00000 n 0000062864 00000 n 0000062980 00000 n 0000063058 00000 n 0000063383 00000 n 0000063438 00000 n 0000063554 00000 n 0000070184 00000 n 0000070223 00000 n 0000103038 00000 n 0000103077 00000 n 0000113173 00000 n 0000113212 00000 n 0000185440 00000 n 0000185518 00000 n 0000253801 00000 n 0000254256 00000 n 0000254334 00000 n 0000366320 00000 n 0000366769 00000 n 0000366847 00000 n 0000457123 00000 n 0000457574 00000 n 0000457652 00000 n 0000548085 00000 n 0000548533 00000 n 0000552009 00000 n 0000684266 00000 n 0000002016 00000 n trailer ] / Prev 3530785 >> startxref 0 %% EOF 591 0 obj > stream h ެ UmLSg> m — ի C.\ +] RhA, (ȥ @ ~ MqN7t [b \ 4Y2-̒-sjdv {f ٟ y: 90003.90000 Ground Resistance Measurements ~ Electrical Knowhow 90001 90002 In Article «90003 Ground Resistance Calculations 90004», I explained the following points: 90002 90006 90007 Calculating Ground Resistance, 90008 90007 Calculating Ground Resistance for substations, 90008 90007 Verifying Ground Grid Conductor Installation, 90008 90007 Design Guidelines and Requirements. 90008 90015 90016 Also, In Article «90017 90003 Introduction to Earthing System 90004», I explained the following points: 90002 90002 90006 90007 Introduction, 90008 90007 Determining Ground Resistance, 90008 90007 Soil Resistivity.90008 90015 90002 Today, I will explain the Ground Resistance Measurements. 90016 90003 90033 Ground Resistance Measurement 90034 90004 90017 90002 90003 90033 90002 90034 90004 90003 90033 90002 90034 90004 90002 A careful measurement of the resistance of the ground installation as constructed is desirable. Extreme precision is not always possible in measurement, but the results should be more dependable than values calculated by design engineering. 90002 90050 90051 90052 90053 90003 Instruments Used For Ground Resistance Measurements 90004 These are some of the instruments used for ground resistance measurements: 90006 90007 Direct-indicating megohmmeter with self-contained hand- or power-driven internal generator, 90008 90015 90006 90007 Direct- indicating megohmmeter with self-contained battery, 90008 90015 90006 90007 Direct-indicating megohmmeter with a rectifier using an external alternating-current supply, 90008 90015 90006 90007 Resistance Bridge with a galvanometer and batteries.90008 90015 90002 90073 90074 90075 90076 90050 90051 90052 90053 90003 Ground Impedance Measurement Methods 90004 There are many Ground Impedance Measurement Methods as follows: 90083 90006 90007 The 2-Point Method, 90008 90007 The 3-Point Method, 90008 90007 The Fall of Potential Method, 90008 90007 The 62% Rule, 90008 90007 The Ratio Method, 90008 90007 The Tag Slope Method, 90008 90007 The Intersecting Curve Method, 90008 90007 Staged Fault Tests, 90008 90007 Driving Point Impedance, 90008 90007 The SGM Method.90008 90015 90016 But, There are four basic methods of measuring ground resistance: 90017 90006 90007 Fall-of-Potential Method, 90008 90007 Two-Point Method, 90008 90007 Three-Point Method, 90008 90007 Ratio Method. 90008 90015 90002 In this ground inspection course, I will explain only the most used method for Ground Impedance Measurement which is the Fall-of-Potential Method. 90002 90073 90074 90075 90076 90003 90033 90002 Fall-of-Potential Method 90034 90004 90050 90051 90052 90053 90003 Uses for Fall-of-Potential Method 90004 Use the Fall-of-Potential Slope Method for determining the resistance of large areas such as substation yards , ground perimeters of large buildings, and other large areas.90003 Figure 1 90004 shows the measurement arrangement for this method of testing. 90073 90074 90075 90076 90141 90051 90052 90144 90073 90074 90052 90144 90003 Figure 1. Fall-of-Potential method for ground resistance measure 90004 90073 90074 90075 90076 90050 90051 90052 90053 90003 The Measurement Arrangement for Fall-of-Potential Method 90004 1 Place the current probe (cp) a minimum of 328 feet (100 meters) from the ground grid boundaries. On large size plants or substations this distance (c), is longer.The formula for this distance is: grid, grounding system, or substation diagonal of the area in meters (DL) equals the square root of one of the sides squared (a2) plus the other side squared (b2) or 90016 90017 2 Insert the (cp) probe into the earth a minimum of 2 feet (0.6 m) in depth.3- Insert the potential probe (pp) into the earth in a straight line with the CP at distance (p) from the ground grid (g ) you are measuring. 4 A minimum of 3 different measurements at 3 different distances must be recorded.They are equal to 0.2C, 0.4C, and 0.6C and are represented as R1, R2, and R3 respectively as in Figure 2. 90141 90051 90052 90144 90073 90074 90052 90144 90003 Figure 2. Resistance values related to distance 90004 90073 90074 90075 90076 Pass a test current through the ground grid through the cp. The pp measures the 90177 voltage 90178 produced between the ground grid and the surface of the ground. The instrument directly measures the resistance (R) of the ground grid by dividing the measured voltage by the test current (E / I).90016 5 Calculate the slope variation coefficient using the following formula: 90017 90003 90177 μ 90178 90004 is a measure of the change of the slope in the resistance curve.μ should be less than or equal to 1.59 (90177 μ 90178 90177 90178 ≤ 1.59 ). If 90177 μ 90178 is not less than or equal to 1.59, do the whole measuring process again with a longer (C) distance.6- Include the key plans of the location, the weather, and soil conditions when filling out your report. 90073 90074 90075 90076 90050 90051 90052 90053 90003 Interpretation of the Result 90004 1 Obtain the value, pt / c, from the table of values in 90003 Figure 3 90004, once you calculate the slope variation coefficient 90177 μ.90178 90177 2 90178 pt is the distance of the potential probe position to the ground grid where the true resistance value should be measured. 3 Measure the true resistance by inserting the potential probe at the corresponding distance pt. Take an average value of the measured true resistances from at least three different compass directions from the grid. This result is the ground resistance of the grid. 90073 90074 90075 90076 90211 90051 90052 90214 90003 VALUES OF PT / C FOR VARIOUS VALUES OF (90177 μ 90178) 90004 90073 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 9022 2 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90052 90222 90222 90222 90222 90222 90222 90074 90075 90076 90003 Figure 3.Table of values for PT / C related to 90177 μ 90178 90004 90002 90016 90003 90033 Example # 1: 90034 90004 90017 90002 90002 Plot the measured resistance values against the potential probe spacing found from the curve in 90003 Figure 4 90004. 90141 90051 90052 90144 90073 90074 90052 90144 90003 Figure 4. Plotted resistance values 90004 90073 90074 90075 90076 90002 Calculate for μ using the resistance values below. Use the slope variation coefficient formula shown below also.90002 90002 90016 From Figure 3 for μ = 0.96; pt / C = 0.550 90017 90016 Measure the true resistance by positioning the potential probe at a distance equal to pt or 0.550 (C), or from Figure 4, pt = 0.550 (100m) = 55 m. 90017 90002 90002 90002 90002 90050 90051 90052 90053 90003 Factors Affecting Ground Impedance Measurement 90004 90002 90006 90007 Difficulty reaching true remote earth reference voltage, 90008 90007 Effect of Auxiliary Electrode Location (Earth Current Return), 90008 90007 Size and location of voltage probes, 90008 90007 Interaction Between Instrumentation Wires, 90008 90007 Interference from Overhead Lines and their Grounding, 90008 90007 Background 60 Hz Voltage and Harmonics, 90008 90007 Ground Impedance Magnitude.90008 90015 These factors will be discussed in the next Article. 90073 90074 90075 90076 90016 In the next Article, I will explain 90003 the Factors affecting Ground Resistance Measurement Reliability 90004. Please, keep following. 90017 .
