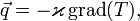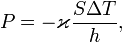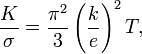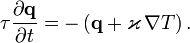+7 (919) 994-41-63 
E-mail:
Адрес: 105678, г. Москва, Шоссе Энтузиастов, д. 55 (Карта проезда)
Время работы: ПН-ПТ: с 9.00 до 18.00, СБ: с 9.00 до 14.00

Теплопроводность измеряется в: Теплопроводность — Википедия

Содержание

Теплопроводность — Википедия

Теплопрово́дность — способность материальных тел проводить энергию (теплоту) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.

Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В Международной системе единиц (СИ) единицей измерения коэффициента теплопроводности является Вт/(м·K).

Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.

Закон теплопроводности Фурье

В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:

q → = − ϰ g r a d ( T ) , {\displaystyle {\vec {q}}=-\varkappa \,\mathrm {grad} (T),}

где q → {\displaystyle {\vec {q}}}  — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, ϰ {\displaystyle \varkappa }  —

коэффициент теплопроводности (удельная теплопроводность), T {\displaystyle T}  — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору g r a d ( T ) {\displaystyle \mathrm {grad} (T)} (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

P = − ϰ S Δ T l , {\displaystyle P=-\varkappa {\frac {S\Delta T}{l}},} [Вт/(м·К) · (м2·К)/м = Вт/(м·К) · (м·К) = Вт]

где P {\displaystyle P}  — полная мощность тепловых потерь, S {\displaystyle S}  — площадь сечения параллелепипеда, Δ T {\displaystyle \Delta T}  — перепад температур граней, l {\displaystyle l}  — длина параллелепипеда, то есть расстояние между гранями.

Связь с электропроводностью

Связь коэффициента теплопроводности ϰ {\displaystyle \varkappa } с удельной электрической проводимостью σ {\displaystyle \sigma } в металлах устанавливает закон Видемана — Франца:

ϰ σ = π 2 3 ( k e ) 2 T , {\displaystyle {\frac {\varkappa }{\sigma }}={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}T,}
где k {\displaystyle k}  — постоянная Больцмана;
e {\displaystyle e}  — заряд электрона;
T {\displaystyle T}  — абсолютная температура.

Коэффициент теплопроводности газов

В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]

ϰ ∼ 1 3 ρ c v λ v ¯ , {\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}\lambda {\bar {v}},}

где ρ {\displaystyle \rho }  — плотность газа, c v {\displaystyle c_{v}}  — удельная теплоёмкость при постоянном объёме, λ {\displaystyle \lambda }  — средняя длина свободного пробега молекул газа, v ¯ {\displaystyle {\bar {v}}}  — средняя тепловая скорость. Эта же формула может быть записана как[3]

ϰ = i k 3 π 3 / 2 d 2 R T μ , {\displaystyle \varkappa ={\frac {ik}{3\pi ^{3/2}d^{2}}}{\sqrt {\frac {RT}{\mu }}},}

где i {\displaystyle i}  — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i = 5 {\displaystyle i=5} , для одноатомного i = 3 {\displaystyle i=3} ), k {\displaystyle k}  — постоянная Больцмана, μ {\displaystyle \mu }  — молярная масса, T {\displaystyle T}  — абсолютная температура, d {\displaystyle d}  — эффективный (газокинетический) диаметр молекул, R {\displaystyle R}  — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).

Теплопроводность в сильно разреженных газах

Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): ϰ ∼ 1 3 ρ c v l v ¯ ∝ P {\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}l{\bar {v}}\propto P} , где l {\displaystyle l}  — размер сосуда, P {\displaystyle P}  — давление.

Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.

Обобщения закона Фурье

Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл[4], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[5]

τ ∂ q ∂ t = − ( q + ϰ ∇ T ) . {\displaystyle \tau {\frac {\partial \mathbf {q} }{\partial t}}=-\left(\mathbf {q} +\varkappa \,\nabla T\right).}

Если время релаксации τ {\displaystyle \tau } пренебрежимо мало, то это уравнение переходит в закон Фурье.

Коэффициенты теплопроводности различных веществ

\tau
МатериалТеплопроводность, Вт/(м·K)
Графен4840 ± 440 — 5300 ± 480
Алмаз1001—2600
Графит278,4—2435
Арсенид бора[en]200—2000
Карбид кремния490
Серебро430
Медь401
Оксид бериллия370
Золото320
Алюминий202—236
Нитрид алюминия200
Нитрид бора180
Кремний150
Латунь97—111
Хром107
Железо92
Платина70
Олово67
Оксид цинка54
Сталь нелегированная47—58
Свинец35,3
Сталь нержавеющая (аустенитная) [6]15
Кварц8
Термопасты высокого качества5—6
Гранит2,4
Бетон сплошной1,75
Бетон на гравии или щебне из природного камня1,51
Базальт1,3
Стекло1—1,15
Термопаста КПТ-80,7
Бетон на песке0,7
Вода при нормальных условиях0,6
Кирпич строительный0,2—0,7
Силиконовое масло0,16
Пенобетон 0,05—0,3
Газобетон0,1—0,3
Древесина0,15
Нефтяные масла0,12
Свежий снег0,10—0,15
Пенополистирол (горючесть Г1)0,038—0,052
Экструдированный пенополистирол (горючесть Г3 и Г4)0,029—0,032
Стекловата0,032—0,041
Каменная вата0,034—0,039
Воздух (300 K, 100 кПа)0,022
Аэрогель0,017
Аргон (273—320 K, 100 кПа)0,017
Аргон (240—273 K, 100 кПа)0,015
Вакуум (абсолютный)0 (строго)

Также нужно учитывать передачу тепла из-за конвекции молекул и излучения. Например, при полной нетеплопроводности вакуума, тепловая энергия передаётся излучением (Солнце, инфракрасные теплогенераторы). В газах и жидкостях происходит перемешивание разнотемпературных слоёв естественным путём или искусственно (примеры принудительного перемешивания — фены, естественного — электрочайники). Также в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепловой энергии, даже если зазоры представляют собой идеальный вакуум.

Примечания

См. также

Ссылки

Теплопроводность — это… Что такое Теплопроводность?

Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела ( атомами, молекулами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Численная характеристика теплопроводности материала равна количеству теплоты, проходящей через материал площадью 1 кв.м за единицу времени (секунду) при единичном температурном градиенте. Данная численная характеристика используется для расчета теплопроводности для калибрования и охлаждения профильных изделий.

Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением объектов занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.

Закон теплопроводности Фурье

В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:

где  — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси,  — коэффициент теплопроводности (иногда называемый просто теплопроводностью),  — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

где  — полная мощность тепловых потерь,  — площадь сечения параллелепипеда,  — перепад температур граней,  — длина параллелепипеда, то есть расстояние между гранями.

Коэффициент теплопроводности измеряется в Вт/(м·K).

Коэффициент теплопроводности вакуума

Коэффициент теплопроводности вакуума почти ноль (чем глубже вакуум, тем ближе к нулю). Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, тепло в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.

Связь с электропроводностью

Связь коэффициента теплопроводности с удельной электрической проводимостью в металлах устанавливает закон Видемана — Франца:

где  — постоянная Больцмана,  — заряд электрона.

Коэффициент теплопроводности газов

Коэффициент теплопроводности газов определяется формулой[2]

Где: i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, M — молярная масса, T — абсолютная температура, d — эффективный диаметр молекул, R — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из не радиоактивных газов — у ксенона).

Обобщения закона Фурье

Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т.п. Инерционность в уравнения переноса первым ввел Максвелл[3], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[4]

Если время релаксации пренебрежимо мало, то это уравнение переходит в закон Фурье.

Коэффициенты теплопроводности различных веществ

\tau
МатериалТеплопроводность, Вт/(м·K)
Графен(4840±440) — (5300±480)
Алмаз1001—2600
Графит278,4—2435
Карбид кремния490
Серебро430
Медь382—390
Оксид бериллия370
Золото320
Алюминий202—236
Нитрид алюминия200
Нитрид бора180
Кремний150
Латунь97—111
Хром93,7
Железо92
Платина70
Олово67
Оксид цинка54
Сталь47
Кварц8
Стекло1-1,15
КПТ-80,7
Вода при нормальных условиях0,6
Кирпич строительный0,2—0,7
Силиконовое масло0,16
Пенобетон0,14—0,3
Древесина0,15
Нефтяные масла0,12
Свежий снег0,10—0,15
Вата0,055
Воздух (300 K, 100 кПа)0,026
Вакуум (абсолютный)0 (строго)

другие вещества

МатериалТеплопроводность, Вт/(м·K)
Кальций201
Бериллий201
Вольфрам173
Магний156
Родий150
Иридий147
Молибден138
Рутений117
Хром93,9
Осмий87,6
Титан21,9
Тефлон0,25
Бумага0,14
Полистирол0,082
Шерсть0,05
Минеральная вата0,045
Пенополистирол0,04
Стекловолокно0,036
Пробковое дерево0,035
Пеноизол0,035
Каучук вспененный0,03
Аргон0,0177
Аэрогель0,017
Ксенон0,0057

На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы). Так же в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепла, даже если зазоры представляют собой идеальный вакуум.

Примечания

См. также

Ссылки

Коэффициент теплопроводности — это… Что такое Коэффициент теплопроводности?

Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.

В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:

\vec{q}=-\varkappa\,\mathrm{grad}(T),

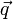где \vec{q} — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, 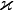\varkappa — коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Это выражение известно как закон теплопроводности Фурье.

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

P=-\varkappa\frac{S\Delta T}{h},

где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT — перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями.

Коэффициент теплопроводности измеряется в Вт/(м·K).

Коэффициенты теплопроводности различных веществ

МатериалТеплопроводность, Вт/(м·K)
Алмаз1001—2600
Серебро430
Медь382—390
Золото320
Алюминий202—236
Латунь97—111
Железо92
Платина70
Олово67
Сталь47
Кварц8
Стекло1
Вода0,6
Кирпич строительный0,2—0,7
Пенобетон0,14—0,3
Газобетон0,1—0,3
Дерево0,15
Шерсть0,05
Минеральная вата0,045
Пенополистирол0,04
Пеноизол0,035
Воздух (300 K, 100 кПа)0,026
Воздух (сухой неподвижный)0,024—0,031
Аргон0,0177
Ксенон0,0057
Аэрогель0,003
Вакуум (абсолютный)0 (строго)

На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).

Коэффициент теплопроводности вакуума

Коэффициент теплопроводности вакуума стремится к нулю. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тепло в вакууме передаётся только излучением. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают.

Связь с электропроводностью

Связь коэффициента теплопроводности K с удельной электрической проводимостью σ в металлах устанавливает закон Видемана — Франца:

\frac{K}{\sigma}=\frac{\pi^2}{3}\left(\frac{k}{e}\right)^2T,

где k — постоянная Больцмана, e — заряд электрона.

Обобщения закона Фурье

Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. д. Инерционность в уравнения переноса первым ввел Максвелл[1], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[2]

\tau\frac{\partial\mathbf{q}}{\partial t}=-\left(\mathbf{q}+\varkappa\,\nabla T\right).

Если время релаксации τ пренебрежимо мало, то это уравнение переходит в закон Фурье.

Примечания

  1. ↑ J. C. Maxwell, Philos. Trans. Roy. Soc. London 157 (1867) 49.
  2. ↑ C. Cattaneo, Atti Seminario Univ. Modena 3 (1948) 33.

См. также

Другие способы теплопередачи

Wikimedia Foundation. 2010.

Теплопроводность — Википедия

Теплопрово́дность — способность материальных тел проводить энергию (теплоту) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.

Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В Международной системе единиц (СИ) единицей измерения коэффициента теплопроводности является Вт/(м·K).

Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.

Закон теплопроводности Фурье

В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:

q → = − ϰ g r a d ( T ) , {\displaystyle {\vec {q}}=-\varkappa \,\mathrm {grad} (T),}

где q → {\displaystyle {\vec {q}}}  — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, ϰ {\displaystyle \varkappa }  — коэффициент теплопроводности (удельная теплопроводность), T {\displaystyle T}  — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору g r a d ( T ) {\displaystyle \mathrm {grad} (T)} (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

P = − ϰ S Δ T l , {\displaystyle P=-\varkappa {\frac {S\Delta T}{l}},} [Вт/(м·К) · (м2·К)/м = Вт/(м·К) · (м·К) = Вт]

где P {\displaystyle P}  — полная мощность тепловых потерь, S {\displaystyle S}  — площадь сечения параллелепипеда, Δ T {\displaystyle \Delta T}  — перепад температур граней, l {\displaystyle l}  — длина параллелепипеда, то есть расстояние между гранями.

Связь с электропроводностью

Связь коэффициента теплопроводности ϰ {\displaystyle \varkappa } с удельной электрической проводимостью σ {\displaystyle \sigma } в металлах устанавливает закон Видемана — Франца:

ϰ σ = π 2 3 ( k e ) 2 T , {\displaystyle {\frac {\varkappa }{\sigma }}={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}T,}
где k {\displaystyle k}  — постоянная Больцмана;
e {\displaystyle e}  — заряд электрона;
T {\displaystyle T}  — абсолютная температура.

Коэффициент теплопроводности газов

В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]

ϰ ∼ 1 3 ρ c v λ v ¯ , {\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}\lambda {\bar {v}},}

где ρ {\displaystyle \rho }  — плотность газа, c v {\displaystyle c_{v}}  — удельная теплоёмкость при постоянном объёме, λ {\displaystyle \lambda }  — средняя длина свободного пробега молекул газа, v ¯ {\displaystyle {\bar {v}}}  — средняя тепловая скорость. Эта же формула может быть записана как[3]

ϰ = i k 3 π 3 / 2 d 2 R T μ , {\displaystyle \varkappa ={\frac {ik}{3\pi ^{3/2}d^{2}}}{\sqrt {\frac {RT}{\mu }}},}

где i {\displaystyle i}  — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i = 5 {\displaystyle i=5} , для одноатомного i = 3 {\displaystyle i=3} ), k {\displaystyle k}  — постоянная Больцмана, μ {\displaystyle \mu }  — молярная масса, T {\displaystyle T}  — абсолютная температура, d {\displaystyle d}  — эффективный (газокинетический) диаметр молекул, R {\displaystyle R}  — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).

Теплопроводность в сильно разреженных газах

Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): ϰ ∼ 1 3 ρ c v l v ¯ ∝ P {\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}l{\bar {v}}\propto P} , где l {\displaystyle l}  — размер сосуда, P {\displaystyle P}  — давление.

Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.

Обобщения закона Фурье

Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл[4], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[5]

τ ∂ q ∂ t = − ( q + ϰ ∇ T ) . {\displaystyle \tau {\frac {\partial \mathbf {q} }{\partial t}}=-\left(\mathbf {q} +\varkappa \,\nabla T\right).}

Если время релаксации τ {\displaystyle \tau } пренебрежимо мало, то это уравнение переходит в закон Фурье.

Коэффициенты теплопроводности различных веществ

\tau
МатериалТеплопроводность, Вт/(м·K)
Графен4840 ± 440 — 5300 ± 480
Алмаз1001—2600
Графит278,4—2435
Арсенид бора[en]200—2000
Карбид кремния490
Серебро430
Медь401
Оксид бериллия370
Золото320
Алюминий202—236
Нитрид алюминия200
Нитрид бора180
Кремний150
Латунь97—111
Хром107
Железо92
Платина70
Олово67
Оксид цинка54
Сталь нелегированная47—58
Свинец35,3
Сталь нержавеющая (аустенитная) [6]15
Кварц8
Термопасты высокого качества5—6
Гранит2,4
Бетон сплошной1,75
Бетон на гравии или щебне из природного камня1,51
Базальт1,3
Стекло1—1,15
Термопаста КПТ-80,7
Бетон на песке0,7
Вода при нормальных условиях0,6
Кирпич строительный0,2—0,7
Силиконовое масло0,16
Пенобетон0,05—0,3
Газобетон0,1—0,3
Древесина0,15
Нефтяные масла0,12
Свежий снег0,10—0,15
Пенополистирол (горючесть Г1)0,038—0,052
Экструдированный пенополистирол (горючесть Г3 и Г4)0,029—0,032
Стекловата0,032—0,041
Каменная вата0,034—0,039
Воздух (300 K, 100 кПа)0,022
Аэрогель0,017
Аргон (273—320 K, 100 кПа)0,017
Аргон (240—273 K, 100 кПа)0,015
Вакуум (абсолютный)0 (строго)

Также нужно учитывать передачу тепла из-за конвекции молекул и излучения. Например, при полной нетеплопроводности вакуума, тепловая энергия передаётся излучением (Солнце, инфракрасные теплогенераторы). В газах и жидкостях происходит перемешивание разнотемпературных слоёв естественным путём или искусственно (примеры принудительного перемешивания — фены, естественного — электрочайники). Также в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепловой энергии, даже если зазоры представляют собой идеальный вакуум.

Примечания

См. также

Ссылки

Что такое теплопроводность и коэффициент теплопроводности. |

Теплопроводность.

Так что же такое теплопроводность? С точки зрения физики теплопроводность – это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).

Можно сказать проще, теплопроводность – это  способность материала проводить тепло. Если внутри тела имеется разность температур, то тепловая энергия переходит от более горячей его части к более холодной. Передача тепла происходит за счет передачи энергии при столкновении молекул вещества. Происходит это до тех пор, пока температура внутри тела не станет одинаковой. Такой процесс может происходить в твердых, жидких и газообразных веществах.

На практике, например в строительстве при теплоизоляции зданий, рассматривается другой аспект теплопроводности, связанный с передачей тепловой энергии. В качестве примера возьмем “абстрактный дом”. В “абстрактном доме” стоит нагреватель, который поддерживает внутри дома постоянную температуру, скажем, 25 °С. На улице температура тоже постоянная, например, 0 °С. Вполне понятно, что если выключить обогреватель, то через некоторое время в доме тоже будет 0 °С. Все тепло (тепловая энергия) через стены уйдет на улицу.

Чтобы поддерживать температуру в доме 25 °С, нагреватель должен  постоянно работать. Нагреватель постоянно создает тепло, которое постоянно уходит через стены на улицу.

 

Коэффициент теплопроводности.

Количество тепла, которое проходит через стены (а по научному – интенсивность теплопередачи за счет теплопроводности) зависит от разности температур (в доме и на улице), от площади стен и теплопроводности материала, из которого сделаны эти стены.

Для количественной оценки теплопроводности существует коэффициент теплопроводности материалов. Этот коэффициент отражает свойство вещества проводить тепловую энергию. Чем больше значение коэффициента теплопроводности материала, тем лучше он проводит тепло. Если мы собираемся утеплять дом, то надо выбирать материалы с небольшим значением этого коэффициента. Чем он меньше, тем лучше. Сейчас  в качестве материалов для утепления зданий  наибольшее распространение получили утеплители из минеральной ваты, и различных пенопластов. Набирает популярность новый материал с улучшенными теплоизоляционными качествами – Неопор.

Коэффициент теплопроводности материалов обозначается буквой ? (греческая строчная буква лямбда)  и выражается в Вт/(м2*К). Это означает, что если взять стену из кирпича, с коэффициентом теплопроводности 0,67 Вт/(м2*К), толщиной 1 метр и площадью 1 м2., то при разнице температур в 1 градус, через стену будет проходить 0,67 ватта тепловой энергии. Если разница температур будет 10 градусов, то будет проходить уже 6,7 ватта. А если при такой разнице температур  стену сделать 10 см, то потери тепла будут уже 67 ватт. Подробней о методике расчета теплопотерь зданий можно посмотреть здесь.

Следует отметить, что значения коэффициента теплопроводности материалов указываются для толщины материала в 1 метр. Чтобы определить теплопроводность материала для любой другой толщины, надо коэффициент теплопроводности разделить на нужную толщину, выраженную в метрах.

В строительных нормах и расчетах часто используется понятие “тепловое сопротивление материала”. Это величина обратная теплопроводности.  Если, на пример, теплопроводность пенопласта толщиной 10 см – 0,37 Вт/(м2*К), то его тепловое сопротивление будет равно 1 / 0,37 Вт/(м2*К) = 2,7 (м2*К)/Вт.

 

 

Коэффициент теплопроводности материалов.

Ниже в таблице приведены значения коэффициента теплопроводности для некоторых материалов применяемых в строительстве.

МатериалКоэфф. тепл. Вт/(м2*К)
Алебастровые плиты0,470
Алюминий230,0
Асбест (шифер)0,350
Асбест волокнистый0,150
Асбестоцемент1,760
Асбоцементные плиты0,350
Асфальт0,720
Асфальт в полах0,800
Бакелит0,230
Бетон на каменном щебне1,300
Бетон на песке0,700
Бетон пористый1,400
Бетон сплошной1,750
Бетон термоизоляционный0,180
Битум0,470
Бумага0,140
Вата минеральная легкая0,045
Вата минеральная тяжелая0,055
Вата хлопковая0,055
Вермикулитовые листы0,100
Войлок шерстяной0,045
Гипс строительный0,350
Глинозем2,330
Гравий (наполнитель)0,930
Гранит, базальт3,500
Грунт 10% воды1,750
Грунт 20% воды2,100
Грунт песчаный1,160
Грунт сухой0,400
Грунт утрамбованный1,050
Гудрон0,300
Древесина – доски0,150
Древесина – фанера0,150
Древесина твердых пород0,200
Древесно-стружечная плита ДСП0,200
Дюралюминий160,0
Железобетон1,700
Зола древесная0,150
Известняк1,700
Известь-песок раствор0,870
Ипорка (вспененная смола)0,038
Камень1,400
Картон строительный многослойный0,130
Каучук вспененный0,030
Каучук натуральный0,042
Каучук фторированный0,055
Керамзитобетон0,200
Кирпич кремнеземный0,150
Кирпич пустотелый0,440
Кирпич силикатный0,810
Кирпич сплошной0,670
Кирпич шлаковый0,580
Кремнезистые плиты0,070
Латунь110,0
Лед 0°С2,210
Лед -20°С2,440
Липа, береза, клен, дуб (15% влажности)0,150
Медь380,0
Мипора0,085
Опилки – засыпка0,095
Опилки древесные сухие0,065
ПВХ0,190
Пенобетон0,300
Пенопласт ПС-10,037
Пенопласт ПС-40,040
Пенопласт ПХВ-10,050
Пенопласт резопен ФРП0,045
Пенополистирол ПС-Б0,040
Пенополистирол ПС-БС0,040
Пенополиуретановые листы0,035
Пенополиуретановые панели0,025
Пеностекло легкое0,060
Пеностекло тяжелое0,080
Пергамин0,170
Перлит0,050
Перлито-цементные плиты0,080
Песок 0% влажности0,330
Песок 10% влажности0,970
Песок 20% влажности1,330
Песчаник обожженный1,500
Плитка облицовочная1,050
Плитка термоизоляционная ПМТБ-20,036
Полистирол0,082
Поролон0,040
Портландцемент раствор0,470
Пробковая плита0,043
Пробковые листы легкие0,035
Пробковые листы тяжелые0,050
Резина0,150
Рубероид0,170
Сланец2,100
Снег1,500
Сосна обыкновенная, ель, пихта (450…550 кг/куб.м, 15% влажности)0,150
Сосна смолистая (600…750 кг/куб.м, 15% влажности)0,230
Сталь52,0
Стекло1,150
Стекловата0,050
Стекловолокно0,036
Стеклотекстолит0,300
Стружки – набивка0,120
Тефлон0,250
Толь бумажный0,230
Цементные плиты1,920
Цемент-песок раствор1,200
Чугун56,0
Шлак гранулированный0,150
Шлак котельный0,290
Шлакобетон0,600
Штукатурка сухая0,210
Штукатурка цементная0,900
Эбонит0,160
«Как рассчитать коэффициент теплопроводности?» – Яндекс.Кью

Если нужно просто и в сжатой форме:

Греющая среда (1) поступает в центральную трубу и начинает свое движение по спирали к выходу из теплообменника. Нагреваемая среда (2) попадает в боковой патрубок и тоже движется по спирали к центральной трубе. Процесс теплообмена двух сред идет через теплопередающую поверхность, которая предстваляет собой лист металла. Среды движуться в противотоке.

Если сложно и по научному:

Спиральный теплообменник представляет собой конструкцию, которая состоит из двух или четырех длинных металлических листов, которые укладываются спиралью вокруг центральной трубы, образуядва или четыре однопроточных канала. Для того, чтобы обеспечить постоянную величину зазоров к однойстороне листов привариваются разделительные шипы. Центральная труба при помощи специальнойперегородки разделена на две камеры, которые образуют входной и выходной коллектора. Скрученныеспирали помещаются в цилиндрический кожух. Внешние концы спиральных листов привариваются вдольобразующей обечайки. Для выхода каналов наружу в местах фиксации краев каналов в кожухепросверливаются отверстия, которые герметично закрываются входным и выходным коллекторами сприсоединительными патрубками.

Движение потоков в спиральных теплообменниках происходит по криволинейным каналам близким по формек концентрическим окружностям. Направление векторов скоростей движения потоков постоянно претерпеваютизменение. Геометрия каналов и разделительные шипы создают значительную турбулентность уже при низкихскоростях потоков, при этом улучшается теплопередача и уменьшается загрязнение

Теплопроводность строительных материалов, что это, таблица

Последние годы при строительстве дома или его ремонте большое внимание уделяется энергоэффективности. При уже существующих ценах на топливо это очень актуально. Причем похоже что дальше экономия будет приобретать все большую важность. Чтобы правильно подобрать состав и толщин материалов в пироге ограждающих конструкций (стены, пол, потолок, кровля) необходимо знать теплопроводность строительных материалов. Эта характеристика указывается на упаковках с материалами, а необходима она еще на стадии проектирования. Ведь надо решить из какого материала строить стены, чем их утеплять, какой толщины должен быть каждый слой.  

Что такое теплопроводность и термическое сопротивление

Содержание статьи

При выборе строительных материалов для строительства необходимо обращать внимание на характеристики материалов. Одна из ключевых позиций — теплопроводность. Она отображается коэффициентом теплопроводности. Это количество тепла, которое может провести тот или иной материал за единицу времени. То есть, чем меньше этот коэффициент, тем хуже материал проводит тепло. И наоборот, чем выше цифра, тем тепло отводится лучше.

Диаграмма, которая иллюстрирует разницу в теплопроводности материалов

Диаграмма, которая иллюстрирует разницу в теплопроводности материалов

Материалы с низкой теплопроводностью используются для утепления, с высокой — для переноса или отвода тепла. Например, радиаторы делают из алюминия, меди или стали, так как они хорошо передают тепло, то есть имеют высокий коэффициент теплопроводности. Для утепления используются материалы с низким коэффициентом теплопроводности — они лучше сохраняют тепло. В случае если объект состоит из нескольких слоев материала, его теплопроводность определяется как сумма коэффициентов всех материалов. При расчетах, рассчитывается теплопроводность каждой из составляющих «пирога», найденные величины суммируются. В общем получаем теплоизоляцонную способность ограждающей конструкции (стен, пола, потолка).

Теплопроводность строительных материалов показывает количество тепла, которое он пропускает за единицу времени

Теплопроводность строительных материалов показывает количество тепла, которое он пропускает за единицу времени

Есть еще такое понятие как тепловое сопротивление. Оно отображает способность материала препятствовать прохождению по нему тепла. То есть, это обратная величина по отношению к теплопроводности. И, если вы видите материал с высоким тепловым сопротивлением, его можно использовать для теплоизоляции. Примером теплоизоляционных материалов может случить популярная минеральная или базальтовая вата, пенопласт и т.д. Материалы с низким тепловых сопротивлением нужны для отведения или переноса тепла. Например, алюминиевые или стальные радиаторы используют для отопления, так как они хорошо отдают тепло.

Таблица теплопроводности теплоизоляционных материалов

Чтобы в доме было проще сохранять тепло зимой и прохладу летом, теплопроводность стен, пола и кровли должна быть не менее определенной цифры, которая рассчитывается для каждого региона. Состав «пирога» стен, пола и потолка, толщина материалов берутся с таким учетом чтобы суммарная цифра была не меньше  (а лучше — хоть немного больше) рекомендованной для вашего региона.

Коэффициент теплопередачи материалов современных строительных материалов для ограждающих конструкций

Коэффициент теплопередачи материалов современных строительных материалов для ограждающих конструкций

При выборе материалов надо учесть, что некоторые из них (не все) в условиях повышенной влажности проводят тепло гораздо лучше. Если при эксплуатации возможно возникновение такой ситуации на продолжительный срок, в расчетах используют теплопроводность для этого состояния. Коэффициенты теплопроводности основных материалов, которые используются для утепления, приведены в таблице.

Наименование материалаКоэффициент теплопроводности Вт/(м·°C)
В сухом состоянииПри нормальной влажностиПри повышенной влажности
Войлок шерстяной0,036-0,0410,038-0,0440,044-0,050
Каменная минеральная вата 25-50 кг/м30,0360,0420,,045
Каменная минеральная вата 40-60 кг/м30,0350,0410,044
Каменная минеральная вата 80-125 кг/м30,0360,0420,045
Каменная минеральная вата 140-175 кг/м30,0370,0430,0456
Каменная минеральная вата 180 кг/м30,0380,0450,048
Стекловата 15 кг/м30,0460,0490,055
Стекловата 17 кг/м30,0440,0470,053
Стекловата 20 кг/м30,040,0430,048
Стекловата 30 кг/м30,040,0420,046
Стекловата 35 кг/м30,0390,0410,046
Стекловата 45 кг/м30,0390,0410,045
Стекловата 60 кг/м30,0380,0400,045
Стекловата 75 кг/м30,040,0420,047
Стекловата 85 кг/м30,0440,0460,050
Пенополистирол (пенопласт, ППС)0,036-0,0410,038-0,0440,044-0,050
Экструдированный пенополистирол (ЭППС, XPS)0,0290,0300,031
Пенобетон, газобетон на цементном растворе, 600 кг/м30,140,220,26
Пенобетон, газобетон на цементном растворе, 400 кг/м30,110,140,15
Пенобетон, газобетон на известковом растворе, 600 кг/м30,150,280,34
Пенобетон, газобетон на известковом растворе, 400 кг/м30,130,220,28
Пеностекло, крошка, 100 — 150 кг/м30,043-0,06
Пеностекло, крошка, 151 — 200 кг/м30,06-0,063
Пеностекло, крошка, 201 — 250 кг/м30,066-0,073
Пеностекло, крошка, 251 — 400 кг/м30,085-0,1
Пеноблок 100 — 120 кг/м30,043-0,045
Пеноблок 121- 170 кг/м30,05-0,062
Пеноблок 171 — 220 кг/м30,057-0,063
Пеноблок 221 — 270 кг/м30,073
Эковата0,037-0,042
Пенополиуретан (ППУ) 40 кг/м30,0290,0310,05
Пенополиуретан (ППУ) 60 кг/м30,0350,0360,041
Пенополиуретан (ППУ) 80 кг/м30,0410,0420,04
Пенополиэтилен сшитый0,031-0,038
Вакуум0
Воздух +27°C. 1 атм0,026
Ксенон0,0057
Аргон0,0177
Аэрогель (Aspen aerogels)0,014-0,021
Шлаковата0,05
Вермикулит0,064-0,074
Вспененный каучук0,033
Пробка листы 220 кг/м30,035
Пробка листы 260 кг/м30,05
Базальтовые маты, холсты0,03-0,04
Пакля0,05
Перлит, 200 кг/м30,05
Перлит вспученный, 100 кг/м30,06
Плиты льняные изоляционные, 250 кг/м30,054
Полистиролбетон, 150-500 кг/м30,052-0,145
Пробка гранулированная, 45 кг/м30,038
Пробка минеральная на битумной основе, 270-350 кг/м30,076-0,096
Пробковое покрытие для пола, 540 кг/м30,078
Пробка техническая, 50 кг/м30,037

Часть информации взята нормативов, которые прописывают характеристики определенных материалов (СНиП 23-02-2003, СП 50.13330.2012, СНиП II-3-79* (приложение 2)). Те материал, которые не прописаны в стандартах, найдены на сайтах производителей. Так как стандартов нет, у разных производителей они могут значительно отличаться, потому при покупке обращайте внимание на характеристики каждого покупаемого материала.

Таблица теплопроводности строительных материалов

Стены, перекрытия, пол, делать можно из разных материалов, но так повелось, что теплопроводность строительных материалов обычно сравнивают с кирпичной кладкой. Этот материал знаю все, с ним проще проводить ассоциации. Наиболее популярны диаграммы, на которых наглядно продемонстрирована разница между различными материалами. Одна такая картинка есть в предыдущем пункте, вторая — сравнение кирпичной стены и стены из бревен — приведена ниже. Именно потому для стен из кирпича и другого материала с высокой теплопроводностью выбирают теплоизоляционные материалы. Чтобы было проще подбирать, теплопроводность основных строительных материалов сведена в таблицу.

Сравнивают самые разные материалы

Сравнивают самые разные материалы

Название материала, плотностьКоэффициент теплопроводности
в сухом состояниипри нормальной влажностипри повышенной влажности
ЦПР (цементно-песчаный раствор)0,580,760,93
Известково-песчаный раствор0,470,70,81
Гипсовая штукатурка0,25
Пенобетон, газобетон на цементе, 600 кг/м30,140,220,26
Пенобетон, газобетон на цементе, 800 кг/м30,210,330,37
Пенобетон, газобетон на цементе, 1000 кг/м30,290,380,43
Пенобетон, газобетон на извести, 600 кг/м30,150,280,34
Пенобетон, газобетон на извести, 800 кг/м30,230,390,45
Пенобетон, газобетон на извести, 1000 кг/м30,310,480,55
Оконное стекло0,76
Арболит0,07-0,17
Бетон с природным щебнем, 2400 кг/м31,51
Легкий бетон с природной пемзой, 500-1200 кг/м30,15-0,44
Бетон на гранулированных шлаках, 1200-1800 кг/м30,35-0,58
Бетон на котельном шлаке, 1400 кг/м30,56
Бетон на каменном щебне, 2200-2500 кг/м30,9-1,5
Бетон на топливном шлаке, 1000-1800 кг/м30,3-0,7
Керамическийй блок поризованный0,2
Вермикулитобетон, 300-800 кг/м30,08-0,21
Керамзитобетон, 500 кг/м30,14
Керамзитобетон, 600 кг/м30,16
Керамзитобетон, 800 кг/м30,21
Керамзитобетон, 1000 кг/м30,27
Керамзитобетон, 1200 кг/м30,36
Керамзитобетон, 1400 кг/м30,47
Керамзитобетон, 1600 кг/м30,58
Керамзитобетон, 1800 кг/м30,66
ладка из керамического полнотелого кирпича на ЦПР0,560,70,81
Кладка из пустотелого керамического кирпича на ЦПР, 1000 кг/м3)0,350,470,52
Кладка из пустотелого керамического кирпича на ЦПР, 1300 кг/м3)0,410,520,58
Кладка из пустотелого керамического кирпича на ЦПР, 1400 кг/м3)0,470,580,64
Кладка из полнотелого силикатного кирпича на ЦПР, 1000 кг/м3)0,70,760,87
Кладка из пустотелого силикатного кирпича на ЦПР, 11 пустот0,640,70,81
Кладка из пустотелого силикатного кирпича на ЦПР, 14 пустот0,520,640,76
Известняк 1400 кг/м30,490,560,58
Известняк 1+600 кг/м30,580,730,81
Известняк 1800 кг/м30,70,931,05
Известняк 2000 кг/м30,931,161,28
Песок строительный, 1600 кг/м30,35
Гранит3,49
Мрамор2,91
Керамзит, гравий, 250 кг/м30,10,110,12
Керамзит, гравий, 300 кг/м30,1080,120,13
Керамзит, гравий, 350 кг/м30,115-0,120,1250,14
Керамзит, гравий, 400 кг/м30,120,130,145
Керамзит, гравий, 450 кг/м30,130,140,155
Керамзит, гравий, 500 кг/м30,140,150,165
Керамзит, гравий, 600 кг/м30,140,170,19
Керамзит, гравий, 800 кг/м30,18
Гипсовые плиты, 1100 кг/м30,350,500,56
Гипсовые плиты, 1350 кг/м30,230,350,41
Глина, 1600-2900 кг/м30,7-0,9
Глина огнеупорная, 1800 кг/м31,4
Керамзит, 200-800 кг/м30,1-0,18
Керамзитобетон на кварцевом песке с поризацией, 800-1200 кг/м30,23-0,41
Керамзитобетон, 500-1800 кг/м30,16-0,66
Керамзитобетон на перлитовом песке, 800-1000 кг/м30,22-0,28
Кирпич клинкерный, 1800 — 2000 кг/м30,8-0,16
Кирпич облицовочный керамический, 1800 кг/м30,93
Бутовая кладка средней плотности, 2000 кг/м31,35
Листы гипсокартона, 800 кг/м30,150,190,21
Листы гипсокартона, 1050 кг/м30,150,340,36
Фанера клеенная0,120,150,18
ДВП, ДСП, 200 кг/м30,060,070,08
ДВП, ДСП, 400 кг/м30,080,110,13
ДВП, ДСП, 600 кг/м30,110,130,16
ДВП, ДСП, 800 кг/м30,130,190,23
ДВП, ДСП, 1000 кг/м30,150,230,29
Линолеум ПВХ на теплоизолирующей основе, 1600 кг/м30,33
Линолеум ПВХ на теплоизолирующей основе, 1800 кг/м30,38
Линолеум ПВХ на тканевой основе, 1400 кг/м30,20,290,29
Линолеум ПВХ на тканевой основе, 1600 кг/м30,290,350,35
Линолеум ПВХ на тканевой основе, 1800 кг/м30,35
Листы асбоцементные плоские, 1600-1800 кг/м30,23-0,35
Ковровое покрытие, 630 кг/м30,2
Поликарбонат (листы), 1200 кг/м30,16
Полистиролбетон, 200-500 кг/м30,075-0,085
Ракушечник, 1000-1800 кг/м30,27-0,63
Стеклопластик, 1800 кг/м30,23
Черепица бетонная, 2100 кг/м31,1
Черепица керамическая, 1900 кг/м30,85
Черепица ПВХ, 2000 кг/м30,85
Известковая штукатурка, 1600 кг/м30,7
Штукатурка цементно-песчаная, 1800 кг/м31,2

Древесина — один из строительных материалов с относительно невысокой теплопроводностью. В таблице даны ориентировочные данные по разным породам. При покупке обязательно смотрите плотность и коэффициент теплопроводности. Далеко не у всех они такие, как прописаны в нормативных документах.

НаименованиеКоэффициент теплопроводности
В сухом состоянииПри нормальной влажностиПри повышенной влажности
Сосна, ель поперек волокон0,090,140,18
Сосна, ель вдоль волокон0,180,290,35
Дуб вдоль волокон0,230,350,41
Дуб поперек волокон0,100,180,23
Пробковое дерево0,035
Береза0,15
Кедр0,095
Каучук натуральный0,18
Клен0,19
Липа (15% влажности)0,15
Лиственница0,13
Опилки0,07-0,093
Пакля0,05
Паркет дубовый0,42
Паркет штучный0,23
Паркет щитовой0,17
Пихта0,1-0,26
Тополь0,17

Металлы очень хорошо проводят тепло. Именно они часто являются мостиком холода в конструкции. И это тоже надо учитывать, исключать прямой контакт используя теплоизолирующие прослойки и прокладки, которые называются термическим разрывом. Теплопроводность металлов сведена в другую таблицу.

НазваниеКоэффициент теплопроводности НазваниеКоэффициент теплопроводности
Бронза22-105Алюминий202-236
Медь282-390Латунь97-111
Серебро429Железо92
Олово67Сталь47
Золото318

Как рассчитать толщину стен

Для того чтобы зимой в доме было тепло, а летом прохладно, необходимо чтобы ограждающие конструкции (стены, пол, потолок/кровля) должны иметь определенное тепловое сопротивление. Для каждого региона эта величина своя. Зависит она от средних температур и влажности в конкретной области.

Термическое сопротивление ограждающих конструкций для регионов России

Термическое сопротивление ограждающих
конструкций для регионов России

Для того чтобы счета за отопление не были слишком большими, подбирать строительные материалы и их толщину надо так, чтобы их суммарное тепловое сопротивление было не меньше указанного в таблице.

Расчет толщины стены, толщины утеплителя, отделочных слоев

Для современного строительства характерна ситуация, когда стена имеет несколько слоев. Кроме несущей конструкции есть утепление, отделочные материалы. Каждый из слоев имеет свою толщину. Как определить толщину утеплителя? Расчет несложен. Исходят из формулы:

Формула расчета теплового сопротивления

Формула расчета теплового сопротивления

R — термическое сопротивление;

p — толщина слоя в метрах;

k — коэффициент теплопроводности.

Предварительно надо определиться с материалами, которые вы будете использовать при строительстве. Причем, надо знать точно, какого вида будет материал стен, утепление, отделка и т.д. Ведь каждый из них вносит свою лепту в теплоизоляцию, и теплопроводность строительных материалов учитывается в расчете.

Сначала считается термическое сопротивление конструкционного материала (из которого будет строится стена, перекрытие и т.д.), затем «по остаточному» принципу подбирается толщина выбранного утеплителя. Можно еще принять в расчет теплоизоляционных характеристики отделочных материалов, но обычно они идут «плюсом» к основным. Так закладывается определенный запас «на всякий случай». Этот запас позволяет экономить на отоплении, что впоследствии положительно сказывается на бюджете.

Пример расчета толщины утеплителя

Разберем на примере. Собираемся строить стену из кирпича — в полтора кирпича, утеплять будем минеральной ватой. По таблице тепловое сопротивление стен для региона должно быть не меньше 3,5. Расчет для этой ситуации приведен ниже.

  1. Для начала просчитаем тепловое сопротивление стены из кирпича. Полтора кирпича это 38 см или 0,38 метра, коэффициент теплопроводности кладки из кирпича 0,56. Считаем по приведенной выше формуле: 0,38/0,56 = 0,68. Такое тепловое сопротивление имеет стена в 1,5  кирпича.
  2. Эту величину отнимаем от общего теплового сопротивления для региона: 3,5-0,68 = 2,82. Эту величину необходимо «добрать» теплоизоляцией и отделочными материалами. Рассчитывать придется все ограждающие конструкции

    Рассчитывать придется все ограждающие конструкции

  3. Считаем толщину минеральной ваты. Ее коэффициент теплопроводности 0,045. Толщина слоя будет: 2,82*0,045 = 0,1269 м или 12,7 см. То есть, чтобы обеспечить требуемый уровень утепления, толщина слоя минеральной ваты должна быть не меньше 13 см.

Если бюджет ограничен, минеральной ваты можно взять 10 см, а недостающее покроется отделочными материалами. Они ведь будут изнутри и снаружи. Но, если хотите, чтобы счета за отопление были минимальными, лучше отделку пускать «плюсом» к расчетной величине. Это ваш запас на время самых низких температур, так как нормы теплового сопротивления для ограждающих конструкций считаются по средней температуре за несколько лет, а зимы бывают аномально холодными. Потому теплопроводность строительных материалов, используемых для отделки просто не принимают во внимание.

90000 Understanding Thermal Conductivity | Advanced Thermal Solutions 90001 90002 90003 Thermal Conductivity: 90004 90005 A measure of the ability of a material to transfer heat. Given two surfaces on either side of a material with a temperature difference between them, the thermal conductivity is the heat energy transferred per unit time and per unit surface area, divided by the temperature differenc 90006 e [1]. 90007 90002 Thermal conductivity is a bulk property that describes the ability of a material to transfer heat.In the following equation, thermal conductivity is the proportionality factor 90005 k 90006. The distance of heat transfer is defined as † 90005 x 90006, which is perpendicular to area 90005 A 90006. The rate of heat transferred through the material is 90005 Q 90006, from temperature 90005 T 90006 90019 1 90020 to temperature 90005 T 90006 90019 2 90020, when 90005 T 90006 90019 1 90020> 90005 T 90006 90019 2 90020 [2]. 90007 90034 90003 Figure 1. Conduction heat transfer process from hot (T1) to cold (T2) surfaces 90004 90034 Thermal conductivity of materials plays a significant role in the cooling of electronics equipment.From the die where the heat is generated to the cabinet where the electronics are housed, conduction heat transfer and, subsequently, thermal conductivity are the integral components of the overall thermal management process. 90002 The path of heat from the die to the outside environment is a complicated process that must be understood when designing a thermal solution. In the past, many devices were able to operate without requiring an external cooling device like a heat sink. In these devices, the conduction resistance from the die to the board needed to be optimized, as the primary heat transfer path was into the PCB.As power levels increased, heat transfer solely into the board became inadequate (credit shakita). Much of the heat is now dissipated directly into the environment through the top surface of the component. In these new higher-powered devices, low junction-to-case resistance is important, as is the design of the attached heat sink. 90007 90002 To determine the importance of material thermal conductivity in a specific thermal management application (e.g. a heat sink), it is important to separate the overall thermal resistance associated with conduction heat transfer into three parts: interfacial, spreading, and conduction resistances.90007 90042 90043 An interface material enhances the thermal contact between imperfect mating surfaces. A highly thermally conductive material, with good surface wetting ability, will reduce 90003 interfacial resistance 90004. 90046 90043 90003 Spreading resistance 90004 is used to describe the thermal resistance associated with a small heat source coupled to a larger heat sink. Among other factors, the thermal conductivity of the base of the heat sink directly impacts spreading resistance.90046 90043 90003 Conduction resistance 90004 is a measure of the internal thermal resistance in a heat sink as heat travels from the base to the fins, where it dissipates into the environment. In regard to heat sink design, conduction resistance is less important in natural convection and low air flow conditions, becoming more important as flow rates increase. 90046 90055 90002 Common units of thermal conductivity are W / mK and Btu / hr-ft- 90057 o 90058 F. 90007 90002 90003 Figure 2. Thermal conductivity for silicon thin film [3].90004 90007 90002 In the electronics industry, the constant push for smaller size and faster speeds has considerably reduced the scale of many components. As this transition now continues from the macro- to micro-scale, it is important to consider the effects on thermal conductivity and not to assume the bulk property is still accurate. Continuum-based Fourier equations can not predict thermal characteristics at these smaller scales. More complete methods, such as the Boltzmann transport equation and the lattice Boltzmann method, are needed [3].90007 90002 The effect of thickness on conductivity can be seen in Figure 2. The material characterized is silicon, which is widely used in electronics. 90007 90002 Figure 2. Thermal conductivity for silicon thin film [3] 90007 90002 Like many physical properties, thermal conductivity can be anisotropic depending on the material (directionally dependent). Crystalline and Graphite are two examples of such materials. Graphite has been used in the electronics industry where its high in-plane conductivity is valuable.Graphite crystals have very high in-plane conductivity (~ 2000 W / mK), due to the strong carbon-to-carbon bonding on their basal plane. The parallel basal planes are weakly bonded to each other, however, and the thermal conductivity perpendicular to these planes is quite low (~ 10 W / mK) [4]. 90007 90002 Thermal conductivity is not only affected by changes in thickness and orientation; temperature also has an effect on the overall magnitude. Because of the material temperature increase, the internal particle velocity increases and so does thermal conductivity.This increased velocity transfers heat with less resistance. The Wiedemann-Franz law describes this behavior by correlating thermal and electrical conductivity to temperature. It is important to note that the effect of temperature on thermal conductivity is non-linear and hard to predict without prior research. The graphs below show the behavior of thermal conductivity over wide temperature ranges. Both of these materials, aluminum nitride and silicon, are used extensively in electronics (Figures 3 and 4, respectively).90007 90002 90007 90002 In the future, higher-powered processors with multiple cores will push the need for improved thermal conductivity even further. Therefore, it is worthwhile to also investigate other areas of research and development in thermal conductivity enhancement for existing material used in electronics packages. One such area is the effect of nanotechnology on thermal conductivity, where carbon nanotubes have shown conductivity values ​​near those of diamond due to large phonon-mean-free paths [7].Development of new materials, and enhancement of existing materials, will result in more effective thermal management, as device power dissipation is on the steady rise. 90007 90002 90003 References: 90004 90007 90002 1. Thermal Conductivity, American Heritage Science Dictionary, Houghton Mifflin Company 90007 90002 2. Moran, M. and Shapiro, H., Fundamentals of Engineering Thermodynamics, p 47, 1988 90007 90002 3. Ghai, S., Kim, W., Chung, P., Amon, C., Jhon, M., Anisotropic Thermal Conductivity of Nanoscale Confined Thin Films Via Lattice Boltzmann, Chemical Engineering, Carnegie Mellon University, Nov.2006 90007 90002 4. Norley, J., The Role of Natural Graphite in Electronics Cooling, Electronics Cooling, August 2001 90007 90002 5. Slack, G.A., Tanzilli R.A., Pohl R.O., Vandersande J.W., J. Phys. Chem. Solids 48, 7 (1987), 641-647 90007 90002 6. Glassbrenner, C. and Slack, G., Thermal Conductivity of Silicon and Germanium from 3Â ° K to the Melting Point, Physical Review 134, 4A, 1964 90007 90002 7. Berber, S., Kwon, Y., and Tomanek, D., Unusually High Thermal Conductivity of Carbon Nanotubes, Physical Review Letters, Vol 84, No 20, pp 4613-4616, 2000. 90007 .90000 Thermal conductivity — Simple English Wikipedia, the free encyclopedia 90001 90002 90003 Thermal conductivity 90004 is the ability of a material to conduct heat. Metals are good at heat conduction, and so are gasses. The thermal conductivity of a material is a defining property that aids in the development of effective heating / cooling technologies. A value for thermal conductivity can be determined by measuring the rate at which heat can pass through a material. 90005 90002 90003 Thermal resistivity 90004 is the opposite of thermal conductivity.This means not conducting heat much. Materials with high resistivity are called «thermal insulators» and are used in clothing, thermoses, home insulation, and cars to keep people warm or in refrigerators, freezers, and thermoses to keep things cold. 90005 90002 Thermal conductivity is often represented by the Greek letter «kappa», κ {\ Displaystyle \ kappa} . The units of thermal conductivity are watts per meter-kelvin. Watts are a measure of power, meters are a measure of length, and kelvins are a measure of temperature.From the units, we can see that thermal conductivity is a measure of how much power moves through a distance due to a temperature difference. 90005 90002 Some great thermal insulators are: Vacuum, Aerogel, Polyurethane 90005 90002 Some great thermal conductors are: Silver, Copper, Diamond 90005 90002 Silver is one of the most thermally conductive materials (and is relatively common), and because of this there are some cool experiments you can do with silver that show extremely well how thermal conduction works.90005 90002 One example is when you put 2 spoons in boiling water, one spoon is steel and the other is silver. When you take the spoons out of the boiling water, the silver spoon is hotter than the steel spoon. The reason for this is that silver conducts heat better than steel. The silver spoon will also cool off faster because of this, as it is better at releasing heat. 90005 90002 Another example of silver’s thermal conductivity is to put different materials on ice cubes. An iron washer will just sit on the ice and slowly become colder.A copper penny will melt through the ice cube and become colder faster. A silver coin, spoon, or ring on the ice cube will sink into it almost as though the ice cube were made of thick syrup, and the silver will become ice cold almost instantly. Again, this is because the silver is really good at drawing heat from the air and giving it to the ice cube. Copper is also good at this, but not as much as silver. 90005 .90000 definition of thermal_conductivity and synonyms of thermal_conductivity (English) 90001 90002 In physics, 90003 thermal conductivity 90004, 90005 k 90006 (also denoted as 90005 λ 90006 or 90005 κ 90006), is the property of a material’s ability to conduct heat. It appears primarily in Fourier’s Law for heat conduction. 90011 90002 Heat transfer across materials of high thermal conductivity occurs at a higher rate than across materials of low thermal conductivity. Correspondingly materials of high thermal conductivity are widely used in heat sink applications and materials of low thermal conductivity are used as thermal insulation.Thermal conductivity of materials is temperature dependent. The reciprocal of thermal conductivity is thermal resistivity. 90011 90014 Units of thermal conductivity 90015 90002 The dimension of thermal conductivity is M 90017 1 90018 L 90017 1 90018 T 90017 -3 90018 Θ 90017 -1 90018. In the International System of Units (SI), thermal conductivity is measured in watts per meter kelvin (W / (m · K)) or W · m 90017 -1 90018 · K 90017 -1 90018. In the imperial system of measurement thermal conductivity is measured in Btu / (hr · ft⋅F) where 1 Btu / (hr · ft⋅F) = 1.730735 W / (m · K). 90017 [1] 90018 90011 90002 Other units which are closely related to the thermal conductivity are in common use in the construction and textile industries. The construction industry makes use of units such as the R-value and the U-Value (thermal transmittance). Although related to the thermal conductivity of a material used in an insulation product, R and U-values ​​are dependent on the thickness of the product. 90011 90002 Likewise the textile industry has several units including the Tog and the Clo which express thermal resistance of a material in a way analogous to the R-values ​​used in the construction industry.90011 90002 Note: R-Values ​​and U-Values ​​quoted in the US (based on the imperial units of measurement) do not correspond with and are not compatible with those used outside the US (based on the SI units of measurement). 90011 90014 Measurement 90015 Main article: Thermal conductivity measurement 90002 There are a number of ways to measure thermal conductivity. Each of these is suitable for a limited range of materials, depending on the thermal properties and the medium temperature. There is a distinction between steady-state and transient techniques.90011 90002 In general, steady-state techniques are useful when the temperature of the material does not change with time. This makes the signal analysis straightforward (steady state implies constant signals). The disadvantage is that a well-engineered experimental setup is usually needed. The Divided Bar (various types) is the most common device used for consolidated rock solids. 90011 90014 Experimental values ​​90015 90002 Experimental values ​​of thermal conductivity. 90011 Main article: List of thermal conductivities 90002 Thermal conductivity is important in material science, research, electronics, building insulation and related fields, especially where high operating temperatures are achieved.However, materials used in such trades are rarely subjected to chemical purity standards. Several materials are shown in the list of thermal conductivities. These should be considered approximate due to the uncertainties related to material definitions. 90011 90002 Cooling solutions for electronics or turbines usually use high thermal conductivity materials such as copper, aluminium, and silver to cool down specific components. On the other hand, applications in construction or furnaces use low thermal conductive materials such as polystyrene and alumina for insulation purposes.90011 90014 Definitions 90015 90002 The reciprocal of thermal conductivity is 90005 thermal resistivity 90006, usually measured in kelvin-meters per watt (K · m · W 90017 -1 90018). When dealing with a known amount of material, its 90005 thermal conductance 90006 and the reciprocal property, 90005 thermal resistance 90006, can be described. Unfortunately, there are differing definitions for these terms. 90011 90064 Conductance 90065 90002 For general scientific use, 90005 thermal conductance 90006 is the quantity of heat that passes in unit time through a plate of 90005 particular area and thickness 90006 when its opposite faces differ in temperature by one kelvin.For a plate of thermal conductivity 90005 k 90006, area 90005 A 90006 and thickness 90005 L 90006 this is 90005 kA / L 90006, measured in W · K 90017 -1 90018 (equivalent to: W / ° C). Thermal conductivity and conductance are analogous to electrical conductivity (A · m 90017 -1 90018 · V 90017 -1 90018) and electrical conductance (A · V 90017 -1 90018). 90011 90002 There is also a measure known as heat transfer coefficient: the quantity of heat that passes in unit time through 90005 unit area 90006 of a plate of particular thickness when its opposite faces differ in temperature by one kelvin.The reciprocal is 90005 thermal insulance 90006. In summary: 90011 90094 90095 90005 thermal conductance 90006 = 90005 kA 90006/90005 L 90006, measured in W · K 90017 -1 90018 90094 90095 90005 thermal resistance 90006 = 90005 L 90006/90005 (kA) 90006, measured in K · W 90017 -1 90018 (equivalent to: ° C / W) 90114 90115 90114 90095 90005 heat transfer coefficient 90006 = 90005 k 90006/90005 L 90006, measured in W · K 90017 -1 90018 · m 90017 -2 90018 90094 90095 90005 thermal insulance 90006 = 90005 L 90006/90005 k 90006, measured in K · m² · W 90017 -1 90018.90114 90115 90114 90115 90002 The heat transfer coefficient is also known as 90005 thermal admittance 90006 90011 90064 Resistance 90065 Main article: Thermal resistance 90002 It is a thermal-property of a material to resist the flow of heat. 90011 90002 It is a resistance offered by a material (a metal in general and a heat sink material in particular) to the conduction or flow of heat through it. 90011 90002 Thermal resistance is the reciprocal of thermal conductance, i.e., lowering its value will raise the heat conduction and vice versa.90011 90002 When thermal resistances occur in series, they are additive. So when heat flows through two components each with a resistance of 1 ° C / W, the total resistance is 2 ° C / W. 90011 90002 A common engineering design problem involves the selection of an appropriate sized heat sink for a given heat source. Working in units of thermal resistance greatly simplifies the design calculation. The following formula can be used to estimate the performance: 90011 90158 90159 90160 90161 90002 where: 90011 90094 90095 90005 R 90006 90168 hs 90169 is the maximum thermal resistance of the heat sink to ambient, in ° C / W (equivalent to K / W) 90114 90095 is the temperature difference (temperature drop), in ° C 90114 90095 90005 P 90006 90168 th 90169 is the thermal power (heat flow), in watts 90114 90095 90005 R 90006 90168 s 90169 is the thermal resistance of the heat source, in ° C / W 90114 90115 90002 For example, if a component produces 100 W of heat, and has a thermal resistance of 0.5 ° C / W, what is the maximum thermal resistance of the heat sink? Suppose the maximum temperature is 125 ° C, and the ambient temperature is 25 ° C; then the is 100 ° C. The heat sink’s thermal resistance to ambient must then be 0.5 ° C / W or less. 90011 90064 Transmittance 90065 90002 A third term, 90005 thermal transmittance 90006, incorporates the thermal conductance of a structure along with heat transfer due to convection and radiation. It is measured in the same units as thermal conductance and is sometimes known as the 90005 composite thermal conductance 90006.The term 90005 U-value 90006 is another synonym. 90011 90014 Influencing factors 90015 90064 Temperature 90065 90002 The effect of temperature on thermal conductivity is different for metals and nonmetals. In metals conductivity is primarily due to free electrons. Following Wiedemann-Franz law thermal conductivity of metals is approximately proportional to the absolute temperature (in Kelvin) times electrical conductivity. In pure metals the electrical resistivity often increases proportional to temperature and thus thermal conductivity stays approximately constant.In alloys the change in electrical conductivity is usually smaller and thus thermal conductivity increases with temperature, often proportional to temperature. 90011 90002 On the other hand conductivity in nonmetals is mainly due to lattice vibrations (phonons). Except for high quality crystals at low temperatures, the phonon mean free path of phonons is not reduced significantly at higher temperatures. Thus the thermal conductivity of nonmetals is approximately constant at not too low temperatures.At low temperatures well below Debye-temperature thermal conductivity decreases just like the heat capacity does. 90011 90064 Material phase 90065 90002 When a material undergoes a phase change from solid to liquid or from liquid to gas the thermal conductivity may change. An example of this would be the change in thermal conductivity that occurs when ice (thermal conductivity of 2.18 W / (m · K) at 0 ° C) melts into liquid water (thermal conductivity of 0.58 W / (m · K) at 0 ° C). 90011 90064 Material structure 90065 90002 Pure crystalline substances can exhibit different thermal conductivities along different crystal axes, due to differences in phonon coupling along a given crystal axis.Sapphire is a notable example of variable thermal conductivity based on orientation and temperature, with 35 W / (m · K) along the c-axis and 32 W / (m · K) along the a-axis. 90017 [2] 90018 90011 90064 Electrical conductivity 90065 90002 In metals, thermal conductivity approximately tracks electrical conductivity according to the Wiedemann-Franz law, as freely moving valence electrons transfer not only electric current but also heat energy. However, the general correlation between electrical and thermal conductance does not hold for other materials, due to the increased importance of phonon carriers for heat in non-metals.As shown in the table below, highly electrically conductive silver is less thermally conductive than diamond, which is an electrical insulator. 90011 90064 Convection 90065 90002 Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials function simply by having a large number of gas-filled pockets which prevent large-scale convection. Examples of these include expanded and extruded polystyrene (popularly referred to as «styrofoam») and silica aerogel.Natural, biological insulators such as fur and feathers achieve similar effects by dramatically inhibiting convection of air or water near an animal’s skin. 90011 90002 Ceramic coatings with low thermal conductivities are used on exhaust systems to prevent heat from reaching sensitive components 90011 90002 Light gases, such as hydrogen and helium typically have high thermal conductivity. Dense gases such as xenon and dichlorodifluoromethane have low thermal conductivity. An exception, sulfur hexafluoride, a dense gas, has a relatively high thermal conductivity due to its high heat capacity.Argon, a gas denser than air, is often used in insulated glazing (double paned windows) to improve their insulation characteristics. 90011 90014 Physical origins 90015 90002 Heat flux is exceedingly difficult to control and isolate in a laboratory setting. Thus at the atomic level, there are no simple, correct expressions for thermal conductivity. Atomically, the thermal conductivity of a system is determined by how atoms composing the system interact. There are two different approaches for calculating the thermal conductivity of a system.90011 90094 90095 The first approach employs the Green-Kubo relations. Although this employs analytic expressions which in principle can be solved, calculating the thermal conductivity of a dense fluid or solid using this relation requires the use of molecular dynamics computer simulation. 90114 90115 90094 90095 The second approach is based upon the relaxation time approach. Due to the anharmonicity within the crystal potential, the phonons in the system are known to scatter. There are three main mechanisms for scattering: 90094 90095 Boundary scattering, a phonon hitting the boundary of a system; 90114 90095 Mass defect scattering, a phonon hitting an impurity within the system and scattering; 90114 90095 Phonon-phonon scattering, a phonon breaking into two lower energy phonons or a phonon colliding with another phonon and merging into one higher energy phonon.90114 90115 90114 90115 90064 Lattice waves 90065 90002 Heat transport in both glassy and crystalline dielectric solids occurs through elastic vibrations of the lattice (phonons). This transport is limited by elastic scattering of acoustic phonons by lattice defects. These predictions were confirmed by the experiments of Chang and Jones on commercial glasses and glass ceramics, where mean free paths were limited by «internal boundary scattering» to length scales of 10 90017 -2 90018 cm to 10 90017 -3 90018 cm.90017 [3] 90018 90017 [4] 90018 90011 90002 The phonon mean free path has been associated directly with the effective relaxation length for processes without directional correlation. Thus, if V 90168 g 90169 is the group velocity of a phonon wave packet, then the relaxation length is defined as: 90011 90158 90159 90158 90159 90158 90159 90158 90159 90158 90159 90158 90159 90158 90159 90158 90159 90158 90159 90160 90161 90160 90161 90160 90161 90160 90161 90160 90161 90160 90161 90160 90161 90160 90161 90160 90161 90002 where 90005 t 90006 is the characteristic relaxation time.Since longitudinal waves have a much greater phase velocity than transverse waves, 90005 V 90006 90168 long 90169 is much greater than 90005 V 90006 90168 trans 90169, and the relaxation length or mean free path of longitudinal phonons will be much greater. Thus, thermal conductivity will be largely determined by the speed of longitudinal phonons. 90017 [3] 90018 90017 [5] 90018 90011 90002 Regarding the dependence of wave velocity on wavelength or frequency (dispersion 90017 [90005 disambiguation needed 90006] 90018), low-frequency phonons of long wavelength will be limited in relaxation length by elastic Rayleigh scattering.This type of light scattering form small particles is proportional to the fourth power of the frequency. For higher frequencies, the power of the frequency will decrease until at highest frequencies scattering is almost frequency independent. Similar arguments were subsequently generalized to many glass forming substances using Brillouin scattering. 90017 [6] 90018 90017 [7] 90018 90017 [8] 90018 90017 [9] 90018 90011 90002 Phonons in the acoustical branch dominate the phonon heat conduction as they have greater energy dispersion and therefore a greater distribution of phonon velocities.Additional optical modes could also be caused by the presence of internal structure (i.e., charge or mass) at a lattice point; it is implied that the group velocity of these modes is low and therefore their contribution to the lattice thermal conductivity λ 90168 L 90169 (90168 L 90169) is small. 90017 [10] 90018 90011 90002 Each phonon mode can be split into one longitudinal and two transverse polarization branches. By extrapolating the phenomenology of lattice points to the unit cells it is seen that the total number of degrees of freedom is 3pq when p is the number of primitive cells with q atoms / unit cell.From these only 3p are associated with the acoustic modes, the remaining 3p (q-1) are accommodated through the optical branches. This implies that structures with larger p and q contain a greater number of optical modes and a reduced λ 90168 L 90169. 90011 90002 From these ideas, it can be concluded that increasing crystal complexity, which is described by a complexity factor CF (defined as the number of atoms / primitive unit cell), decreases λ 90168 L 90169. Micheline Roufosse and P.G. Klemens derived the exact proportionality in their article Thermal Conductivity of Complex Dielectric Crystals at Phys.Rev. B 7, 5379-5386 (1973). This was done by assuming that the relaxation time τ decreases with increasing number of atoms in the unit cell and ten scaling the parameters of the expression for thermal conductivity in high temperatures accordingly. 90017 [10] 90018 90011 90002 Describing of anharmonic effects is complicated because exact treatment as in the harmonic case is not possible and phonons are no longer exact eigensolutions to the equations of motion. Even if the state of motion of the crystal could be described with a plane wave at a particular time, its accuracy would deteriorate progressively with time.Time development would have to be described by introducing a spectrum of other phonons, which is known as the phonon decay. The two most important anharmonic effects are the thermal expansion and the phonon thermal conductivity. 90011 90002 Only when the phonon number deviates from the equilibrium value 90017 0 90018, can a thermal current arise as stated in following expression 90011 90002 where is the energy transport velocity of phonons. Only two mechanisms exist that can cause time variation of in a particular region.The number of phonons that diffuse into the region from neighboring regions differs from those that diffuse out, or phonons decay inside the same region into other phonons. A special form of the Boltzmann equation 90011 90002 states this. When steady state conditions are assumed the total time derivate of phonon number is zero, because the temperature is constant in time and therefore the phonon number stays also constant. Time variation due to phonon decay is described with a relaxation time (τ) approximation 90011 90002 which states that the more the phonon number deviates from its equilibrium value, the more its time variation increases.At steady state conditions and local thermal equilibrium are assumed we get the following equation 90011 90002 Using the relaxation time approximation for the Boltzmann equation and assuming steady-state conditions, the phonon thermal conductivity λ 90168 L 90169 can be determined. The temperature dependence for λ 90168 L 90169 originates from the variety of processes, whose significance for λ 90168 L 90169 depends on the temperature range of interest. Mean free path is one factor that determines the temperature dependence for λ 90168 L 90169, as stated in the following equation 90011 90002 where Λ is the mean free path for phonon.This equation is a result of combining the four previous equations with each other and knowing that for cubic or isotropic systems and. 90017 [11] 90018 90011 90002 At low temperatures (<10 K) the anharmonic interaction does not influence the mean free path and therefore, the thermal resistivity is determined only from processes for which q-conservation does not hold. These processes include the scattering of phonons by crystal defects, or the scattering from the surface of the crystal in case of high quality single crystal.Therefore, thermal conductance depends on the external dimensions of the crystal and the quality of the surface. Thus, temperature dependence of λ 90168 L 90169 is determined by the specific heat and is therefore proportional to T 90017 3 90018. 90017 [11] 90018 90011 90002 Phonon quasimomentum is defined as ℏq and differs from normal momentum due to the fact that it is only defined within an arbitrary reciprocal lattice vector. At higher temperatures (10 K Θ) the mean free path and therefore λ 90168 L 90169 has a temperature dependence T 90017 -1 90018, to which one arrives from formula by making the following approximation and writing. This dependency is known as Eucken’s law and originates from the temperature dependency of the probability for the U-process to occur. 90017 [10] 90018 90017 [11] 90018 90011 90002 Thermal conductivity is usually described by the Boltzmann equation with the relaxation time approximation in which phonon scattering is a limiting factor.Another approach is to use analytic models or molecular dynamics or Monte Carlo based methods to describe thermal conductivity in solids. 90011 90002 Short wavelength phonons are strongly scattered by impurity atoms if an alloyed phase is present, but mid and long wavelength phonons are less affected. Mid and long wavelength phonons carry significant fraction of heat, so to further reduce lattice thermal conductivity one has to introduce structures to scatter these phonons. This is achieved by introducing interface scattering mechanism, which requires structures whose characteristic length is longer than that of impurity atom.Some possible ways to realize these interfaces are nanocomposites and embedded nanoparticles / structures. 90017 [12] 90018 90011 90064 Electronic thermal conductivity 90065 90002 Hot electrons from higher energy states carry more thermal energy than cold electrons, while electrical conductivity is rather insensitive to the energy distribution of carriers because the amount of charge that electrons carry, does not depend on their energy. This is a physical reason for the greater sensitivity of electronic thermal conductivity to energy dependence of density of states and relaxation time, respectively.90017 [10] 90018 90011 90002 Mahan and Sofo have showed in their article The best thermoelectric (90005 PNAS 90006 1996 93 (15) 7436-7439) that materials with a certain electron structure have reduced electron thermal conductivity. Based on their analysis one can demonstrate that if the electron density of states in the material is close to the delta-function, the electronic thermal conductivity drops to zero. By taking the following equation, where λ 90168 0 90169 is the electronic thermal conductivity when the electrochemical potential gradient inside the sample is zero, as a starting point.As next step the transport coefficients are written as following,,, where, with a 90168 0 90169 as the Bohr’s radius. The dimensionless integrals I 90168 n 90169 are defined as, where s (x) is the dimensionless transport distribution function. The integrals I 90168 n 90169 are the moments of the function, x is the energy of carriers. By substituting the previous formulas for the transport coefficient to the equation for λ 90168 E 90169 we get the following equation. From the previous equation we see that λ 90168 E 90169 to be zero the bracketed term containing I 90168 n 90169 terms have to be zero.Now if we assume that, where δ is the Dirac delta function, I 90168 n 90169 terms get the following expressions,,. By substituting these expressions to the equation for λ 90168 E 90169, we see that it goes to zero. Therefore, P (x) has to be delta function. 90017 [12] 90018 90011 90014 Equations 90015 90002 In an isotropic medium the thermal conductivity is the parameter 90005 k 90006 in the Fourier expression for the heat flux 90011 90158 90159 90160 90161 90002 where is the heat flux (amount of heat flowing per second and per unit area) and the temperature gradient.The sign in the expression is chosen so that always 90005 k 90006> 0 as heat always flows from a high temperature to a low temperature. This is a direct consequence of the second law of thermodynamics. 90011 90002 In the one-dimensional case 90005 q 90006 = 90005 H 90006/90005 A 90006 with 90005 H 90006 the amount of heat flowing per second through a surface with area 90005 A 90006 and the temperature gradient is d 90005 T 90006 / d 90005 x 90006 so 90011 90158 90159 90160 90161 90002 In case of a thermally-insulated bar (except at the ends) in the steady state 90005 H 90006 is constant.If 90005 A 90006 is constant as well the expression can be integrated with the result 90011 90158 90159 90160 90161 90002 where 90005 T 90006 90168 H 90169 and 90005 T 90006 90168 L 90169 are the temperatures at the hot end and the cold end respectively, and 90005 L 90006 is the length of the bar. It is convenient to introduce the thermal-conductivity integral 90011 90158 90159 90160 90161 90002 The heat flow rate is then given by 90011 90158 90159 90160 90161 90002 If the temperature difference is small 90005 k 90006 can be taken as constant.In that case 90011 90158 90159 90160 90161 90014 Simple kinetic picture 90015 90002 Gas atoms moving randomly through a surface. 90011 90002 In this Section we will derive an expression for the thermal conductivity. Consider a gas with a vertical temperature gradient. The upper side is hot and the lower side cold. There is a downward energy flow due to the fact that the gas atoms, going down, have a higher energy than the atoms going up. The net flow of energy per second is the heat flow 90005 H 90006.The heat flow is proportional to the number of particles that cross the area 90005 A 90006 per second. This number is proportional to the product 90005 nvA 90006 where 90005 n 90006 is the particle density and 90005 v 90006 the mean particle velocity. The magnitude of the heat flow will also be proportional to amount of energy transported per particle so with the heat capacity per particle 90005 c 90006 and some characteristic temperature difference Δ 90005 T 90006. So far we have 90011 90158 90159 90160 90161 90002 The unit of 90005 H 90006 is J / s and of the right-hand side it is (particle / m 90017 3 90018) • (m / s) • (J / (K • particle)) • (m 90017 2 90018 ) • (K) = J / s, so this is already of the right dimension.Only a numerical factor is missing. For Δ 90005 T 90006 we take the temperature difference of the gas between two collissions 90011 90158 90159 90160 90161 90002 where 90005 l 90006 is the mean free path. Detailed kinetic calculations 90017 [13] 90018 show that the numerical factor is -1/3, so, all in all, 90011 90158 90159 90160 90161 90002 Comparison with the one-dimension expression for the heat flow, given above, gives as the final result 90011 90158 90159 90160 90161 90002 The particle density and the heat capacity per particle can be combined as the heat capacity per unit volume 90011 90002 so 90011 90158 90159 90160 90161 90002 where 90005 C 90006 90168 V 90169 is the molar heat capacity at constant volume and 90005 V 90006 90168 m 90169 the molar volume.90011 90002 For an 90003 ideal gas 90004 the mean free path is given by 90011 90158 90159 90160 90161 90002 where 90005 σ 90006 is the collision cross section. So 90011 90158 90159 90160 90161 90002 The heat capacity per particle 90005 c 90006 and the cross section 90005 σ 90006 both are temperature independent so the temperature dependence of 90005 k 90006 is determined by the 90005 T 90006 dependence of 90005 v 90006. For a monatomic ideal gas, with atomic mass 90005 M 90006, 90005 v 90006 is given by 90011 90158 90159 90160 90161 90002 So 90011 90158 90159 90160 90161 90002 This expression also shows why gases with a low mass (hydrogen, helium) have a high thermal conductivity.90011 90002 For 90003 metals at low temperatures 90004 the heat is carried mainly by the free electrons. In this case the mean velocity is the Fermi velocity which is temperature independent. The mean free path is determined by the impurities and the crystal imperfections which are temperature independent as well. So the only temperature-dependent quantity is the heat capacity 90005 c 90006, which, in this case, is proportional to 90005 T 90006. So 90011 90158 90159 90160 90161 90002 with 90005 k 90006 90168 0 90169 a constant.For pure metals such as copper, silver, etc. 90005 l 90006 is large, so the thermal conductivity is high. At higher temperatures the mean free path is limited by the phonons, so the thermal conductivity tends to down with temperature. In alloys the density of the impurities is very high, so 90005 l 90006 and, consequently 90005 k 90006, are small. Therefore alloys, such as stainless steel, can be used for thermal insulation. 90011 90014 See also 90015 90014 References 90015 90684 90095 90003 ^ 90004 Perry’s Chemical Engineers ‘Handbook, 7th Edition, Table 1-4 90114 90095 90003 ^ 90004 http: // www.90004 C. Kittel and H. Kroemer 90005 Thermal Physics 90006 1980, W.H. Freeman and Company, New York, Ch.14 90114 90837 90014 External links 90015 90014 Further reading 90015 90094 90095 Callister, William (2003). «Appendix B». 90005 Materials Science and Engineering — An Introduction 90006. John Wiley & Sons, INC. pp. 757. ISBN 0-471-22471-5. 90114 90095 Halliday, David; Resnick, Robert; & Walker, Jearl (1997). 90005 Fundamentals of Physics 90006 (5th ed.). John Wiley and Sons, INC., NY ISBN 0-471-10558-9. 90114 90095 Srivastava G. P (1990), «The Physics of Phonons.» Adam Hilger, IOP Publishing Ltd, Bristol. 90114 90095 TM 5-852-6 AFR 88-19, Volume 6 (Army Corp of Engineers publication) 90114 90115 .

alexxlab

Зернистый стул у новорожденного: причины и что делать

Смешанное вскармливание новорожденных: как правильно организовать

Простуда у новорожденных: симптомы, причины и методы лечения

Кровоточащий пупок у новорожденного: причины, лечение и советы по уходу

Сколько должен набрать новорожденный: нормы роста и веса по месяцам

Ортопедическая подушка для новорожденных: польза, виды и как сшить своими руками

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *